librosa是一个应用广泛的音频处理python库。

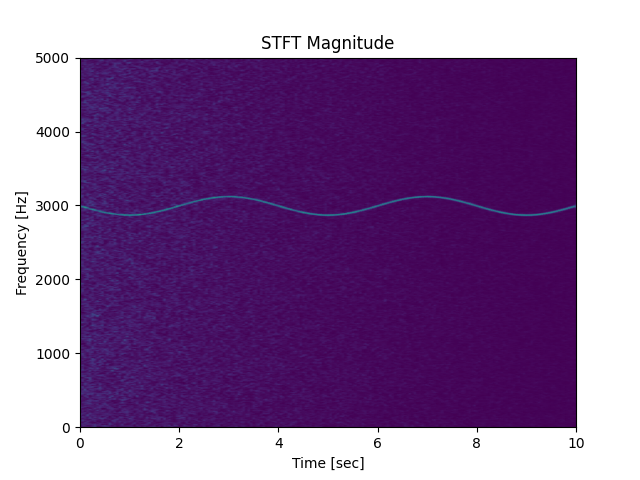
在librosa中有一个方法叫做stft，功能是求音频的短时傅里叶变换, librosa.stft 返回是一个矩阵

短时傅立叶变换（STFT），返回一个复数矩阵使得D(f,t)

1. 当调用的形式是 np.abs( stft() ), 代表的是取， 取出复数矩阵的实部，即频率的振幅。

2. 当调用的形式是 np.angle( stft() ), 代表的是取， 取出复数矩阵的虚部，即频率的相位。

This function returns a complex-valued matrix D such that
- np.abs(D[f, t]) is the magnitude of frequency bin f
at frame t, and
- np.angle(D[f, t]) is the phase of frequency bin f
at frame t.

The integers t and f can be converted to physical units by means
of the utility functions frames_to_sample and fft_frequencies.

1. librosa.stft函数

librosa.stft(y, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')

参数：

• y：音频时间序列

• n_fft：FFT窗口大小，n_fft=hop_length+overlapping

• hop_length：帧移，如果未指定，则默认win_length / 4。

• win_length：每一帧音频都由window（）加窗。窗长win_length，然后用零填充以匹配N_FFT。默认win_length=n_fft。

• window：字符串，元组，数字，函数 shape =（n_fft, )
  窗口（字符串，元组或数字）；
  窗函数，例如scipy.signal.hanning
  长度为n_fft的向量或数组

• center：bool
  如果为True，则填充信号y，以使帧 D [:, t]以y [t * hop_length]为中心。
  如果为False，则D [:, t]从y [t * hop_length]开始

• dtype：D的复数值类型。默认值为64-bit complex复数

• pad_mode：如果center = True，则在信号的边缘使用填充模式。默认情况下，STFT使用reflection padding。

返回：
STFT矩阵，shape = (1+ $\frac{n_{fft}}{2}$, $n_{frames}$ )

2. stft的输出帧数

音频短时傅里叶变换后，在对音频取幅值，可以得到音频的线性谱。

对线性谱进行mel刻度的加权求和，可以得到语音识别和语音合成中常用的mel谱。

短时傅里叶变换的过程是先对音频分帧，再分别对每一帧傅里叶变换。

在应用stft方法求解短时傅里叶变换时，发现求出的特征帧的数目有点反常。

比如我有一个长度是400个点的音频，如果帧长是100，那么我自然而然的想到，最后应当得到4帧。

但实际不是这个样子的，实际的帧数为5帧。这就有点神奇了。

分析了一下，原因如下。

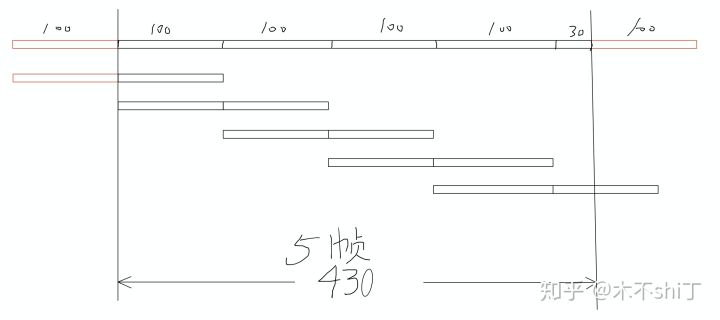
为了方便讨论，假设帧长为200，帧移为100，fft size是200。

上图中是一条长度为430的音频，在经过stft后，输出5帧。

过程是这样的。

1. 在音频的左右两侧padding，padding size是fft size的一半

2. 现在音频长度变成了430 + 200 = 630

3. 总帧数为(630 - 100) // 100

4. 如上图示意，最后得到5帧

所以，librosa求stft的输出帧数，当音频长度在400 <= x < 500之间时，输出帧数为5。

推广开来，音频求stft的输出帧数都是 audio_length // hop_length + 1。

这个东西有什么用呢？在用到帧和原始采样点相对应的场景下，千万别忘了padding 0 到帧数那么多，再去进行其他操作。

如果有兴趣可以写代码自己验证一下。

3. 　各个参数的分析

n_fftFFT点数，也是补零后每一帧信号的长度。输出的行数与n_fft有关，为n_fft/2+1

hop_length帧移。可以理解为下一帧相对上一帧移动了多少个采样点。使用更小的值可以在不减少频率分辨率的情况下增加输出的列数。默认是win_length/4

win_length窗长。使用该长度的窗函数截取语音后得到每一帧信号。更小的值会在牺牲STFT频率分辨率的同时增加其时间分辨率

center默认为Ture，即在原信号r的左右两边分别补上n_fft//2个点，使得第t帧的信号以r[thop_length]为中心点。当为False时，第t帧的信号以r[thop_length]为起点

pad_mode默认为”reflect”，即在center=True时，采用镜像模式对r进行填补，比如[1, 2, 3, 4]会被补为[3, 2, 1, 2, 3, 4, 3 ,2]

3.1 时频分辨率

时间分辨率：

liborsa中，时间分辨率(Temporal Resolution)的解释为：在时域中分辨出紧邻的冲击的能力。

频率分辨率：

频率分辨率(Frequency Resolution)的解释为：在频域中分辨出紧邻的单频率音的能力。

与二者相关的参数分别是win_length和n_fft，表现为win_length越小，时间分辨率越精准；n_fft越大，频率分辨率越精准。

但是，在实际中，不能只按照win_length <= n_fft来选取它们。

在实际操作中，当每帧长度不等于FFT点数时，要将窗函数的两边同时补零到n_fft长度且对每帧数据加窗（参考librosa和torch.stft()的）后，才能进行FFT。

但这不并不是说因为会自动补零，就可以随便选取win_length。

3.2 如何提升分辨率

(T)为原始数据的时长，${\mathbb{N}}_{fft}$为FFT点数。当(T)不变时，不论如何提升${\mathbb{N}}_{fft}$，都不能提高波形频率分辨率(\Delta R_w)。

对此的解释是：“在时域或频域内补零，只能提升另一个域内的插值密度(Interpolation-density)，而非提升分辨率。”

为了提升FFT分辨率，我们要收集更多的原始数据，做点数更大的FFT.

要提升频率分辨率，必须同时增大每帧数据的长度win_length和FFT点数n_fft.

注意，　这里的每帧的数据长度　win_length, 指的是没有通过补零得到的原始数据。

3.3 帧移长度的选取

既然win_length和n_fft的值都不能随便选，那么hop_length…

没错，在选择窗函数和帧移时，必须要满足Constant Overlap-Add(COLA):

$$\begin{array}{c}\sum _{m=-\infty }^{\infty }w(n-mR)=1,\forall n\in \mathbb{Z}\end{array}\text{\hspace{1em}(3)}$$

COLA确保了输入中的每个点都有同样的权值，从而避免出现时域混叠(aliasing)，以及确保ISTFT能够完美地重构原信号。这是因为，在对语音进行分帧加窗时，每帧之间存在重叠的部分，且该部分在ISTFT后也会存在。

比如使用矩形窗就不能完美地重构原信号。

在STFT中常用的$\frac{1}{2}$ 、$\frac{2}{3}$、$\frac{1}{4}$重叠率的汉宁窗符合COLA。

窗函数和帧移的选取并不是随意的。

默认center=Ture,要在原数据左右两端补上$\frac{N_{fft}}{2}$个点，人为地让原始语音在能够完美重构信号的范围内。

4. code

@cache(level=20)
def stft(y,n_fft=2048,hop_length=None,win_length=None,window="hann",center=True,dtype=None,pad_mode="reflect",
):"""Short-time Fourier transform (STFT).The STFT represents a signal in the time-frequency domain bycomputing discrete Fourier transforms (DFT) over short overlappingwindows.This function returns a complex-valued matrix D such that- ``np.abs(D[f, t])`` is the magnitude of frequency bin ``f``at frame ``t``, and- ``np.angle(D[f, t])`` is the phase of frequency bin ``f``at frame ``t``.The integers ``t`` and ``f`` can be converted to physical units by meansof the utility functions `frames_to_sample` and `fft_frequencies`.Parameters----------y : np.ndarray [shape=(n,)], real-valuedinput signaln_fft : int > 0 [scalar]length of the windowed signal after padding with zeros.The number of rows in the STFT matrix ``D`` is ``(1 + n_fft/2)``.The default value, ``n_fft=2048`` samples, corresponds to a physicalduration of 93 milliseconds at a sample rate of 22050 Hz, i.e. thedefault sample rate in librosa. This value is well adapted for musicsignals. However, in speech processing, the recommended value is 512,corresponding to 23 milliseconds at a sample rate of 22050 Hz.In any case, we recommend setting ``n_fft`` to a power of two foroptimizing the speed of the fast Fourier transform (FFT) algorithm.hop_length : int > 0 [scalar]number of audio samples between adjacent STFT columns.Smaller values increase the number of columns in ``D`` withoutaffecting the frequency resolution of the STFT.If unspecified, defaults to ``win_length // 4`` (see below).win_length : int <= n_fft [scalar]Each frame of audio is windowed by ``window`` of length ``win_length``and then padded with zeros to match ``n_fft``.Smaller values improve the temporal resolution of the STFT (i.e. theability to discriminate impulses that are closely spaced in time)at the expense of frequency resolution (i.e. the ability to discriminatepure tones that are closely spaced in frequency). This effect is knownas the time-frequency localization trade-off and needs to be adjustedaccording to the properties of the input signal ``y``.If unspecified, defaults to ``win_length = n_fft``.window : string, tuple, number, function, or np.ndarray [shape=(n_fft,)]Either:- a window specification (string, tuple, or number);see `scipy.signal.get_window`- a window function, such as `scipy.signal.windows.hann`- a vector or array of length ``n_fft``Defaults to a raised cosine window (`'hann'`), which is adequate formost applications in audio signal processing... see also:: `filters.get_window`center : booleanIf ``True``, the signal ``y`` is padded so that frame``D[:, t]`` is centered at ``y[t * hop_length]``.If ``False``, then ``D[:, t]`` begins at ``y[t * hop_length]``.Defaults to ``True``,  which simplifies the alignment of ``D`` onto atime grid by means of `librosa.frames_to_samples`.Note, however, that ``center`` must be set to `False` when analyzingsignals with `librosa.stream`... see also:: `librosa.stream`dtype : np.dtype, optionalComplex numeric type for ``D``.  Default is inferred to match theprecision of the input signal.pad_mode : string or functionIf ``center=True``, this argument is passed to `np.pad` for paddingthe edges of the signal ``y``. By default (``pad_mode="reflect"``),``y`` is padded on both sides with its own reflection, mirrored aroundits first and last sample respectively.If ``center=False``,  this argument is ignored... see also:: `numpy.pad`Returns-------D : np.ndarray [shape=(1 + n_fft/2, n_frames), dtype=dtype]Complex-valued matrix of short-term Fourier transformcoefficients.See Also--------istft : Inverse STFTreassigned_spectrogram : Time-frequency reassigned spectrogramNotes-----This function caches at level 20.Examples-------->>> y, sr = librosa.load(librosa.ex('trumpet'))>>> S = np.abs(librosa.stft(y))>>> Sarray([[5.395e-03, 3.332e-03, ..., 9.862e-07, 1.201e-05],[3.244e-03, 2.690e-03, ..., 9.536e-07, 1.201e-05],...,[7.523e-05, 3.722e-05, ..., 1.188e-04, 1.031e-03],[7.640e-05, 3.944e-05, ..., 5.180e-04, 1.346e-03]],dtype=float32)Use left-aligned frames, instead of centered frames>>> S_left = librosa.stft(y, center=False)Use a shorter hop length>>> D_short = librosa.stft(y, hop_length=64)Display a spectrogram>>> import matplotlib.pyplot as plt>>> fig, ax = plt.subplots()>>> img = librosa.display.specshow(librosa.amplitude_to_db(S,...                                                        ref=np.max),...                                y_axis='log', x_axis='time', ax=ax)>>> ax.set_title('Power spectrogram')>>> fig.colorbar(img, ax=ax, format="%+2.0f dB")"""# By default, use the entire frameif win_length is None:win_length = n_fft# Set the default hop, if it's not already specifiedif hop_length is None:hop_length = int(win_length // 4)fft_window = get_window(window, win_length, fftbins=True)# Pad the window out to n_fft sizefft_window = util.pad_center(fft_window, n_fft)# Reshape so that the window can be broadcastfft_window = fft_window.reshape((-1, 1))# Check audio is validutil.valid_audio(y)# Pad the time series so that frames are centeredif center:if n_fft > y.shape[-1]:warnings.warn("n_fft={} is too small for input signal of length={}".format(n_fft, y.shape[-1]))y = np.pad(y, int(n_fft // 2), mode=pad_mode)elif n_fft > y.shape[-1]:raise ParameterError("n_fft={} is too large for input signal of length={}".format(n_fft, y.shape[-1]))# Window the time series.y_frames = util.frame(y, frame_length=n_fft, hop_length=hop_length)if dtype is None:dtype = util.dtype_r2c(y.dtype)# Pre-allocate the STFT matrixstft_matrix = np.empty((int(1 + n_fft // 2), y_frames.shape[1]), dtype=dtype, order="F")fft = get_fftlib()# how many columns can we fit within MAX_MEM_BLOCK?n_columns = util.MAX_MEM_BLOCK // (stft_matrix.shape[0] * stft_matrix.itemsize)n_columns = max(n_columns, 1)for bl_s in range(0, stft_matrix.shape[1], n_columns):bl_t = min(bl_s + n_columns, stft_matrix.shape[1])stft_matrix[:, bl_s:bl_t] = fft.rfft(fft_window * y_frames[:, bl_s:bl_t], axis=0)return stft_matrix

参考：
参考文章