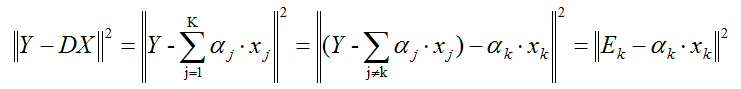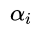• 字典学习也是一种数据降维的方法，这里我用到SVD的知识，对SVD不太理解的地方，可以看看这篇博客： 奇异值分解SVD
  

一、字典学习数学模型

字典学习的思想应该源来实际生活中的字典的概念。字典是前辈们学习总结的精华，当我们需要学习新的知识的时候，不必与先辈们一样去学习先辈们所有学习过的知识，我们可以参考先辈们给我们总结的字典，通过查阅这些字典，我们可以大致学会到这些知识。为了将上述过程用准确的数学语言描述出来，我们需要将“总结字典”、“查阅字典”做出一个更为准确的描述。就从我们的常识出发：

• 1.我们通常会要求的我们的字典尽可能全面，也就是说总结出的字典不能漏下关键的知识点。
• 2.查字典的时候，我们想要我们查字典的过程尽可能简洁，迅速，准确。即，查字典要快、准、狠。
• 3.查到的结果，要尽可能地还原出原来知识。当然，如果要完全还原出来，那么这个字典和查字典的方法会变得非常复杂，所以我们只需要尽可能地还原出原知识点即可。

下面，我们要讨论的就是如何将上述问题抽象成一个数学问题，并解决这个问题。

1.1、数学描述

我们将上面的所提到的关键点用几个数学符号表示一下：

• “以前的知识”，更专业一点，我们称之为原始样本，用矩阵$\mathbf{Y}$表示；
• “字典”，我们称之为字典矩阵，用$\mathbf{D}$表示，“字典”中的词条，我们称之为原子（atom），用列向量 ${\mathbf{d}}_{\mathbf{k}}$ 表示；
• “查字典的方法”，我们称为稀疏矩阵，用 $\mathbf{X}$；
• “查字典的过程”，我们可以用矩阵的乘法来表示，即 $\mathbf{D}\mathbf{X}$。

• 用数学语言描述，字典学习的主要思想是，利用包含 $K$ 个原子 ${\mathbf{d}}_{\mathbf{k}}$的字典矩阵$\mathbf{D}\in {\mathbf{R}}^{m\times K}$，稀疏线性表示原始样本$\mathbf{Y}\in {\mathbf{R}}^{m\times n}$（其中 $n$ 表示样本数，$m$ 表示样本的属性），即有$\mathbf{Y}=\mathbf{D}\mathbf{X}$（这只是我们理想的情况），其中$\mathbf{X}\in {\mathbf{R}}^{K\times n}$为稀疏矩阵，可以将上述问题用数学语言描述为如下优化问题:
  $$\underset{\mathbf{D},\mathbf{X}}{\min }\Vert \mathbf{Y}-\mathbf{D}\mathbf{X}{\Vert }_F^2,\text{s.t.}\forall i,\Vert {\mathbf{x}}_i{\Vert }_0\le T_0\text{\hspace{1em}(1-1)}$$
• 或者
  $$\underset{\mathbf{D},\mathbf{X}}{\min }\sum _i\Vert {\mathbf{x}}_i{\Vert }_0,\text{s.t.}\underset{\mathbf{D},\mathbf{X}}{\min }\Vert \mathbf{Y}-\mathbf{D}\mathbf{X}{\Vert }_F^2\le ϵ,\text{\hspace{1em}(1-2)}$$
• 上式中 $\mathbf{X}$ 为稀疏编码的矩阵， ${\mathbf{x}}_i(i=1,2,\cdots ,K)$，为该矩阵中的行向量，代表字典矩阵的系数。
• 注意：$\Vert {\mathbf{x}}_{\mathbf{i}}{\Vert }_0$表示零阶范数，它表示向量中不为0的数的个数。即是想让其尽可能的稀疏，非0的元素尽可能的少。

1.2、求解问题

• 式（1-1）的目标函数表示，我们要最小化查完的字典与原始样本的误差，即要尽可能还原出原始样本；它的限的制条件 $\Vert {\mathbf{x}}_i{\Vert }_0\le T_0$，，表示查字典的方式要尽可能简单，即$X$要尽可能稀疏。式（1-2）同理。式（1-1）或式（1-2）是一个带有约束的优化问题，可以利用拉格朗日乘子法将其转化为无约束优化问题
  $$\underset{\mathbf{D},\mathbf{X}}{\min }\Vert \mathbf{Y}-\mathbf{D}\mathbf{X}{\Vert }_F^2+\lambda \Vert {\mathbf{x}}_i{\Vert }_1\text{\hspace{1em}(1-3)}$$
• 注意： $\Vert {\mathbf{x}}_{\mathbf{i}}{\Vert }_0$表示零阶范数 我们将$\Vert {\mathbf{x}}_{\mathbf{i}}{\Vert }_0$用$\Vert {\mathbf{x}}_{\mathbf{i}}{\Vert }_1$代替，主要是$\Vert {\mathbf{x}}_{\mathbf{i}}{\Vert }_1$更加便于求解。

• 这里有两个优化变量$\mathbf{D},\mathbf{X}$，为解决这个优化问题，一般是固定其中一个优化变量，优化另一个变量，如此交替进行。式（1-3）中的稀疏矩阵$\mathbf{X}$可以利用已有经典算法求解，如Lasso（Least Absolute Shrinkage and Selection Operator）、OMP（Orthogonal Matching Pursuit），这里我重点讲述如何更新字典$\mathbf{D}$，对更新$\mathbf{X}$不多做讨论。
• 假设$\mathbf{X}$是已知的，我们逐列更新字典。下面我们仅更新字典的第$k$列，记${\mathbf{d}}_{\mathbf{k}}$ 为字典$\mathbf{D}$的第$k$列向量，记 ${\mathbf{x}}_T^k$ 为稀疏矩阵$\mathbf{X}$的第 $k$ 行向量，那么对式（1-1），我们有:
  $$\begin{array}{rl}\Vert \mathbf{Y}-\mathbf{D}\mathbf{X}{\Vert }_F^2=& {\Vert \mathbf{Y}-\sum _{j=1}^K{\mathbf{d}}_j{\mathbf{x}}_T^j\Vert }_F^2\\ =& {\Vert \left(\mathbf{Y}-\sum _{j\ne k}{\mathbf{d}}_j{\mathbf{x}}_T^j\right)-{\mathbf{d}}_k{\mathbf{x}}_T^k\Vert }_F^2\\ =& {\Vert {\mathbf{E}}_k-{\mathbf{d}}_k{\mathbf{x}}_T^k\Vert }_F^2\end{array}\text{\hspace{1em}(1-4)}$$
• 上式中残差: $${\mathbf{E}}_k=\mathbf{Y}-\sum _{j\ne k}{\mathbf{d}}_j{\mathbf{x}}_T^j\text{\hspace{1em}(1-5)}$$
• 此时优化问题可描述为: $$\underset{{\mathbf{d}}_k,{\mathbf{x}}_T^k}{\min }{\Vert {\mathbf{E}}_k-{\mathbf{d}}_k{\mathbf{x}}_T^k\Vert }_F^2\text{\hspace{1em}(1-6)}$$
• 因此我们需要求出最优的 ${\mathbf{d}}_k,{\mathbf{x}}_T^k$，这是一个最小二乘问题，可以利用最小二乘的方法求解，或者可以利用SVD进行求解，这里利用SVD的方式求解出两个优化变量。

• 但是，在这里我人需要注意的是，不能直接利用 ${\mathbf{E}}_k$ 进行求解，否则求得的新的 ${\mathbf{x}}_T^k$ 不稀疏。因此我们需要将 ${\mathbf{E}}_k$中对应的${\mathbf{x}}_T^k$不为0的位置提取出来，得到新的${\mathbf{E}}_k^{{}^{\prime }}$，这个过程如图2-1所示，这样描述更加清晰。
  
• 如上图，假设我们要更新第0列原子，我们将${\mathbf{x}}_T^k$中为零的位置找出来，然后把${\mathbf{E}}_k$对应的位置删除，得到${\mathbf{E}}_k^{{}^{\prime }}$，此时优化问题可描述为:
  $$\underset{{\mathbf{d}}_k,{\mathbf{x}}_T^k}{\min }{\Vert {\mathbf{E}}_k^{{}^{\prime }}-{\mathbf{d}}_k{\mathbf{x}{}^{\prime }}_T^k\Vert }_F^2\text{\hspace{1em}(1-7)}$$
• 因此我们需要求出最优的 ${\mathbf{d}}_k,{{\mathbf{x}}^{{}^{\prime }}}_T^k$:
  $${\mathbf{E}}_k^{{}^{\prime }}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T\text{\hspace{1em}(1-8)}$$
• 取左奇异矩阵 $\mathbf{U}$ 的第1个列向量${\mathbf{u}}_1=U(\cdot ,1)$作为${\mathbf{d}}_k={\mathbf{u}}_1$，即${\mathbf{d}}_k$，取右奇异矩阵的第1个行向量与第1个奇异值的乘积作为${\mathbf{x}{}^{\prime }}_T^k$，即${\mathbf{x}{}^{\prime }}_T^k=\mathbf{\Sigma }(1,1){\mathbf{V}}^T(1,\cdot )$。得到${\mathbf{x}{}^{\prime }}_T^k$后，将其对应地更新到原${\mathbf{x}}_T^k$。
• 注意：式（1-8）所求得的奇异值矩阵 $\mathbf{\Sigma }$ 中的奇异值应从大到小排列；同样也有${\mathbf{x}{}^{\prime }}_T^k=\mathbf{\Sigma }(1,1)\mathbf{V}(\cdot ,1{)}^T$，这与上面x′kT的求法是相等的。

1.3、字典学习算法实现

利用1.2小节稀疏算法求解得到稀疏矩阵$\mathbf{X}$后，逐列更新字典，有如下算法1.1。

算法	字典学习（K-SVD）
输入	原始样本，字典，稀疏矩阵
输出	字典，稀疏矩阵
1 初始化	从原始样本$Y\in {\mathbf{R}}^{m\times n}$随机取$K$个列向量或者取它的左奇异矩阵的前$K$个列向量 { d 1 , d 2 , ⋯ , d K } \{\mathbf{d}_1,\mathbf{d}_2,\cdots,\mathbf{d}_K\} {d1​,d2​,⋯,dK​}作为初始字典的原子，得到字典${\mathbf{D}}^{(0)}\in {\mathbf{R}}^{m\times K}$。令$j=0$， 重复下面步骤1-3，直到达到指定的迭代步数，或收敛到指定的误差：
2 稀疏编码	利用字典上一步得到的字典${\mathbf{D}}^{(j)}$，稀疏编码，得到${\mathbf{X}}^{(j)}\in {\mathbf{R}}^{K\times n}$。
3 字典更新	逐列更新字典${\mathbf{D}}^{(j)}$，字典的列 d k ∈ { d 1 , d 2 , ⋯ , d K } \mathbf{d}_k \in \{\mathbf{d}_1,\mathbf{d}_2,\cdots,\mathbf{d}_K\} dk​∈{d1​,d2​,⋯,dK​}
3.1	当更新${\mathbf{d}}_k$时，计算误差矩阵${\mathbf{E}}_k$: ${\mathbf{E}}_k=\mathbf{Y}-{\sum }_{j\ne k}{\mathbf{d}}_j{\mathbf{x}}_T^j.$
3.2	取出稀疏矩阵第$k$个行向量${\mathbf{x}}_T^k$不为0的索引的集合${\omega }_k=\left\{i1\le i\le n,{\mathbf{x}}_T^k(i)\ne 0\right\}$ 还有以下的这个： x ′ T k = { x T k ( i ) 1 ≤ i ≤ n , x T k ( i ) ≠ 0 } \mathbf{x'}_T^{k} = \{\mathbf{x}_T^k(i)1\le i\le n,\ \mathbf{x}_T^k(i) \ne 0\} x′Tk​={xTk​(i)1≤i≤n, xTk​(i)​=0}
3.3	从${\mathbf{E}}_k$取出对应${\omega }_k$不为0的列，得到${\mathbf{E}}_k^{{}^{\prime }}$,
3.4	对${\mathbf{E}}_k^{{}^{\prime }}$作奇异值分解${\mathbf{E}}_k=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T;$取$U$的第1列更新字典的第$k$列，即 ${\mathbf{d}}_k=\mathbf{U}(\cdot ,1)$, 令：${{\mathbf{x}}^{\prime }}_T^k=\mathbf{\Sigma }(1,1)\mathbf{V}(\cdot ,1{)}^T$；得到${{\mathbf{x}}^{\prime }}_T^k$后，将其对应地更新到原${\mathbf{x}}_T^k$。
3.5	$j=j+1$

最后感谢作者：

• https://www.cnblogs.com/endlesscoding/p/10090866.html