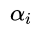语音增强--------------字典学习

字典学习就是用较少的特征（原子）来表示信号，那么信号的多个特征组合就相当于多个原子组成的字典，那么信号就可以用字典中少量的原子进行表示。信号在字典下的表示系数越系数，那么重构信号的质量就越高。常见的字典学习分为：固定字典学习和自适应字典学习，前者没有利用信号的有用信息，所以实际中一般使用的是自适应字典学习

稀疏表示

对于信号$\mathbf{x}\left(\mathbf{x}\in {\mathbb{R}}^{m\times 1}\right)$来说，其稀疏表示模型为
$$\mathbf{x}=\mathbf{D}\mathbf{c}+\mathbf{e}$$
其中$\mathbf{D}\in {\mathbb{R}}^{m\times n}$表示原子个数为$n$，每个原子包含有$m$个元素的字典，一般取冗余字典，即$n>m$。$\mathbf{c}\in {\mathbb{R}}^{n\times 1}$为稀疏表示系数，$\mathbf{e}\in {\mathbb{R}}^{m\times 1}$为稀疏表示误差，由于字典的冗余性，系数$\mathbf{c}$不唯一，一般要求解的是最稀疏的$\mathbf{c}$，求解的过程可以表示为
$${\mathbf{c}}^{\ast }=\arg \underset{\mathbf{c}}{\min }{\Vert \mathbf{x}-\mathbf{D}\mathbf{c}\Vert }_{2}s.t.f\left(\mathbf{c}\right)\le q$$
或者
$${\mathbf{c}}^{\ast }=\arg \underset{\mathbf{c}}{\min }f\left(\mathbf{c}\right)s.t.{\Vert \mathbf{x}-\mathbf{D}\mathbf{c}\Vert }_2\le \xi$$
其中，$q$是稀疏表示系数$\mathbf{c}$的稀疏度约束，$\xi$是设置的稀疏表示误差阈值，$f\left(\mathbf{c}\right)$是对向量$\mathbf{c}$的稀疏性度量函数，常用的有$l_0$和$l_1$范数。当使用$l_0$范数时，目标函数为非凸问题，相应的稀疏表示方法为MP算法和OMP算法。当使用$l_1$范数时， 常用的稀疏表示方法有BP算法和LARS算法。

OMP算法

由于求解$l_0$范数是NP-Hard的，所以经常采用贪婪追踪的方法来解决这类问题。OMP算法是在MP算法的基础上改进来的，由于MP算法在迭代的时候不能保证信号或者误差在已选择的原子上的投影是正交的，导致每步迭代并不是最优的，为了解决这个问题， OMP算法应运而生。在OMP算法过程中，每步迭代包括：原子选择和系数更新。具体过程为：

Input：$\mathbf{x}\in {\mathbb{R}}^{m\times 1}$；$\mathbf{D}\in {\mathbb{R}}^{m\times n}$, $q$ or $\xi$

Output：$\mathbf{c}\in {\mathbb{R}}^{n\times 1}$

Initialization：

$\mathbf{c}\leftarrow 0$；$\mathbf{e}\leftarrow \mathbf{x}$； ψ ← { } \psi \leftarrow \{\} ψ←{}

while $\Vert \mathbf{c}\Vert \le q$ and ${\Vert \mathbf{e}\Vert }_2\ge \xi$

         $\mu ={\mathbf{D}}^T\mathbf{e}$

         $j^{\ast }\leftarrow \arg \underset{j}{\max }\left|{\mu }_j\right|,j\in {\psi }^c$

          ψ ← ψ ∪ { j ∗ } \psi \leftarrow \psi \cup \left\{ {{j}^{*}} \right\} ψ←ψ∪{j∗}

         ${\mathbf{c}}_{\psi }=\arg \underset{\mathbf{c}}{\max }{\Vert \mathbf{x}-{\mathbf{D}}_{\psi }\mathbf{c}\Vert }_2,{\mathbf{c}}_{\psi }\leftarrow {\left({\mathbf{D}}_{\psi }^T{\mathbf{D}}_{\psi }\right)}^{-1}{\mathbf{D}}_{\psi }^T\mathbf{x}$

         $\mathbf{e}\leftarrow \mathbf{x}-\mathbf{D}\mathbf{c}$

end

LARC算法

为了降低$l_0$范数的求解难度，将$l_0$范数松弛到$l_1$范数。LARS算法是求解$l_1$范数稀疏表示的有效方法。同样地，该算法也包括了原子选择和系数更新两个步骤。原子选择部分与OMP算法基本相同，在系数更新方面，与OMP算法不同的是，该算法是沿着已选择的字典原子的角平分线上寻找新的字典原子，使得该字典原子与残差的相关性等同于已挑选原子与残差的相关性，再更新相应的步长，直到选择了所有的字典原子或者满足稀疏度或表示误差的要求时终止算法。
后来，有人提出了一种改进的方法，即LARC算法。其主要改进为：定义了Gram矩阵，即$\mathbf{G}={\mathbf{D}}^T\mathbf{D}$，并在每次迭代过程中采用Cholesky 分解更新该矩阵，避免了重复计算${\mathbf{D}}_{\psi }^T{\mathbf{D}}_{\psi }$，从而降低了计算量；提出了采用误差相关阈值$\mu$作为算法的终止条件，减少了不必要的迭代，避免了对观察信号幅值大小的依赖。具体过程为

Input：$\mathbf{x}\in {\mathbb{R}}^{m\times 1}$；$\mathbf{D}\in {\mathbb{R}}^{m\times n}$, $\mathbf{G}={\mathbf{D}}^T\mathbf{D}$, $\mu$。

Output：$\mathbf{c}\in {\mathbb{R}}^{n\times 1}$

Initialization：

$\mathbf{c}\leftarrow 0$；$\mathbf{y}\leftarrow 0$； ψ ← { } \psi \leftarrow \{\} ψ←{}

${\mu }^{\left(\mathbf{x}\right)}\leftarrow {\mathbf{D}}^T\mathbf{x}$；${\mu }^{\left(\mathbf{y}\right)}\leftarrow 0$

when $\left|\psi \right|<D$：

         $\mu \leftarrow {\mu }^{\left(\mathbf{x}\right)}-{\mu }^{\left(\mathbf{y}\right)}$

         $j^{\ast }\leftarrow \arg \underset{j}{\max }\left|{\mu }_j\right|,j\in {\psi }^c$

          ψ ← ψ ∪ { j ∗ } \psi \leftarrow \psi \cup \left\{ {{j}^{*}} \right\} ψ←ψ∪{j∗}

         if $\left|{\mu }_{j^{\ast }}\right|/{\Vert \mathbf{x}-\mathbf{y}\Vert }_2<\mu$

                       break

         end

         $\mathbf{s}\leftarrow sign\left({\mu }_{\psi }\right)$

         $\mathbf{g}\leftarrow {\mathbf{G}}_{\left(\psi ,\psi \right)}^{-1}\mathbf{s}$

         $b\leftarrow {\left({\mathbf{g}}^T\mathbf{s}\right)}^{-\frac{1}{2}}$

         $\mathbf{w}\leftarrow b\mathbf{g}$

         $\mathbf{u}\leftarrow {\mathbf{D}}_{\left(:,\psi \right)}\mathbf{w}$

         $\mathbf{a}\leftarrow {\mathbf{G}}_{\left(:,\psi \right)}\mathbf{w}$

         $\gamma \leftarrow {\min }_{k\in {\psi }^c}^{+}\left[\begin{array}{cc}\left(\left|{\mu }_{j^{\ast }}\right|-\left|{\mu }_k\right|\right)/\left(b-a_k\right),& \left(\left|{\mu }_{j^{\ast }}\right|+\left|{\mu }_k\right|\right)/\left(b+a_k\right)\end{array}\right]$

         $\mathbf{y}\leftarrow \mathbf{y}+\gamma \mathbf{u}$

         ${\mathbf{c}}_{\psi }\leftarrow {\mathbf{c}}_{\psi }+\gamma \mathbf{w}$

         ${\mu }^{\left(\mathbf{y}\right)}\leftarrow {\mu }^{\left(\mathbf{y}\right)}+\gamma \mathbf{a}$

end

自适应字典学习

字典学习的方法主要分两类：一类是通过预先设置的数学变换来构造字典的固定字典解析方法，包括离散余弦变换、小波变换等，但是该类方法没有利用到信号的特有信息，原子形态比较单一；一类是通过自适应的方式来获取字典，这样字典原子与信号之间有很好的相干性，使得其更加灵活。下面简单地介绍几种自适应字典学习的方法。

K-SVD算法

字典学习的目的就是为了将信号$\mathbf{X}\in {\mathbb{R}}^{m\times r}$近似地分解为字典$\mathbf{D}\in {\mathbb{R}}^{m\times n}$和稀疏表示系数矩阵$\mathbf{C}\in {\mathbb{R}}^{n\times r}$，相应的目标函数为
$$\arg \underset{\mathbf{D},\mathbf{C}}{\min }{\Vert \mathbf{X}-\mathbf{D}\cdot \mathbf{C}\Vert }_F^2$$
从上面可以看出，该优化目标中存在两个未知数，对于该非凸问题，有研究学者提出了交替更新$\mathbf{D}$和$\mathbf{C}$直至算法收敛到局部最优解。固定字典$\mathbf{D}$，求解稀疏表示系数$\mathbf{C}$的过程称为稀疏编码或者稀疏表示；固定稀疏表示系数$\mathbf{C}$，求解字典$\mathbf{D}$的过程称为字典学习。在K-SVD字典学习中，稀疏表示的方法使用的是OMP算法，字典更新的模型可以表示为
$$\begin{array}{rl}& \mathbf{D}\leftarrow \arg \underset{D}{\min }{\Vert \mathbf{X}-\mathbf{D}\cdot \mathbf{C}\Vert }_F^2\\ & s.t.{\Vert {\mathbf{d}}_{\left(:,l\right)}\Vert }_2=1\forall l=1,...,n\end{array}$$
K-SVD在更新字典时，对原子进行逐个更新，同时也有稀疏表示系数的更新。在更新原子时，
$$\begin{array}{rl}& {\Vert \mathbf{X}-\mathbf{D}\cdot \mathbf{C}\Vert }_F^2\text{=}{\Vert \mathbf{X}-\sum _{i=1}^n{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}\Vert }_F^2\\ & ={\Vert \left(\mathbf{X}-\sum _{i\ne l}{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}\right)-{\mathbf{d}}_{\left(:,l\right)}{\mathbf{c}}_{\left(l,:\right)}\Vert }_F^2\\ & ={\Vert {\mathbf{R}}^{\left(l\right)}-{\mathbf{d}}_{\left(:,l\right)}{\mathbf{c}}_{\left(l,:\right)}\Vert }_F^2\end{array}$$
它的主要思想就是将$\mathbf{D}\cdot \mathbf{C}$分解成$n$个秩一的矩阵，使得该稀疏表示误差项最小。在更新第$l$列的原子${\mathbf{d}}_{\left(:,l\right)}$时，可以假设第$l$个原子未知，固定其他$n-1$列原子，通过最小化上述表达式使得${\mathbf{d}}_{\left(:,l\right)}{\mathbf{c}}_{\left(l,\upsilon \right)}$不断逼近${\mathbf{R}}_{\left(:,\upsilon \right)}^{\left(l\right)}$来更新${\mathbf{d}}_{\left(:,l\right)}$，其中 υ = { j ∣ C l , j ≠ 0 , 1 ≤ j ≤ n } \upsilon =\left\{ j|{{C}_{l,j}}\ne 0,1\le j\le n \right\} υ={j∣Cl,j​​=0,1≤j≤n}。具体是对${\mathbf{R}}^{\left(l\right)}$进行SVD分解，将最大奇异值对应的左奇异列向量来更新${\mathbf{d}}_{\left(:,l\right)}$，将其对应的右奇异矩阵的列向量来更新${\mathbf{c}}_{\left(l,:\right)}$。由于SVD不能保证${\mathbf{c}}_{\left(l,:\right)}$是稀疏的，但是在SVD过程中仅在非零元空间$\upsilon$内进行，即得到的系数${\mathbf{c}}_{\left(l,\upsilon \right)}$仅仅会更新${\mathbf{c}}_{\left(l,:\right)}$中对应位置的非零元，最终仍能保证稀疏表示系数的稀疏性。
具体过程为：

Input：$\mathbf{X}\in {\mathbb{R}}^{m\times r}$；${\mathbf{D}}_0\in {\mathbb{R}}^{m\times n}$；$q$ or $\xi$；$J$

Output：$\mathbf{D}$，$\mathbf{C}$

while $j_s<J$:

         Sparse Coding: OMP Algorithm

         Dictionary Updating:

         for $l\leftarrow 1$ to $n$:

                  ${\mathbf{d}}_{\left(:,l\right)}\leftarrow 0$

                   υ = { j ∣ C l , j ≠ 0 , 1 ≤ j ≤ n } \upsilon =\left\{ j|{{C}_{l,j}}\ne 0,1\le j\le n \right\} υ={j∣Cl,j​​=0,1≤j≤n}

                  ${\mathbf{R}}^{\left(l\right)}\leftarrow \mathbf{X}-\sum _{i\ne l}{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}$

                  ${\mathbf{R}}_{\left(:,\upsilon \right)}^{\left(l\right)}=\mathbf{U}\sum {\mathbf{V}}^T$

                  ${\mathbf{d}}_{\left(:,l\right)}\leftarrow {\mathbf{U}}_{\left(:,1\right)}$

                  ${\mathbf{c}}_{\left(l,\upsilon \right)}\leftarrow \sum \left(1,1\right){\mathbf{V}}_{\left(:,1\right)}$

         end

$j_s\leftarrow j_s+1$

end

近似K-SVD

由于每次迭代都需要进行SVD，增加了计算的复杂度，为了进一步降低K-SVD算法的复杂度，有学者提出了采用批量正交匹配追踪方法替代SVD 分解来近似完成K-SVD 算法，即
$${\mathbf{d}}_{\left(:,l\right)}\leftarrow {\mathbf{X}\mathbf{c}}_{{}_{\left(l,:\right)}}^T-\left(\sum _{i\ne l}{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}\right){\mathbf{c}}_{{}_{\left(l,:\right)}}^T$$
$${\mathbf{d}}_{\left(:,l\right)}\leftarrow {{\mathbf{d}}_{\left(:,l\right)}/\Vert {\mathbf{d}}_{\left(:,l\right)}\Vert }_2$$
$${\mathbf{c}}_{\left(l,:\right)}\leftarrow {\mathbf{X}}^T{\mathbf{d}}_{\left(:,l\right)}-{\left(\sum _{i\ne l}{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}\right)}^T{\mathbf{d}}_{\left(:,l\right)}$$
从上面可以看出迭代的过程不需要计算${\mathbf{R}}^{\left(l\right)}$，将原有的矩阵运算变成了向量的操作，并且不需要进行SVD。具体过程为：

Input：$\mathbf{X}\in {\mathbb{R}}^{m\times r}$；${\mathbf{D}}_0\in {\mathbb{R}}^{m\times n}$；$q$ or $\xi$；$J$

Output：$\mathbf{D}$，$\mathbf{C}$

while $j_s<J$:

         Sparse Coding: OMP Algorithm

         Dictionary Updating:

         for $l\leftarrow 1$ to $n$:

                  ${\mathbf{d}}_{\left(:,l\right)}\leftarrow 0$

                   υ = { j ∣ C l , j ≠ 0 , 1 ≤ j ≤ n } \upsilon =\left\{ j|{{C}_{l,j}}\ne 0,1\le j\le n \right\} υ={j∣Cl,j​​=0,1≤j≤n}

                  ${\mathbf{d}}_{\left(:,l\right)}\leftarrow {\mathbf{X}\mathbf{c}}_{{}_{\left(l,:\right)}}^T-\left(\sum _{i\ne l}{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}\right){\mathbf{c}}_{{}_{\left(l,:\right)}}^T$

                  ${\mathbf{d}}_{\left(:,l\right)}\leftarrow {{\mathbf{d}}_{\left(:,l\right)}/\Vert {\mathbf{d}}_{\left(:,l\right)}\Vert }_2$

                  ${\mathbf{c}}_{\left(l,:\right)}\leftarrow {\mathbf{X}}^T{\mathbf{d}}_{\left(:,l\right)}-{\left(\sum _{i\ne l}{\mathbf{d}}_{\left(:,i\right)}{\mathbf{c}}_{\left(i,:\right)}\right)}^T{\mathbf{d}}_{\left(:,l\right)}$

         end

$j_s\leftarrow j_s+1$

end

NMF算法

NMF是在所有矩阵元素非负的约束下的分解方式，在语音信号中对应其幅度谱或者功率谱，如
$$\mathbf{X}=\mathbf{D}\mathbf{C}$$
$\mathbf{X}\in {\mathbb{R}}_{+}^{n\times m}$为待分解矩阵，$\mathbf{D}\in {\mathbb{R}}_{+}^{n\times r}$（基矩阵）和$\mathbf{C}\in {\mathbb{R}}_{+}^{r\times m}$（系数矩阵）为分解后的两个矩阵。一般用距离来衡量两者的相似程度，可以进一步将优化目标写作为
$$\underset{\mathbf{D},\mathbf{C}}{\min }{D}_{\alpha }\left(\mathbf{X}|\mathbf{D}\mathbf{C}\right)$$
其中$D_{\alpha }\left(\cdot \right)$表示$\mathbf{X}$和$\mathbf{D}\mathbf{C}$之间的距离
D α ( x ∣ y ) = { 1 α ( α − 1 ) ( x α − y α − α x y α − 1 ( x − y ) ) , α ∈ R \ { 0 , 1 } x ( log ⁡ x − log ⁡ y ) + ( y − x ) , α = 1 x y − log ⁡ x y − 1 , α = 0 {{D}_{\alpha }}\left( x|y \right)\text{=}\left\{ \begin{aligned} & \frac{1}{\alpha }\left( \alpha -1 \right)\left( {{x}^{\alpha }}-{{y}^{\alpha }}-\alpha x{{y}^{\alpha -1}}\left( x-y \right) \right),\ \ \ \ \ \ \ \alpha \in \mathbb{R}\backslash \left\{ 0,1 \right\} \\ & x\left( \log x-\log y \right)+\left( y-x \right),\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \alpha =1 \\ & \frac{x}{y}-\log \frac{x}{y}-1,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \alpha =0 \\ \end{aligned} \right. Dα​(x∣y)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​​α1​(α−1)(xα−yα−αxyα−1(x−y)),       α∈R\{0,1}x(logx−logy)+(y−x),                      α=1yx​−logyx​−1,                                       α=0​
当$\alpha =0$时，对应的是Itakura-Saito距离；当$\alpha =1$时，对应的是广义KL散度；当$\alpha =2$时，对应的是欧氏距离。一般来说，后两者较为常见。
对于NMF算法的基矩阵和系数矩阵，利用梯度下降可以得到相应的更新过程
$$\mathbf{C}\leftarrow \mathbf{C}\otimes \frac{\mathbf{D}\left[{\left(\mathbf{D}\mathbf{C}\right)}^{\alpha -2}\otimes \mathbf{X}\right]}{{\mathbf{D}}^T{\left(\mathbf{D}\mathbf{C}\right)}^{\alpha -1}}$$
$$\mathbf{D}\leftarrow \mathbf{D}\otimes \frac{\left[{\left(\mathbf{D}\mathbf{C}\right)}^{\alpha -2}\otimes \mathbf{X}\right]{\mathbf{C}}^T}{{\left(\mathbf{D}\mathbf{C}\right)}^{\alpha -1}{\mathbf{C}}^T}$$
上式中的所有运算均为元素之间的运算。
同样地，上式更新过程并没有对系数矩阵进行稀疏度的约束，如果增加稀疏度约束，那么相应的目标函数变为
$$\underset{\mathbf{D},\mathbf{C}}{\min }{D}_{\alpha }\left(\mathbf{X}|\mathbf{D}\mathbf{C}\right)\text{+}\mu {\Vert \mathbf{C}\Vert }_1$$
相应地，对于系数矩阵的更新则变为
$$\mathbf{C}\leftarrow \mathbf{C}\otimes \frac{\mathbf{D}\left[{\left(\mathbf{D}\mathbf{C}\right)}^{\alpha -2}\otimes \mathbf{X}\right]}{{\mathbf{D}}^T{\left(\mathbf{D}\mathbf{C}\right)}^{\alpha -1}\text{+}\mu }$$
对于单通道语音增强来说，NMF算法是比较简单有效的，但是也存在着一些缺点，比如线性假设，乘法更新的复杂度等等。
选用NMF算法进行语音增强，仿真参数设置如下。

仿真参数设置

参数名称	参数值
信噪比	10dB
采样率	8KHz
SFFT点数	512
字典原子个数	100

实验结果如下：

可以看出经过NMF算法处理后的带噪语音有了明显的改善效果，这也说明了该方法的有效性。

关于语音及噪声文件，具体请参考：语音信号处理常用语料库下载地址

参考文献：
[1]罗友. 基于联合字典学习和稀疏表示的语音降噪算法研究[D].中国科学技术大学,2016.
[2]朱媛媛. 基于稀疏表示和深度学习的有监督语音增强算法研究[D].中国科学技术大学,2020.