描述

n个人围成一圈（编号为1 - n），从第1个人开始报数，报到k的人出列，后面的人重新从1开始报数。问最后剩下的人的编号。

例如：n = 3，k = 2。2号先出列，然后是1号，最后剩下的是3号。

输入
输入为单组测试数据。

输入2个数n和k，表示n个人，数到k出列。(2 <= n, k <= 200)

输出
输出一个整数表示最后剩下的人的编号。

输入样例 1

10 3

输出样例 1

4

此题为经典的约瑟夫环问题，下面简单地了解一下这个问题：

一、问题的来历
据说著名犹太历史学家 Josephus有过以下的故事：在罗马人占领乔塔帕特后，39个犹太人与Josephus及他的朋友躲在一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。问题是，给定了总人数n和报数值m，一开始要站在什么地方才能避免被处决？Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

二、问题的基本描述
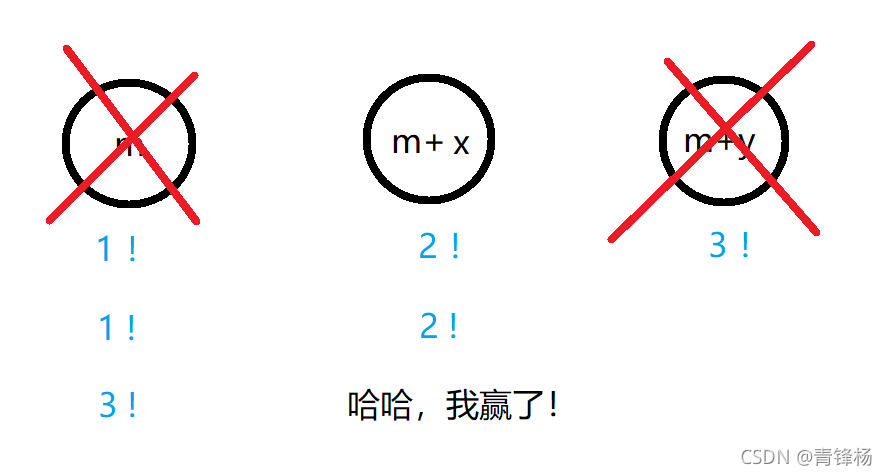
n个人围成圈，依次编号为1、2、3、…、n,从1号开始依次报数，报到m时，报m的人退出，下一个人重新从1报起，当报到m时，报m的人退出，如此循环下去，问最后剩下的那个人的编号是多少？

三、解题方法
（一）、队列

#include <iostream>
#include <queue>
using namespace std;
int main()
{int n, m;cin >> n >> m;queue<int> q;for (int i = 1; i <= n; i++){q.push(i);}int cur=1;while(q.size() > 1){int x = q.front();q.pop();if (cur == m){cur = 1;}else{q.push(x);cur++;}}cout << q.front() << endl;return 0;
}

（二）、指针

#include <stdio.h>int main()
{int i,k,t,m,n,num[50],*p;scanf("%d%d",&n,&m);p=num;for (i=0;i<n;i++)*(p+i)=i+1;i=0;k=0;t=0;while (t<n-1){if (*(p+i)!=0)k++;if (k==m){*(p+i)=0;k=0;t++;}i++;if (i==n)i=0;}while(*p==0)p++;printf("The last one is NO.%d\n",*p);return 0;
}

（三）、数组

#include<iostream>using namespace std;
int main()
{int n = 0;cin>>n;int arr[100];//初始数组for(int i = 0; i < n; i++)arr[i] = i+1;int count = 0;//报数计数int m = 0;//退出人数计数for(int i = 0; i<n; i++){if(arr[i]!=0){count++;if(m == n - 1){cout<<arr[i]<<endl;break;}if(count == 3){count = 0;m++;arr[i] = 0;}if(i == n - 1){i = -1;}}}return 0;
}

（四）、链表

#include<iostream>using namespace std;
struct number
{int num;struct number *next;
};
int main()
{int i,n,m;while(cin>>n>>m){struct number *p,per[100],*pre;for(i=0;i<n;i++){per[i].num=i+1; //初始化数值if(i==n-1)per[i].next=&per[0]; // <循环>链表的建立elseper[i].next=&per[i+1];}p=per;for(i=1;;i++){if(i==m){pre->next=p->next;cout<<p->num<<endl; // 数到m ,m退出,输出数值}if(i==m+1)i=1; //循环pre=p;p=p->next;if(p==pre)break; //只剩下最后一个了}cout<<p->num<<endl;}return 0;
}

（五）、公式法

#include <stdio.h>
int main()
{int n, m, i, s = 0;scanf("%d%d", &n, &m);for (i = 2; i <= n; i++){s = (s + m) % i;}printf ("%d\n", s+1);return 0;
}

以下是对约瑟夫环问题的补充,里面有关于公式法的详细讲解：

原文链接：https://blog.csdn.net/u011500062/article/details/72855826

PS：如果觉得我的文章对你有帮助或者有所启发的话，点赞鼓励一下吧！
如果我的文章有错，还望不吝赐教，嘻嘻！