B树的定义
flyfish 2015-7-15

B-树即为B树。因为B树的原英文名称为B-tree，因为翻译的不统一所以B树和B-树都是B-tree。

B树定义 引用自严蔚敏《数据结构》（C语言版）
B树是一种平衡的多路查找树
定义：一棵m 阶的B树，或者为空树，或为满足下列特性的m 叉树：
1 树中每个结点至多有m 棵子树；
2 若根结点不是叶子结点，则至少有两棵子树；
3 除根结点之外的所有非终端结点至少有$\left \lceil m/2 \right \rceil$棵子树；
4 所有的非终端结点中包含以下信息数据：
（n，$A_0$，$K_1$，$A_1$，$K_2$，$A_2$，…，$K_n$，$A_n$）
其中：$K_i$（i=1,…,n）为关键字，且$K_i$<$K_i$$_+$$_1$
$A_i$ (i=0，…，n)为指向子树根结点的指针，且指针$A_i$$_-$$_1$ 所指子树中所有结点的关键字均小于$K_i$ (i=1,…,n)，
$A_n$ 所指子树中所有结点的关键字均大于$K_n$.
n( $\left \lceil m/2 \right \rceil-1$$\leqslant n$$\leqslant m-1$)为关键字的个数(或者n+1为子树的个数)。
5 所有的叶子结点都出现在同一层次上，并且不带信息（可以看作是外部结点或查找失败的结点，实际上这些结点不存在，指向这些结点的指针为空）。

结点最大的孩子数目称为B树的阶(order)。

B树定义 引用自 Donald Knuth的《The Art of Computer programming》

A B-tree of order m is a tree that satisfies the following properties:
1 Every node has at most m children.
2 Every node, except for the root and the leaves, has at least m/2 children,
3 The root has at least 2 children (unless it is a leaf),
4 All leaves appear on the same level, and carry no information.
5 A nonleaf node with k children contains k - 1 keys.
翻译
1 树中每个结点至多有m个孩子；
2 除根结点和叶子结点外，其它每个结点至少有m/2个孩子；
3 若根结点不是叶子结点，则至少有2个孩子；
4 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息；
5 有k个孩子的非终端结点包含k-1个关键字。

向下取整floor，用数学符号$\left \lfloor \right \rfloor$表示
向上取整ceil，用数学符号$\left \lceil \right \rceil$表示
floor(7.5) = 7
floor(-7.5) = -8
ceil(7.5) = 8
ceil(-7.5) = -7

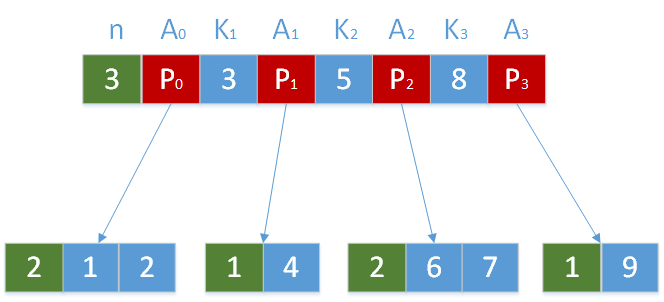
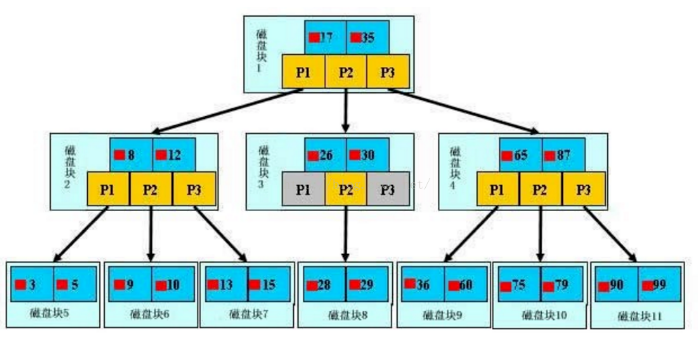
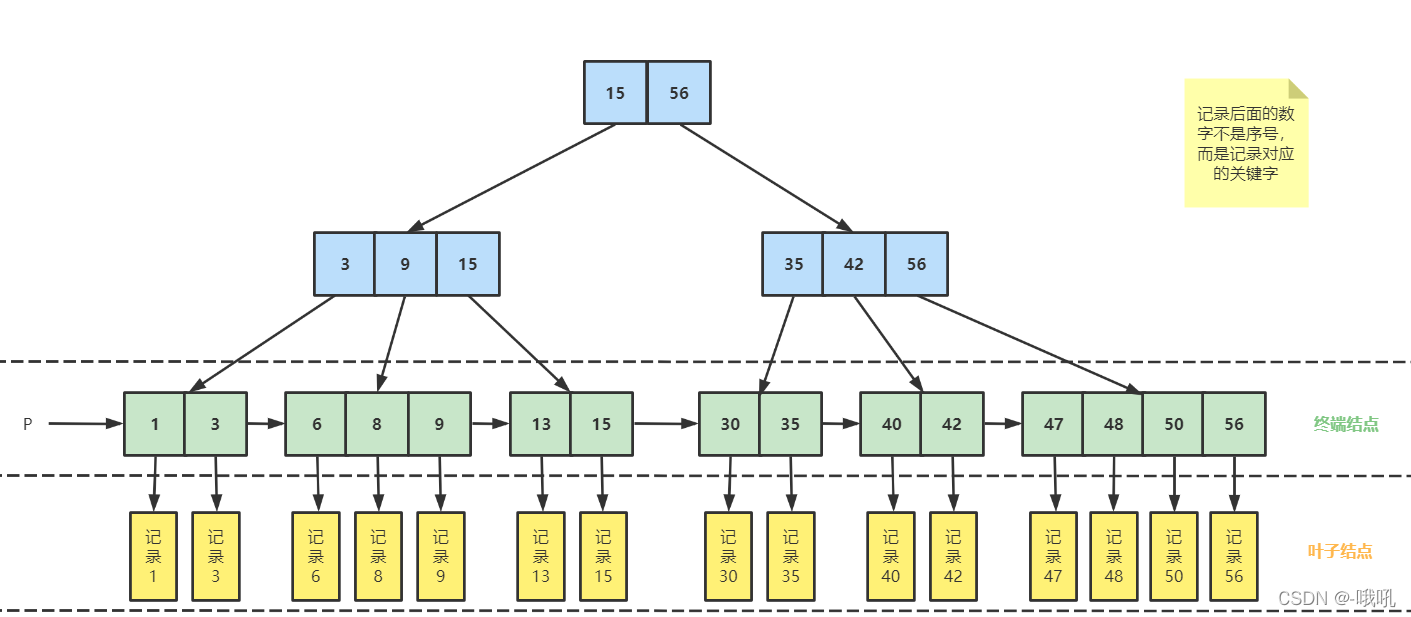
B树示意图
绿色：关键字个数
红色：指针
蓝色：关键字
关键字从1到9的B树

问题：
对于n个关键字的m阶B树，最坏情况需要查找几次？

同样的问题不同的问法
含n个关键字的m阶B树的最大深度是多少？

深度为h+1的m阶B树所具有的最少结点数是
第一层至少1个节点
第二层至少2个节点

除根节点外每个分支节点至少有m/2棵子树
所以层数与每层至少结点数的关系如下
1 = 1
2 = 2
3 = 2$\times$ $\left \lceil m/2 \right \rceil$
4 = 2$\times$( $\left \lceil m/2 \right \rceil$)$^{2}$
5 = 2$\times$( $\left \lceil m/2 \right \rceil$)$^{3}$
6 = 2$\times$( $\left \lceil m/2 \right \rceil$)$^{4}$
7 = 2$\times$( $\left \lceil m/2 \right \rceil$)$^{5}$
…
h = 2$\times$( $\left \lceil m/2 \right \rceil$)$^{h-2}$
h+1 = 2$\times$( $\left \lceil m/2 \right \rceil$)$^{h-1}$

h+1层的节点就是叶子节点。若m阶B树有n个关键字，则叶子节点即查找不成功的节点为n+1

推导
n+1 $\geqslant 2\times ( \left \lceil m/2 \right \rceil )^{h-1}$

2$\times$( $\left \lceil m/2 \right \rceil$)$^{h-1}$ $\leqslant$ n+1

( $\left \lceil m/2 \right \rceil$)$^{h-1}$$\leqslant$$\frac{n+1}{2}$

h-1$\leqslant$$\log_{ \left \lceil m/2 \right \rceil} (\frac{n+1}{2})$

h$\leqslant$$\log_{ \left \lceil m/2 \right \rceil} (\frac{n+1}{2})$+1

所以 含n个关键字的m阶B树的最大深度是
$\log_{ \left \lceil m/2 \right \rceil} (\frac{n+1}{2})$+1

读作 以${ \left \lceil m/2 \right \rceil}$为底 $(\frac{n+1}{2})$的对数 加1

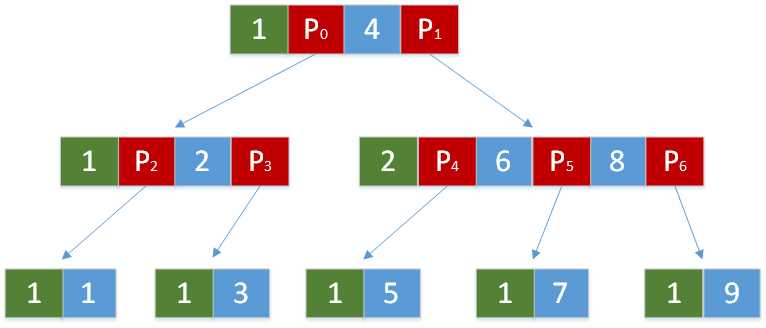
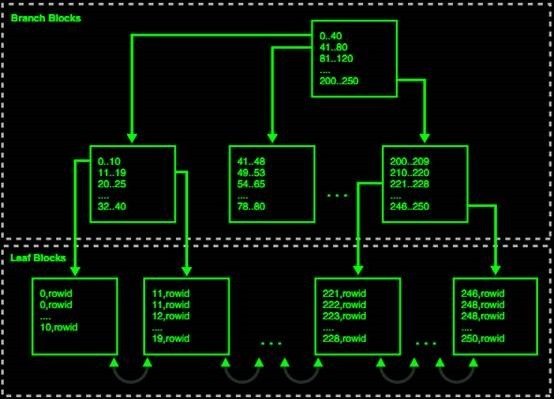
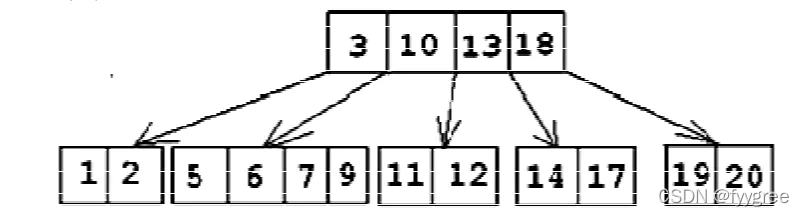
Degree为3,关键码从1到9的B树示意图
绿色：关键字个数
红色：指针
蓝色：关键字