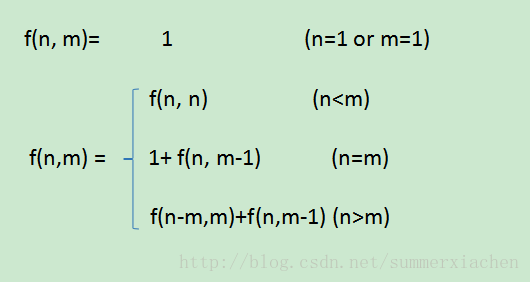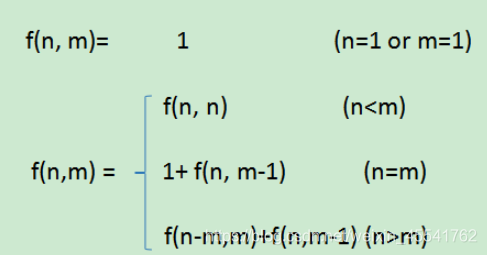题目大意:给定一个整数n,找到k个数,使得其和等于n。
如:
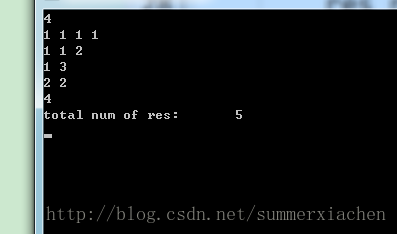
4=1+1+1+1
4=1+1+2;
4=1+3;
4=2+2;
4=4;求其分解的所有可能,并输出分解表达式。
解题思路:要拆分整数n,肯定先要找到一个元素,然后我们会发现,剩下的问题还是一个整数差分问题,因此容易得到问题的解。
定义函数f(n)为n可以拆分的解的个数,即可以先拆分出一个数字k(k = 1,2,……,n),然后再拆分f(k),可以得出有:
n=1+f(n-1);
n=2+f(n-2);
·····
n=(n-1)+f(1);
n=n+f(0)即
数学公式推导:
②-①
于是可以解得
在来想一想该用怎样的数据结构来存储描述,用数组,int res[max]用来暂存拆分元素。先拿简单的拆分来说事,拆分成两个数的情况。
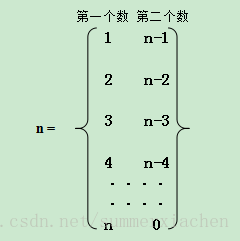
如何输出这拆分的表达式,看一眼就很明,循环1~n,输出即可。
//只拆分为两个数的时候
void resolve(int n)
{ //res用来暂存拆分元素//p是游标,初始值为p=0;for(int i=1;i<=n;i++){res[p]=i;p++;//下一个位置存储n-i;res[p]=n-i;//输出处理p--;//回归到起点。}
}分析上面的代码,再来看递推,如果分成三个数,那么在即将执行res[p]=n-i时,需要将n-i在一次分解成两个数,即resolve(n-i),这样就形成了递归。
那么递归的出口条件是什么呢,当需要分解的数是0时,已经不能在继续往下分了,所以递归出口就是
if(n<=0), 当进入递归出口的时候,表明本次已经分解完成,可以输出res中的数据。
整理上诉得到递归处理函数代码如下
void resolve(int n)
{ if(n<=0){ for (int i=0; i<p_res; i++) //输出 cout << res[i] << " "; cout << endl; return ;}for(int i=1;i<=n;i++){res[p]=i;p++;resolve(n-i);p--;}
}贴上可运行代码
#include <iostream>
using namespace std;
#define MAX 20
int res_num;
// 拆分元素暂存在res数组中
int res[MAX];
int p = 0;
// 将n进行拆分
void resolve(int n); int main() { while (1) { int n; cin >> n; resolve(n); cout << "total num of res:\t" << res_num << endl; res_num = 0; } return 0;
} void resolve(int n) { if (n<=0) { // 出口 for (int i=0; i<p; i++) cout << res[i] << " "; cout << endl; res_num++; } for (int i=1; i<=n; i++) { res[p] = i; p++; // p ++来顺序存储各个拆分元素 resolve(n-i); p--; // 此行必须有,执行完这一行,下一次for循环才能回退 }
} 测试结果如下:
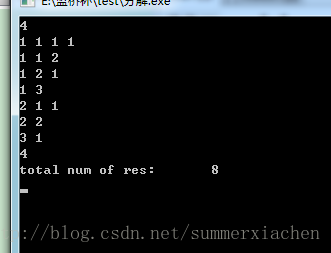
可以发现上述代码输出的结果有重复答案,如当n=4时,会输出1 3,和3 1两组解,其实他们是相同的。
如果要求答案不能重复呢?
同样,我们可以定义一个函数f(n, min_factor),其中min_factor表示n拆分后元素中的最小值,这样即可通过min_factor来限制for循环的初始值,达到拆分元素从小到大输出的目的,从而避免相同的解重复输出
稍微修改上述代码,即可得到解。
贴出完整可运行代码如下:
#include <iostream>
using namespace std;
#define MAX 20
int res_num;
// 拆分元素暂存在res数组中
int res[MAX];
int p = 0; // 将n进行拆分
void resolve(int n, int min_factor=1); int main() { while (1) { int n; cin >> n; resolve(n,1); cout << "total num of res:\t" << res_num << endl; res_num = 0; } return 0;
} void resolve(int n, int min_factor) { if (n<=0) { // 出口 for (int i=0; i<p; i++) cout << res[i] << " "; cout << endl; res_num++; } for (int i=min_factor; i<=n; i++) { // 此处修改 res[p] = i; p++; // p ++来顺序存储各个拆分元素 resolve(n-i, i);// 此处修改 p--; // // 此行必须有,执行完这一行,下一次for循环才能回退 }
} 附加类似练习
将一个数n的分解为因子的乘积形式,输出所有可能,并输出表达式。
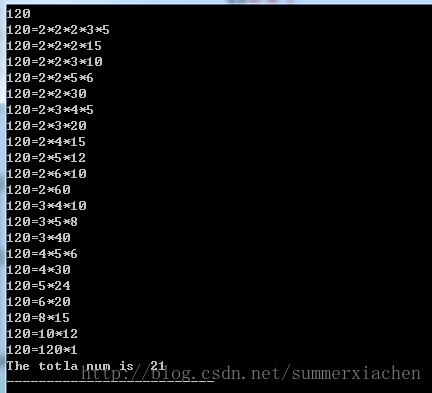
12=2*2*3;
12=2*6;
12=3*4;
12=6*2;
12=12*1;
解法与上述大同小异,不在累述。
代码如下
#include<iostream>
using namespace std;
int data[100];
int p=0;
int num=0;
int x;
void resolve(int n,int min)
{if(n<2) {num++;cout<<x<<"=";for(int j=0;j<p;j++){cout<<data[j];if(j!=p-1)cout<<"*";if(data[j]==x)cout<<"*1";}cout<<endl;return ;}for(int i=min;i<=n;i++){if(n%i==0){data[p]=i;p++; resolve(n/i,i);p--; }}
}
int main()
{while(cin>>x){resolve(x,2);cout<<"The totla num is "<<num<<endl;cout<<"--------------------------"<<endl;}
}【动态规划求解分解整数的总的可能情况数】
1、问题描述和分析
对于一个正整数n的分化,就是把n表示成一系列正整数之和的表达式。注意,分划与顺序无关,例如6=1+5 和 6=5+1被认为是同一个划分。另外,这个整数n本身也算是一种分化。
分析:
所谓整数划分,是指把一个正整数n写成如下形式: n=m1+m2+…+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,…,mi}为n的一个划分。
如果{m1,m2,…,mi}中的最大值不超过m,即max(m1,m2,…,mi)<=m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);
例如但n=4时,他有5个划分,{4},{3,1},{2,2},{2,1,1},{1,1,1,1};
2、数据结构和算法
该问题是求出n的所有划分个数,即f(n, m)。下面我们考虑求f(n,m)的方法,采用递归法, 根据n和m的关系,考虑以下几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
(2)当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,…,1};
(3)当n=m时,根据划分中是否包含n,可以分为两种情况:
(a)划分中包含n的情况,只有一个即{n};
(b)划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。
因此 f(n,n) =1 + f(n,n-1);
(4)当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5)但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(a)划分中包含m的情况,即{m, {x1,x2,…xi}}, 其中{x1,x2,… xi} 的和为n-m,因此这情况下为f(n-m,m);
(b)划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);
因此 f(n, m) = f(n-m, m)+f(n,m-1);
综上所述:
#include<stdio.h>
int Divintege(int n,int m)
{
if(n==1||m==1)return 1;
else if(n<m)return Divintege(n,n);
else if(n==m)return 1+Divintege(n,n-1);
elsereturn Divintege(n,m-1)+Divintege(n-m,m);
}int main(void)
{int n;while(scanf("%d",&n)!=EOF&&(n>=1)){printf("%d\n",Divintege(n,n));}return 0;
}