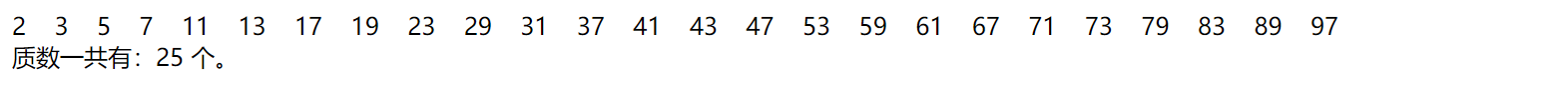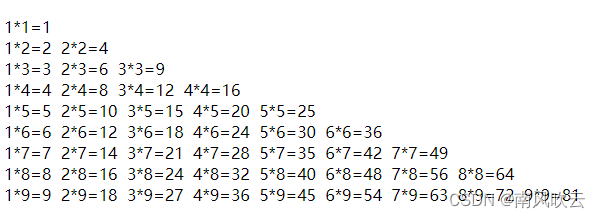史上最全的整数分解方法（包含经典的分苹果问题）

article/2025/11/11 1:46:51

【华为OD机试真题 2022&2023】真题目录 @点这里@

【华为OD机试真题】信号发射和接收 &试读& @点这里@

【华为OD机试真题】租车骑绿道 &试读& @点这里@

整数分解方法总结

一、加法分解：

题目描述：

给定一个正整数，我们可以定义出下面的公式：

N=a[1]+a[2]+a[3]+...+a[m];
a[i]>0,1<=m<=N;

对于一个正整数，求解满足上面公式的所有算式组合
对于整数4：

4 = 4；
4 = 3+1；
4 = 2+2；
4 = 2+1+1；
4 = 1+1+1+1；

1.所有可能的分解输出（有重复）

方法一：

#include <iostream>
using namespace std;
const int Size = 20;
int res_num;
// 拆分元素暂存在res数组中
int res[Size];
int a, p = 0;
// 将n进行拆分
void resolve(int n);int main() {while (1) {cin >> a;resolve(a);cout << "total num of res: " << res_num << endl;res_num = 0;}return 0;
}void resolve(int n) {if (n<=0) { // 出口cout << a << "=";for (int i=0; i<p-1; i++)cout << res[i] << "+";cout << res[p-1] << endl;res_num++;}for (int i = 1; i <= n; i++) {res[p] = i;p++;        // p ++来顺序存储各个拆分元素resolve(n-i);p--;        // 此行必须有，执行完这一行，下一次for循环才能回退}
}

方法二：

#include <iostream>
#include <vector>using namespace std;
int counts;
void Backtrack(int n, vector<int>& comb, int cur, int sum)
{int tmpSum;for (int num = 1; num <= n; num++){comb[cur] = num;tmpSum = sum + num;if (tmpSum > n){break;//最好换成break(原来为continue),因为当tmpSum>n之后继续循环是没有意义的}else if(tmpSum == n)//第一次输出前不断地递归，进入到最里面一层，当tmpSum==n时，通过for循环//输出全1的拆分结果，随后看是一层一层退出，依次分别执行外部的for循环，使得通过num的增加，而使//拆分的最后一位数字增加（中间可能涉及前进和后退的过程，通过tmpSum<n前进，tmpSum>n回退，回退//之后num在原数值基础上继续增加，导致拆分的最后一位数字增加）回退到最外面一层for循环之后，num//增加使得输出拆分结果的第一个数字增加。{cout << n << "=";for (int i = 1; i < cur; i++)cout << comb[i] << "+";cout << comb[cur] << endl;counts++;}else{Backtrack(n, comb, cur + 1, tmpSum);}}
}
int main()
{int n;vector<int> com;while (cin >> n){com.assign(n+1, 1);Backtrack(n, com, 1, 0);cout << "The total number is: " << counts << endl;}return 0;
}
结果如下：

在这里插入图片描述

2.输出不重复的分解结果

方法一改：

#include <iostream>
using namespace std;
const int Size = 20;
int res_num;
// 拆分元素暂存在res数组中
int res[Size];
int a, p = 0;
// 将n进行拆分
void resolve(int n, int flag);int main() {while (1) {cin >> a;resolve(a, 1);cout << "total num of res: " << res_num << endl;res_num = 0;}return 0;
}void resolve(int n, int flag) {if (n<=0) { // 出口cout << a << "=";for (int i=0; i<p-1; i++)cout << res[i] << "+";cout << res[p-1] << endl;res_num++;}for (int i = flag; i <= n; i++) {res[p] = i;p++;        // p ++来顺序存储各个拆分元素resolve(n-i, i);p--;        // 此行必须有，执行完这一行，下一次for循环才能回退}
}

方法二改：

#include <iostream>
#include <vector>using namespace std;
void Backtrack(int n, vector<int>& comb, int cur, int sum)
{int tmpSum;for (int num = comb[cur-1]; num <= n; num++){comb[cur] = num;tmpSum = sum + num;if (tmpSum > n){break;//最好换成break(原来为continue),因为当tmpSum>n之后继续循环是没有意义的}else if(tmpSum == n)//第一次输出前不断地递归，进入到最里面一层，当tmpSum==n时，通过for循环//输出全1的拆分结果，随后看是一层一层退出，依次分别执行外部的for循环，使得通过num的增加，而使//拆分的最后一位数字增加（中间可能涉及前进和后退的过程，通过tmpSum<n前进，tmpSum>n回退，回退//之后num在原数值基础上继续增加，导致拆分的最后一位数字增加）回退到最外面一层for循环之后，num//增加使得输出拆分结果的第一个数字增加，而由for循环的初始条件num=comb[cur-1]及comb[cur]=num，//决定了每次输出的拆分结果，后面的数字不小于前一位数字。{cout << n << "=";for (int i = 1; i < cur; i++)cout << comb[i] << "+";cout << comb[cur] << endl;}else{Backtrack(n, comb, cur + 1, tmpSum);}}
}
int main()
{int n;vector<int> com;while (cin >> n){com.assign(n+1, 1);Backtrack(n, com, 1, 0);}return 0;
}
输出结果：

在这里插入图片描述

二、触类旁通之乘法分解：

将一个数n的分解为因子的乘积形式，输出所有可能，并输出表达式。

12=2*2*3；
12=2*6；
12=3*4；
12=6*2；
12=12*1；
代码如下：
#include<iostream>
using namespace std;int data_s[100]; // 存储因子的数组
int p=0; // 因子数组的指针
int num=0; // 记录分解因子的总数
int x; // 待分解的数// 递归函数，用于分解因子
void resolve(int n,int minNum)
{if(n<2) // 如果n小于2，说明已经分解完毕{num++; // 记录分解因子的总数cout<< x << "="; // 输出待分解的数for(int j=0;j<p;j++){cout<< data_s[j]; // 输出因子if(j!=p-1)cout << "*"; // 输出乘号if(data_s[j] == x)cout << "*1"; // 如果因子等于待分解的数，输出*1}cout << endl; // 换行return;}for(int i=minNum;i<=n;i++) // 从minNum开始枚举因子{if(n%i==0) // 如果n能够整除i，说明i是n的因子{data_s[p]=i; // 将i存储到因子数组中p++; // 指针后移resolve(n/i, i); // 递归分解n/i的因子，最小因子为ip--; // 回溯，指针前移}}
}int main()
{while(cin >> x) // 循环读入待分解的数{resolve(x, 2); // 分解因子cout<< "The total numbers is  " << num << endl; // 输出分解因子的总数cout << "--------------------------" << endl; // 输出分隔符num = 0; // 重置分解因子的总数break;}return 0;}

在这里插入图片描述

下面的代码可以实现从小到大的顺序输出质数因子的乘积：

#include <iostream>
const int Num = 100;
using namespace std;int main()
{int data[Num],n; // 定义一个数组data和一个整数nwhile (cin >> n) // 循环读入n的值{int num = n,j = 0; // 定义一个整数num和一个计数器jfor (int i = 2; i <= n; ++i) // 从2到n遍历每个数{while (num % i == 0) // 如果num能被i整除{num /= i; // 将num除以idata[j] = i; // 将i存入数组data中j++; // 计数器加1}}for (int i = 0; i < j; ++i) // 遍历数组data{cout << data[i]; // 输出数组元素if (i != j - 1)cout << '*'; // 如果不是最后一个元素，输出乘号}cout << '=' << n << endl; // 输出等号和n的值}return 0;
}

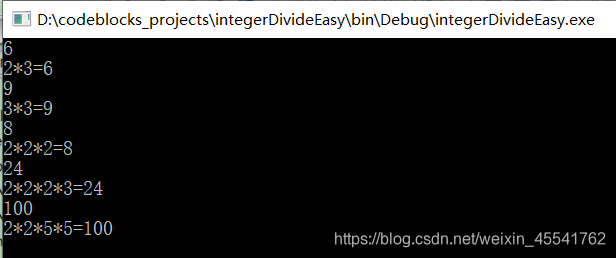
在这里插入图片描述

如果需要输出所有分解组合，只需要将resolve()的第二个参数去掉即可，如下面这段代码，输出所有因子组合（有重复）：

#include<iostream>
using namespace std;int data_s[100]; // 存储因子的数组
int p=0; // 因子数组的指针
int num=0; // 记录分解因子的总数
int x; // 待分解的数// 递归函数，用于分解因子
void resolve(int n)
{if(n<2) // 如果n小于2，说明已经分解完毕{num++; // 记录分解因子的总数cout<< x << "="; // 输出待分解的数for(int j=0;j<p;j++){cout<< data_s[j]; // 输出因子if(j!=p-1)cout << "*"; // 输出乘号if(data_s[j] == x)cout << "*1"; // 如果因子等于待分解的数，输出*1}cout << endl; // 换行return;}for(int i=2;i<=n;i++) // 从minNum开始枚举因子{if(n%i==0) // 如果n能够整除i，说明i是n的因子{data_s[p]=i; // 将i存储到因子数组中p++; // 指针后移resolve(n/i); // 递归分解n/i的因子，最小因子为ip--; // 回溯，指针前移}}
}int main()
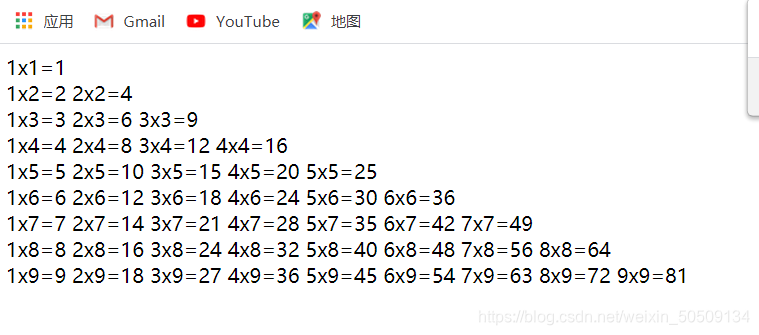
{while(cin >> x) // 循环读入待分解的数{resolve(x); // 分解因子cout<< "The total numbers is  " << num << endl; // 输出分解因子的总数cout << "--------------------------" << endl; // 输出分隔符num = 0; // 重置分解因子的总数break;}return 0;}
输出结果：

在这里插入图片描述

三、分苹果相关问题

接下来是只需要输出组合数的代码：

将要拆的数n，当作n个苹果。拆成k个数，当作k个盘子。
k > n时，多出来的盘子必定是空的，拆分情况的数量和k==n没区别。
k < n时，两种情况：
1)至少有一个空盘子，则相当于少一个盘子的情况q(n, k) = q(n, k-1)
2)没有空盘子，分配完之后相当于每个盘子里都减少一个苹果的情况q(n, k) = q(n-k, k)
两种情况合起来就是：q(n, k) = q(n, k-1) + q(n-k, k)
n的最大值为120，可以用空间换时间，用一个120*120的二维数组存储所有结果

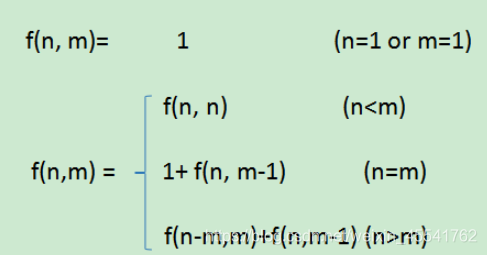
在这里插入图片描述

#include <iostream>
using namespace std;
int main()
{int solution[121][121] = {0}; // 定义一个二维数组solution，用于存储结果for (int n = 1; n <= 120; n++) // n表示苹果的个数，从1到120遍历{for (int k = 1; k <= 120; k++) // k表示盘子的个数，从1到120遍历{if (n == 1 || k == 1) // 如果苹果个数为1或盘子个数为1，那么只有一种放法{solution[n][k] = 1;}else if (n > k) // 如果苹果个数大于盘子个数，那么可以分成两种情况{// 第一种情况：至少有一个盘子不放苹果，即f(n-k,k)// 第二种情况：每个盘子都放至少一个苹果，即f(n,k-1)solution[n][k] = solution[n-k][k] + solution[n][k-1];}else if(n == k) // 如果苹果个数等于盘子个数，那么只有一种放法{// n个苹果，k-1个盘子只是比k个盘子少了一种全1的组合，即只少了一种情况solution[n][k] = 1 + solution[n][k-1];}}}int n;while (cin >> n) // 循环读入n{cout << solution[n][n] << endl; // 输出结果}return 0;
}

本题就是先建一个二维数组用以存储数据，然后根据前面的分析填充数据，然后使用输入的值查表就可以得到结果。

补充放苹果问题：

题目描述:

把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？（用K表示）5，1，1和1，5，1 是同一种分法。

输入

每个用例包含二个整数M和N。0<=m<=10，1<=n<=10。

样例输入:
7 3
样例输出:
8
解题分析：

设f(m,n)为m个苹果，n个盘子的放法数目，则先对n作讨论，

  1. 当m < n：则必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响。即 if(n>m) f(m,n) = f(m,m)
  2. 当m >= n:不同的放法可以分成两类：含有0的方案数，不含有0的方案数
  • 含有0的方案数，即有至少一个盘子空着，即相当于 f(m,n)=f(m,n-1);
  • 不含有0的方案数，即所有的盘子都有苹果，相当于可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即 f(m,n)=f(m-n,n)。

而总的放苹果的放法数目等于两者的和，即 f(m,n)=f(m,n-1)+f(m-n,n)

递归出口条件说明：
当n=1时，所有苹果都必须放在一个盘子里，所以返回1；
当m==0(没有苹果可放)时，定义为1种放法；
递归解法：

#include <iostream>
using namespace std;
int fun(int m,int n)
{if(m==0||n==1)return 1;else if(m<n)return fun(m,m);elsereturn fun(m-n,n)+fun(m,n-1);
}
int main()
{int a,b,num;while(cin >> a >> b){cout << fun(a,b) << endl;}
}
//动态归划解法：
#include <iostream>
using namespace std;
int main()
{int solution[11][11] = {0};for (int n = 0; n <= 10; n++){for (int k = 0; k <= 10; k++){if (n == 0 || k == 1){solution[n][k] = 1;}else if (n >= k){solution[n][k] = solution[n-k][k] + solution[n][k-1];}else if(n < k){solution[n][k] = solution[n][n];}                                         }}int n, k;while (cin >> n >> k){cout << solution[n][k] << endl;}return 0;
}

问题描述：将整数N分成K个整数的和且每个数大于等于A小于等于B，求有多少种分法

#include <iostream>
using namespace std;
int Dynamics(int n, int k, int min, int max)
{ //将n分为k个整数，最小的大于等于min,最大的不超过Bif(n < min)return 0;  //当剩下的比min小，则不符合要求，返回0if(n <= max && k == 1)//原来只有k==1最后一个判断条件，下面k==0也没有，//现在做这样的修改是为了处理按照要求不能分配的特殊情况return 1;if (k == 0)//在不能正确划分的情况下，防止k变为负值，提前终止！{//cout << "The value of k is " <<  k << endl;return 0;}int sum = 0;//sum直到最后把n划分完才会得到返回值1，否则递归过程中每段都返回0；如果划分成功，则最后就得到0+...+0+1等于1for(int t = min; t <= max; t++){sum += Dynamics(n-t, k-1, t, max);//为了避免重复，所以第三个参数用t,说明t是每次递归完成后是动态变化的}return sum;
}int main()
{int a, b, mins, maxs;while (cin >> a >> b >> mins >> maxs){cout << Dynamics(a, b, mins, maxs) << endl;//最开始函数的min由这里控制，//随后的min由函数内的for循环控制}
}

问题拓展：前面的放苹果问题，如果每个盘子都不能为空，则有多少种放法？
思路，先把每个盘子都放一个苹果，这样问题就转化为：m-n个苹果放进n个盘子里，盘子允许空，即为前面的问题。


http://chatgpt.dhexx.cn/article/mN1tfVtg.shtml

相关文章

js输出1-100之间所有的质数并求总个数

js输出1-100之间所有的质数并求总个数

代码如下&#xff1a; <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><meta http-equiv"X-UA-Compa…
阅读更多...
JavaScript输出杨辉三角形

JavaScript输出杨辉三角形

JavaScript输出杨辉三角形 杨辉三角形的特点和规律代码如下&#xff1a;结果 杨辉三角形的特点和规律 起始行为第0行&#xff0c;第N行为N1个数从 N > 2行开始&#xff0c;每一行的数值&#xff08;不包含两边的数值&#xff09;都是上一行两个数字的相加。当 J1 或 JN1时&…
阅读更多...
Vscode中JS输出乱码问题的解决

Vscode中JS输出乱码问题的解决

一直很好用vscode突然不好用了&#xff0c;原来输出正常的JS代码在输出中都是乱码。于是上网查答案&#xff0c;试了很多奇奇怪怪的答案&#xff0c;然而没有一款能够解决我这个问题。仔细琢磨&#xff0c;既然以前好用&#xff0c;现在不好用&#xff0c;应该是某个电脑操作“…
阅读更多...
js输出九九乘法表

js输出九九乘法表

js输出九九乘法表 控制台输出 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"wid…
阅读更多...
利用Javascript输出多个图片

利用Javascript输出多个图片

利用Javascript输出多个图片 如果不利用Js输出图片的话&#xff0c;利用HTMLCSS输出多个图片非常麻烦的&#xff0c;工作量庞大。 建议遇到有必要多个输出的图片&#xff0c;使用js是最好的方法。 <script>var i;var arr["<img src./img/1.jpg>","…
阅读更多...
js实现图形输出

js实现图形输出

1、矩形 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><body><script>//嵌套循环:外层循环一次&#xff0c;内层循环一轮//矩形for (var j 1; j < 5; j) {for (var i 1; …
阅读更多...
用JS 输出 正三角形

用JS 输出 正三角形

效果图 以下是代码及 每行代码解释&#xff0c;仅供参考。 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"view…
阅读更多...
js 页面输出html,javascript中如何输出？

js 页面输出html,javascript中如何输出？

面对刚刚学习JavaScript的同学们&#xff0c;你是否知道JavaScript如何输出&#xff1f;下面本篇文章就来给大家介绍一下javascript的几种输出方式&#xff0c;希望对大家有所帮助。 JavaScript的输出方式&#xff1a; javascript 没有任何打印或输出的函数&#xff0c;可以通过…
阅读更多...
js 向页面输出html,javascript怎么输出？

js 向页面输出html,javascript怎么输出？

JavaScript怎么输出&#xff1f;输出方式有哪些&#xff1f;下面本篇文章就给大家介绍JavaScript的几种输出方式&#xff0c;希望对大家有所帮助。 方法1&#xff1a;使用window.alert()进行输出 window.alert()方法用于显示带有一条指定消息和一个【确认】 按钮的警告框。 代码…
阅读更多...
JS 的三种输出方式

JS 的三种输出方式

输出方式 第一种&#xff1a;alert&#xff08;&#xff09; alert() 语句&#xff1a;可以输出警告框。具有弹框效果 代码示例&#xff1a; <script type"text/javascript">alert(holle warold); </script> 效果图&#xff1a; 第二种&#xff1a;…
阅读更多...
JavaScript的输出方式大全

JavaScript的输出方式大全

helo&#xff01;小伙伴们&#xff0c;你们是不是和我一样学在学js过程中感觉这个知识不仅脑子&#xff0c;反而觉得相关的知识好多呀&#xff0c;网上的文章和视频也是&#xff0c;都不知道该怎么选了&#xff0c;没关系&#xff0c;我们慢慢来&#xff0c;这些知识点一点一点…
阅读更多...
JS输出方式

JS输出方式

一个程序编写完成之后&#xff0c;我们运行出的结果也有着不同的输出方式。 下面我主要介绍三种输出结果的方式&#xff1a;alert&#xff1b;console.log&#xff1b;document.write。 alert 这种输出方式是使用弹出框显示结果&#xff0c;但是只能一个一个的输出&#xff…
阅读更多...
Android LiveData我的理解

Android LiveData我的理解

LiveData用大众语言来来讲&#xff0c;是一个被观察者&#xff0c;也是一个数据持有类或者可以称为一个数据的包裹类。它有别于其他的观察者的重点是&#xff0c;他具有生命周期感知能力&#xff0c;这里生命周期指的是activities, fragments, or services 的生命周期。 讲到L…
阅读更多...
Android LiveData组件详解以及LiveDataBus

Android LiveData组件详解以及LiveDataBus

转载请标明出处&#xff1a;https://blog.csdn.net/zhaoyanjun6/article/details/99749323 本文出自【赵彦军的博客】 文章目录 LiveData简介使用Java 使用方式两种订阅模式observeobserveForever 三、LiveDataBus3.1 为什么要用LiveDataBus替代EventBus和RxBus?3.2 LiveDataB…
阅读更多...
【Android】MutableLiveData与LiveData

【Android】MutableLiveData与LiveData

MutableLiveData笔记 MutableLiveData是什么&#xff1f;LiveData是什么&#xff1f;LiveData常用的方法MutableLiveData和LiveData的区别 关于postValue和setValue的机制简单理解 MutableLiveData是什么&#xff1f; public class MutableLiveData extends LiveData<T>…
阅读更多...
Android架构——LifeCycle和LiveData原理学习总结

Android架构——LifeCycle和LiveData原理学习总结

本文是楼主学习LifeCycle和LiveData原理的一些总结&#xff0c;本文不会长篇分析源码&#xff0c;而是利用类图和总结性的文字归纳原理。由于Livedata和LifeCycle有紧密联系&#xff0c;所以本文先总结LifeCycle原理&#xff0c;再总结LifeData原理。 本文LifeCycle基于版本an…
阅读更多...
Android架构之LiveData组件

Android架构之LiveData组件

Jetpack组件系列文章 Android架构之LifeCycle组件 Android架构之Navigation组件(一) Android架构之Navigation组件(二) Android架构之Navigation组件(三) Android架构之Navigation组件(四) Android架构之ViewModel组件 Android架构之LiveData组件 Android架构之Room组件(一) An…
阅读更多...
LiveData的基本使用

LiveData的基本使用

我们在《ViewModel的基本使用》这篇文章中提到了&#xff0c;ViewModel的主要作用是存放页面所需要的各种数据&#xff0c;而当这些数据发生变化时&#xff0c;我们采用接口的方式实现对页面的通知。 这样做是可行的&#xff0c;但如果要观察的数据很多&#xff0c;则需要定义大…
阅读更多...
DataBinding与LiveData

DataBinding与LiveData

DataBinding 一、添加配置二、使用修改布局文件具体使用单向绑定、方法绑定双向绑定、加载网络图片例子Adapter中使用使用 ObservableField 一、添加配置 如果需要使用databinding 需要在gradle中添加如下配置 defaultConfig {......//开启dataBindingdataBinding {enabled …
阅读更多...
ViewModel+LiveData+DataBinding

ViewModel+LiveData+DataBinding

1 ViewModel ViewModel要解决的问题 瞬态数据的丢失异步调用的内存泄露类膨胀提高维护难度和测试难度 ViewModel是介于视图和数据模型之间的桥梁&#xff0c;使数据和视图分离的同时还能通信。 2 LiveData ViewModel中可以存储普通数据&#xff0c;LiveDate数据 普通数据…
阅读更多...
推荐文章

Copyright @ 2022~2023