杨辉三角 算法

article/2025/9/15 0:16:28

最近，看一些东西突然碰到了杨辉三角，有点懵，故查了点资料，

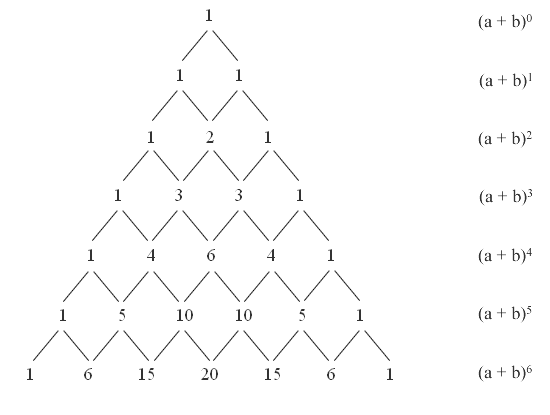
首先看一下杨辉三角形式：


首先，要想编程解决杨辉三角，必先了解其性质：



上述那么多，我们真正需要的也就是第一个，每个数等于它上方两数之和。



C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<cstdio>
#include<iostream>
using  namespace  std;
long  long  int  Triangle[1000][1000];
int  main()
{
     Triangle[1][1]=1; //初始化 
     Triangle[2][1]=1;Triangle[2][2]=1;
     for ( int  i=3;i<=50;i++) //制作三角。 
     {
         for ( int  j=1;j<=i;j++)
         {
             Triangle[i][j]=Triangle[i-1][j-1]+Triangle[i-1][j];
         }
     }
     for ( int  i=1;i<=50;i++) //输出 
     {
         for ( int  j=1;j<=i;j++)
         {
             cout<<Triangle[i][j]<< "  " ;
         }
         cout<<endl;
     }
     return  0;
}


C#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class  Program
{
   public  int  yanghui( int  value)
   {
   if (value<3)  return  1;
   int [,]arry= new  int [value,value];
   Console.WriteLine( "数组为：" );
   for ( int  i=0;i<value;i++)
   {
     string  str= "" ;
     str=str.PadLeft(value-i);
     Console.Write(str);
     for ( int  j=0;j<=i;j++)
     {
       if (i==j||j==0)
         arry[i,j]=1;
       else
         arry[i,j]=arry[i-1,j-1]+arry[i-1,j];
       Console.Write(arry[i,j]+ "" );
     }
     Console.WriteLine();
   }
}
  
static  void  Main( string []args)
{
   Program p= new  Program();
   Console.WriteLine( "请输入数组值：" );
   if  (p.yanghui(Convert.ToInt16(Console.ReadLine())))
     Console.WriteLine( "输入数值必须大于3" );
   Console.Readkey();
}
  
}



C
以下的代码均用标准 C 语言写成，可以被包括 MSVC（含 VC6）、GCC 的多种 C 编译器编译。
这个算法使用只行列位置和左侧的数值算出数值：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* yh-rt1.c - 时间和空间最优算法 */
#include <stdio.h>
#include <stdlib.h>
int  main()
{
     int  s = 1, h;                     // 数值和高度
     int  i, j;                         // 循环计数
     scanf ( "%d" , &h);                  // 输入层数
     printf ( "1\n" );                    // 输出第一个 1
     for  (i = 2; i <= h; s = 1, i++)          // 行数 i 从 2 到层高
     {
         printf ( "1 " );                 // 第一个 1
         for  (j = 1; j <= i - 2; j++)  // 列位置 j 绕过第一个直接开始循环
             //printf("%d ", (s = (i - j) / j * s));
             printf ( "%d " , (s = (i - j) * s / j));
         printf ( "1\n" );                // 最后一个 1，换行
     }
     getchar ();                        // 暂停等待
     return  0;
}
默认状态下不启用金字塔和菱形的输出 默认状态下不启用金字塔和菱形的输出
默认求直角三角形，可通过注释的开关或使用编译器的 -D 定义开关调节等腰三角形和菱形输出。如果觉得复杂，可按照 define 使用的情况剔除因不符合 ifdef 条件从而未启用的代码之后阅读。
这个算法创建了一个二维数组，并且通过上一行的数值求当前行。在反过来再次打印时，这个程序会使用以前算好的值，从而节省了重复迭代的时间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* yh-2d.c - 二维数组迭代 */
#include<stdio.h>
#define M 10       // 行数
// #define PYRAMID // 金字塔，会额外填充空格
// #define REVERSE // 反向再来一次，得到菱形
int  main( void )
{
   int  a [M][M], i, j;    // 二维数组和循环变量，a[行][列]
   for  (i = 0; i<M; i++)  // 每一行
   {
#ifdef PYRAMID
     for  (j = 0;j <= M-i; j++)  printf  ( "  " );
#endif // 填充结束
     for  (j = 0; j <= i; j++)  // 赋值打印
       printf ( "%4d" , (a[i][j] = (i == j || j == 0) ? 1 :  // 首尾置 1
         a[i - 1][j] + a[i - 1][j - 1] ));  // 使用上一行计算
     printf ( "\n" );
   }
#ifdef REVERSE
   for (i = M-2; i >= 0; i--)
   {
#ifdef PYRAMID
     for  (j = 0;j <= M - i; j++)  printf ( "  " );
#endif // 填充结束
     for  (j = 0;j <= i; j++)  printf ( "%4d" ,a[i][j]);  // 直接使用以前求得的值
     printf ( "\n" );
   }
#endif // 菱形结束
   getchar ();  // 暂停等待
}
这一个使用大数组写成，风格更接近教科书上的 VC6 代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/* yh-rt3.c - 较为暴力的大数组 */
#include <stdio.h>
#include "string.h"
int  main()
{
     int  a[10000];         //容器，由n*(n+1)/2<=10000可知，n<=141
     int  b,CR,i;         //b为当前行数，CR为要求显示的行数，i为循环数
     printf ( "请输入要显示的行数（3~141）：" );
     scanf ( "%d" ,&CR);
     YHSJ(CR);
     a[1]=a[2]=1;         //前两行数值少且全为1，故直接输出
     printf ( "%d\n" ,a[1]);
     printf ( "%d %d\n" ,a[1],a[2]);
     for (b=3;b<=CR;b++)         //从第三行开始判断
     {
         for (i=b;i>=2;i--)         //从倒数第一个数开始加
           a[i]=a[i]+a[i-1];         //杨辉三角的规律，没有值的数组默认为0
         for (i=1;i<=b;i++)         //显示循环
           printf ( "%d " ,a[i]);
         printf ( "\n" );         // 换行
     }
     return  0;
}
这个版本使用队列的方式输出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <stdlib.h>
#define EMPTY 1
#define OFLOW 2
#define INVAL 3
#define MAX_Q 100
typedef  int  DataType;  // 数据类型选择
typedef  struct { DataType elem[MAX_Q];  int  front, rear; } LinkQ;
// 队列及检查宏
#define InitQ(Q) LinkQ Q; Q.front=Q.rear=-1;
#define _EQ(Q,e) Q.elem[(Q.rear=(Q.rear+1)%MAX_Q)]=e
#define EnQ(Q,e) if((Q.rear+1)%MAX_Q==Q.front) Exit(OFLOW,"Overflow"); _EQ(Q,e)
#define DeQ(Q,e) e=Q.elem[(Q.front=(Q.front+1)%MAX_Q)]
#define Front(Q) Q.elem[(Q.front+1)%MAX_Q]
// 退出
int  Exit( int  err,  char  msg[]) {  puts (msg);  exit (err);  return  err; }
int  main( void ){
     int  n=1,i,j,k,t;
     InitQ(Q);
     printf ( "please enter a number:" );
     scanf ( "%d" ,&n);
     if  (n<=0) {
         printf ( "ERROR!\n" );
         exit (INVAL);
     }
     for (i=0;i<n;i++)  printf ( " " );
     puts ( "1" ); EnQ(Q,1); EnQ(Q,1);
     for (i=1;i<n;i++) {
         for (k=0;k<n-i;k++)  printf ( " " );
         EnQ(Q,1);
         for (j=0;j<i;j++){
             DeQ(Q,t);
             printf ( "%3d " ,t);
             EnQ(Q,t+Front(Q));
         }
         EnQ(Q,1);
         DeQ(Q,t);
         printf ( "%d\n" ,t);
     }
     return  0;
}

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public  class  TriangleArray
{
    public  static  void  main(String[] args)
    {
       final  int  NMAX =  10 ; 
       // allocate triangular array
       int [][] odds =  new  int [NMAX +  1 ][];
       for  ( int  n =  0 ; n <= NMAX; n++)
          odds[n] =  new  int [n +  1 ];  
       // fill triangular array
       for  ( int  n =  0 ; n < odds.length; n++)
          for  ( int  k =  0 ; k < odds[n].length; k++)
          {
             /*
              * compute binomial coefficient n*(n-1)*(n-2)*...*(n-k+1)/(1*2*3*...*k)
              */
             int  lotteryOdds =  1 ;
             for  ( int  i =  1 ; i <= k; i++)
                lotteryOdds = lotteryOdds * (n - i +  1 ) / i;
             odds[n][k] = lotteryOdds;
          }
       // print triangular array
       for  ( int [] row : odds)
       {
          for  ( int  odd : row)
             System.out.printf( "%4d" , odd);
          System.out.println();
       }
    }
}

PHP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
<?php
/* 默认输出十行，用T(值)的形式可改变输出行数 */
class  T{
   private  $num ;
   public  function  __construct( $var =10) {
     if  ( $var <3)  die ( "值太小啦！" );
     $this ->num= $var ;
   }
   public  function  display(){
     $n = $this ->num;
     $arr = array ();
   //$arr=array_fill(0,$n+1,array_fill(0,$n+1,0));
     $arr [1]= array_fill (0,3,0);
     $arr [1][1]=1;
     echo  str_pad ( "&nbsp;" , $n *12, "&nbsp;" );
     printf( "%3d" , $arr [1][1]);
     echo  "<br/>" ;
     for ( $i =2; $i <= $n ; $i ++){
       $arr [ $i ]= array_fill (0,( $i +2),0);
       for ( $j =1; $j <= $i ; $j ++){
         if ( $j ==1)
           echo  str_pad ( "&nbsp;" ,( $n +1- $i )*12, "&nbsp;" );
         printf( "%3d" , $arr [ $i ][ $j ]= $arr [ $i -1][ $j -1]+ $arr [ $i -1][ $j ]);
         echo  "&nbsp;&nbsp;" ;
       }
       echo "<br/>" ;
     }
   }
}
$yh = new  T();  //$yh=new T(数量);
$yh ->display();
?>
只输出数组的方式如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
<?php
$max  = 10;
$L  = [1];
var_dump( $L );
$L  = [1,1];
var_dump( $L );
$n  = 2;
while  ( $n  <=  $max  - 1){
     $oldL  =  $L ;
     $L [ $n ] = 1;
     $n ++;
     for  ( $i  = 1; $i  < count ( $oldL ); $i ++){
         $L [ $i ] =  $oldL [ $i -1] +  $oldL [ $i ];
     }
     var_dump( $L );
}
?>

Python
较为便捷，代码量较少的实现方式如下：
1
2
3
4
5
6
7
8
# -*- coding: utf-8 -*-
#!/usr/bin/env python
def  triangles():
     L  =  [ 1 ]
     while  True :
         yield  L
         L.append( 0 )
         L  =  [L[i  -  1 ]  +  L[i]  for  i  in  range ( len (L))]
该方式用到了列表生成式，理解起来较困难，下面是另一种方式：
1
2
3
4
5
6
7
8
def  triangles():
     ret  =  [ 1 ]
     while  True :
         yield  ret
         for  i  in  range ( 1 ,  len (ret)):
             ret[i]  =  pre[i]  +  pre[i  -  1 ]
         ret.append( 1 )
         pre  =  ret[:]


杨辉三角还有可以通过以下方式完成

 第一行，就是（a+b）0 = 1a0b0  = 1

第二行，就是（a+b）1 =1a1b0 +1a0b1

浅谈“杨辉三角”原理

第三行，就是 (a+b)2  =1a2b0 + 2a1b1 +1a0b2

第四行，就是（a+b）3 = 1a3b0 +3a2b1 + 3a1b2+1a0b3

第五行，就是（a+b）4  =1a4b0 + 4a3b1 +6a2b2 + 4a3b1 +1a4b0

(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)*b+C(n,2)a^(n-2)*b^2+...+C(n,n)b^n


http://chatgpt.dhexx.cn/article/pIukYAbf.shtml

相关文章

杨辉三角详解--及杨辉三角正输出与倒向输出

杨辉三角详解--及杨辉三角正输出与倒向输出

PS:再次感谢官方大大推荐的关注&#xff0c;非常非常蟹蟹啦 关于杨辉三角&#xff0c;这里引用百度百科的简介 杨辉三角&#xff0c;是二项式系数在三角形中的一种几何排列&#xff0c;中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲&#xff0c;帕斯卡&…
阅读更多...
杨辉三角里的算法

杨辉三角里的算法

文章目录 题目&#xff1a;题解&#xff1a;杨辉三角由来杨辉三角规律杨辉三角在编程实现 题目&#xff1a; 题目来源杭电ojProblem ID:2032 题解&#xff1a; 1&#xff0c;杨辉三角规律 2&#xff0c;在编程中呈现 3&#xff0c;简化思路 #include<stdio.h> int …
阅读更多...
实现杨辉三角的几种方法

实现杨辉三角的几种方法

杨辉三角&#xff1a;百度百科 方法一&#xff1a;迭代 def triangle_1(x):""":param x: 需要生成的杨辉三角行数:return:"""triangle [[1], [1, 1]] # 初始化杨辉三角n 3 # 从第三行开始计数,逐行添加while n < x:for i in range(0, n-…
阅读更多...
[TCP/IP] Linux 搭建服务器局域网

[TCP/IP] Linux 搭建服务器局域网

文章目录 [TCP/IP] Linux 搭建服务器局域网1. 使用python内置库http.server2. 使用Http-Server [TCP/IP] Linux 搭建服务器局域网 1. 使用python内置库http.server python3: http.server 命令行启动&#xff1a; # python 3 python -m http.server 8000 # python 2 python -m…
阅读更多...
Factorio异星工厂搭建服务器

Factorio异星工厂搭建服务器

环境&#xff1a;阿里云 ubuntu 按需计费1C1G的配置&#xff0c;带宽最低&#xff0c;因为就2~3人玩 参考文章&#xff1a;https://www.jianshu.com/p/01aea26df1e0 1.购买云服务器&#xff08;aliyun还要先充100才能按需计费使用&#xff09; 2. xshell 登录云服务器 3. 下载…
阅读更多...
服务器环境搭建

服务器环境搭建

服务器&#xff1a;腾讯云服务器 操作系统&#xff1a;CentOS 7.6 64bit 一、本地连接云服务器 1.本地是windows系统可下载Xshell或Putty客户端用来连接远程服务器&#xff0c;本文以Putty为例。 2.点击下载Putty&#xff0c;并安装后打开&#xff0c;并填写服务器ip&#…
阅读更多...
从零搭建服务器（图文详解，绝对无广告成分）

从零搭建服务器（图文详解，绝对无广告成分）

目录 前言 一、服务器是什么&#xff1f; 二、申请域名和服务器 1.申请域 2域名与服务器的绑定 总结 前言 本人第一次接触服务器&#xff0c;借此机会写个帖子帮助后来人学习&#xff0c;少一些迷茫&#xff0c;少浪费一些时间 一、服务器是什么&#xff1f; 服务器可以…
阅读更多...
如何从零开始搭建服务器

如何从零开始搭建服务器

文章目录 前言 记录如何将一台空服务器搭建满足开发需要。 一、Docker是什么&#xff1f; 二、Docker搭建 1.安装与配置 2.配置 Docker 容器与镜像 3.Docker 常用命令 4.GUI 管理配置 三、Docker搭建Mysql数据库 1.建立镜像 2.一般来说数据库容器不需要建立目录映射 3.连接mysq…
阅读更多...
Node 简单搭建服务器

Node 简单搭建服务器

作为前端开发能自己动手搭建一个本地服务器真的太有必要了 一. 准备Node 环境 下载安装就可以,一步一步完成,默认路径就可以,不是默认路径需要自己配置环境变量 cmd 小黑屋 输入node 二. node 如何直接运行 js 文件 node fileName 即可运行对应的文件 路径正确就ok 依赖打…
阅读更多...
动态链路聚合

动态链路聚合

客户需求&#xff1a;增加链路带宽&#xff0c;提高链路可靠性 实验步骤&#xff1a; 静态聚合的端口不与对端设备交互信息 动态聚合是双方协商&#xff0c;端口使用LACP协议与对端交互信息 聚合组中配置相同&#xff0c;端口号最小的是参考端口 #修改设备名称 <H3C>sys …
阅读更多...
Windows 10 链路聚合

Windows 10 链路聚合

Windows 10 链路聚合 自己买了一个usb的HUB网口&#xff0c;之前电脑上有有个千兆网线插在路由器上&#xff0c;于是就想着做链路聚合&#xff0c;找了很多做链路聚合的教程&#xff0c;都没有找到适合的&#xff0c;于是就自己查找了官网的知识。提取精华。分享给大家 链路聚…
阅读更多...
交换机之间的链路聚合

交换机之间的链路聚合

实训日期 2021.05.12-19 一、实训目的 通过上机实训&#xff0c;使学生掌握&#xff1a; &#xff08;1&#xff09;能够实现跨交换机上实现VLAN方法&#xff1b; &#xff08;2&#xff09;能够掌握将交换机端口分配到VLAN中的操作技巧 二、实训原理 把聚合&#xff08;绑定…
阅读更多...
各厂商-链路聚合配置

各厂商-链路聚合配置

各厂商-链路聚合配置 华为网络拓扑链路聚合配置 华三网络拓扑链路聚合配置 锐捷网络拓扑链路聚合配置 思科网络拓扑链路聚合配置 在工作中会经常遇到配置不同厂家的设备&#xff0c;此次实验主要是一些常见厂商的交换设备&#xff0c;并且只配置“负载分担模式”&#xff0c;不…
阅读更多...
链路聚合协议

链路聚合协议

链路聚合 基础知识 在企业网络中&#xff0c;所有设备的流量在转发到其他网络前都会汇聚到核心层&#xff0c;再由核心区设备转发到其他网络&#xff0c;或者转发到外网。因此&#xff0c;在核心层设备负责数据的高速交换时 &#xff0c;容易发生拥塞。在核心层部署链路聚合&a…
阅读更多...
链路聚合和LACP

链路聚合和LACP

知识重点 链路聚合链路聚合简介&#xff1a; 以太网链路聚合Eth-Trunk简称链路聚合&#xff0c;它通过将多条以太网物理链路捆绑在一起成为一条逻辑链路&#xff0c;从而实现增加链路带宽的目的。同时&#xff0c;这些捆绑在一起的链路通过相互间的动态备份&#xff0c;可以有…
阅读更多...
链路聚合（二层链路聚合划分）

链路聚合（二层链路聚合划分）

目录 前言一、端口绑定技术二、实现条件三、链路聚合的分类四、二层交换机链路聚合划分实验总结 前言 前两章我们讲的是相同vlan和不同vlan之间的通信技术&#xff0c;今天要说的是链路聚合。 一、端口绑定技术 端口绑定技术&#xff1a;链路聚合(Link Aggregation) 是将一组物…
阅读更多...
华为eNSP配置链路聚合

华为eNSP配置链路聚合

华为eNSP配置链路聚合 一、配置交换机SW1二、配置交换机SW2三、配置成功后查看如下图所示 链路聚合/链路捆绑/端口聚合/eth-channel。 采用链路聚合技术可以在不进行硬件升级的条件下&#xff0c;通过将多个物理接口捆绑为一个逻辑接口&#xff0c;来达到增加链路带宽的目的。在…
阅读更多...
链路聚合，链路聚合是什么意思

链路聚合，链路聚合是什么意思

链路聚合是将两个或更多数据信道结合成一个单个的信道,该信道以一个单个的更高带宽的逻辑链路出现。链路聚合一般用来连接一个或多个带宽需求大的设备&#xff0c;例如连接骨干网络的服务器或服务器群。 　　如果聚合的每个链路都遵循不同的物理路径,则聚合链路也提供冗余和容错…
阅读更多...
链路聚合的原理以及配置

链路聚合的原理以及配置

链路聚合的原理以及配置 一、链路聚合的概述二、链路聚合的原理三、链路聚合的配置 一、链路聚合的概述 链路聚合&#xff08;Link Aggregation&#xff09; 是将两个或更多数据信道结合成一个单个的信道&#xff0c;该信道以一个单个的更高带宽的逻辑链路出现。链路聚合一般用…
阅读更多...
eNSP链路聚合

eNSP链路聚合

链路聚合原理 逻辑链路的带宽增加了大约(n-1)倍&#xff0c;这里&#xff0c;n为聚合的路数。另外&#xff0c;聚合后&#xff0c;可靠性大大提高&#xff0c;因为&#xff0c;n条链路中只要有一条可以正常工作&#xff0c;则这个链路就可以工作。除此之外&#xff0c;链路聚合…
阅读更多...
推荐文章

Copyright @ 2022~2023