numpy.meshgrid(*xi, copy=True, sparse=False, indexing='xy')
return: X1, X2,..., XN

其中 *xi = x1, x2,..., xn 都表示一维 array。


我们从下面这个简单的例子来看 meshgrid 做了什么：

import numpy as npa = np.array([2, 4, 8])
b = np.array([3, 6])x, y = np.meshgrid(a, b)

x
"""
array([[2, 4, 8],[2, 4, 8]])
"""

y
"""
array([[3, 3, 3],[6, 6, 6]])
"""

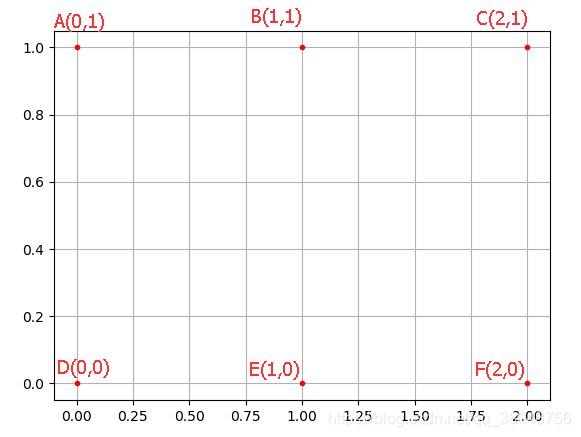
对于输入的两个一维 array a 和 b，meshgrid 返回以 ( a 中的元素, b中的元素) 为坐标点的所有可能组合，但是将两个坐标轴的坐标分开存储。上例中 x 和 y 实际上代表了 6 个坐标点：

(2, 3), (4, 3), (8, 3), (2, 6), (4, 6), (8, 6)

返回值也可以这样理解：

• x 相当于把 a 重复了 len(b) 次；
• y 相当于 b 中的每个元素重复了 len(a) 次；
• 最终形状都为 (len(b), len(a))

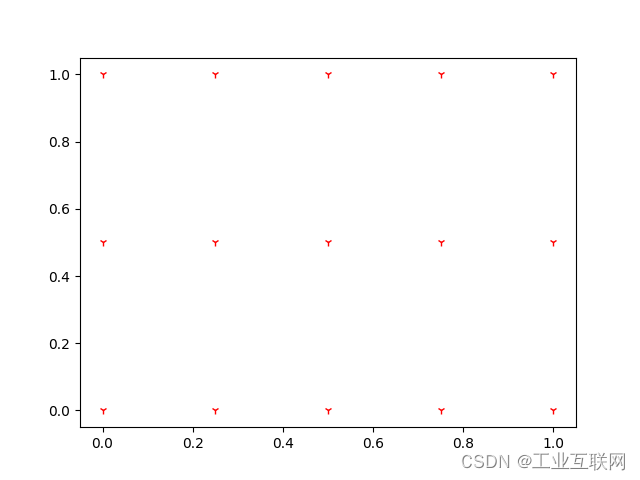
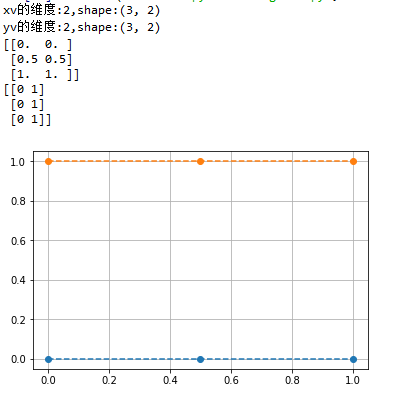
我们将 `meshgrid` 生成的坐标点在网格上画出来，就是下面这样：

plt.plot(x, y, 'rs ')
plt.grid(True)
plt.show()

x 和 y 其实就是描述这个网格上点的坐标矩阵：

$$\mathbf{X}=\left[\begin{array}{ccc}2& 4& 8\\ 2& 4& 8\end{array}\right]$$

$$\mathbf{Y}=\left[\begin{array}{ccc}3& 3& 3\\ 6& 6& 6\end{array}\right]$$

---

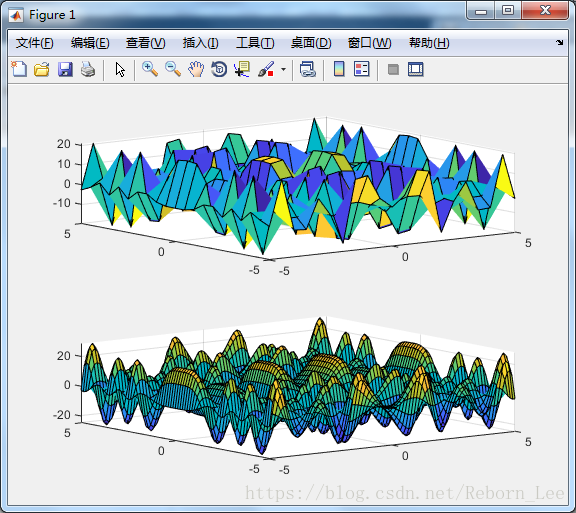
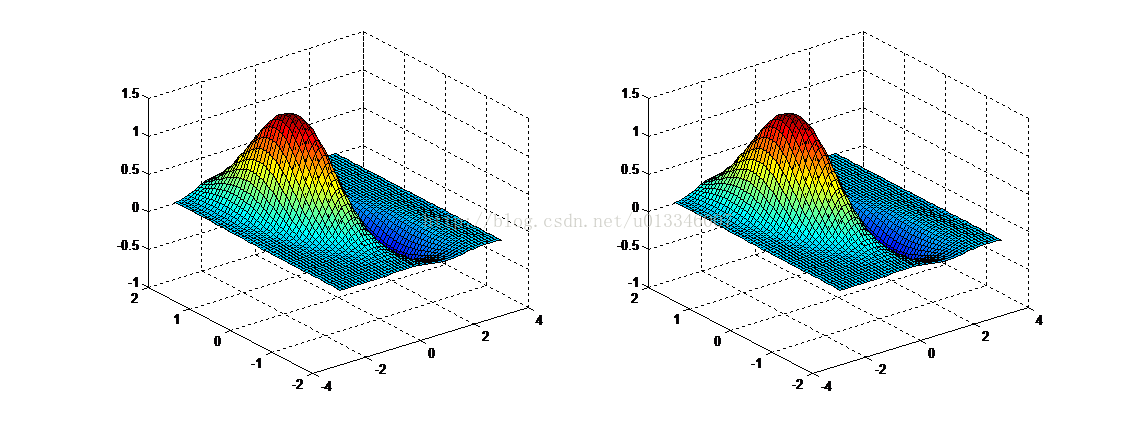
meshgrid 对于计算 grid 上的函数非常有用，例如，如果我们想要估计下面的函数在一个 grid 上一系列点的值

$$\sqrt{x^2+y^2}$$

points = np.arange(-5, 5, 0.01) # 1000 equally spaced pointsxs, ys = np.meshgrid(points, points)

xs
"""
array([[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],...,[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99],[-5.  , -4.99, -4.98, ...,  4.97,  4.98,  4.99]])
"""

ys
"""
array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],[-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],[-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],...,[ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],[ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],[ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])
"""

z = np.sqrt(xs ** 2 + ys ** 2)
z.shape
"""
(1000, 1000)
"""

我们可以画出这个图：

import matplotlib.pyplot as pltplt.imshow(z)
plt.colorbar()
plt.title('Image plot of $\sqrt{x^2 + y^2}$ for a grid of values')