1.meshgrid函数介绍

参数：
*xi，也就是x1，x2，…，xn ：表示网格坐标的一维数组。
copy：默认为True，如果为False，就返回原始数组以节省内存。
sparse：默认值为False如果为True，则返回一个稀疏网格以节省内存。
indexing：输出的笛卡尔（默认为“ xy”）或矩阵（“ ij”）索引。（后面有例子介绍该参数）

return ：返回网格坐标矩阵（返回值为list,list中包含各个方向的坐标矩阵）

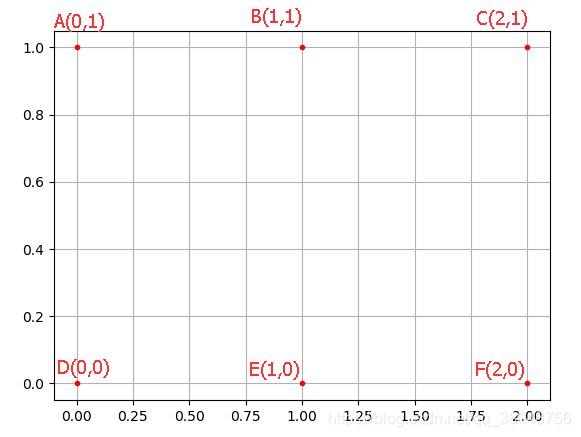
看到这可能还不是很理解，举个例子就很明白了，如下图所示，下图二维平面中有6个网格坐标，可以看出他们的横坐标为[0, 1, 2]，纵坐标为[0, 1]，倘若只知道他们的横坐标和纵坐标的一维数组，怎么构建这6个网格坐标，meshgrid的作用就是这个。

>>> a = [0, 1, 2]
>>> b = [0, 1]
>>> np.meshgrid(a,b)
[array([[0, 1, 2],[0, 1, 2]]), array([[0, 0, 0],[1, 1, 1]])]
>>>

返回的结果现在还不是6个点的坐标，但是将a中的元素与b中的每个元素一一对应就得到了上述6个点的坐标。

那么indexing的作用是什么呢？

>>> np.meshgrid(a,b,indexing = 'ij')
[array([[0, 0], [1, 1],[2, 2]]), array([[0, 1],[0, 1], [0, 1]])]
>>>

也就是若indexing = ‘xy’，返回的矩阵形状为(N2, N1, N3,…Nn)，其中Ni = len(xi)。若indexing = ‘ij’，则返回的矩阵形状为(N1, N2, N3,…Nn)。具体的影响就是处理数据时，读取数据方式不同。

 xv, yv = np.meshgrid(x, y, sparse=False, indexing='ij')for i in range(nx):for j in range(ny):# treat xv[i,j], yv[i,j]xv, yv = np.meshgrid(x, y, sparse=False, indexing='xy')for i in range(nx):for j in range(ny):# treat xv[j,i], yv[j,i]

sparse为True时，返回稀疏的网格（为了节省内存），也就是该坐标矩阵下的元素有哪些（由于每行/列下的元素都一样，所以返回一行或一列就可以知道该坐标矩阵下的元素）。

>>> x = np.meshgrid(a,b,sparse= True)
>>> x
[array([[0, 1, 2]]), array([[0],[1]])]
>>>

接下来把meshgrid的结果变为最终的坐标点：

>>> a = [0, 1, 2]
>>> b = [0, 1]
>>> np.meshgrid(a,b)
[array([[0, 1, 2],[0, 1, 2]]), array([[0, 0, 0],[1, 1, 1]])]
>>> x, y = np.meshgrid(a,b)
>>> x.flatten()[:, np.newaxis]
array([[0],[1],[2],[0],[1],[2]])
>>> y.flatten()[:, np.newaxis]
array([[0],[0],[0],[1],[1],[1]])
>>> xx = x.flatten()[:, np.newaxis]
>>> yy = y.flatten()[:, np.newaxis]
>>> np.c_[xx, yy]
array([[0, 0],[1, 0],[2, 0],[0, 1],[1, 1],[2, 1]])
>>>

---

np.newaxis介绍：可以在数组索引中使用np.newaxis对象添加大小为1的新尺寸，如：

>>> a.shape
(5, 7)
>>> a[:,np.newaxis,:].shape
(5, 1, 7)>>> x = np.arange(5)
>>> x[:, np.newaxis]
array([[0],[1],[2],[3],[4]])
>>>

np.flatten()介绍:
原型声明：def flatten(self, order='C'):

Parameters：
order{‘C’, ‘F’, ‘A’, ‘K’}, optional
“ C”表示按行优先（C样式）的顺序展平。“ F”表示按列主（Fortran样式）的顺序展平。“ A”表示如果a在内存中是连续的，则按列优先顺序进行展平；否则，按行优先进行展平。“ K”表示按元素在内存中出现的顺序展平 。默认值为“ C”。
Returns
返回展平为一维的数组副本。

---

2.meshgrid函数官方说明

meshgrid的官方api

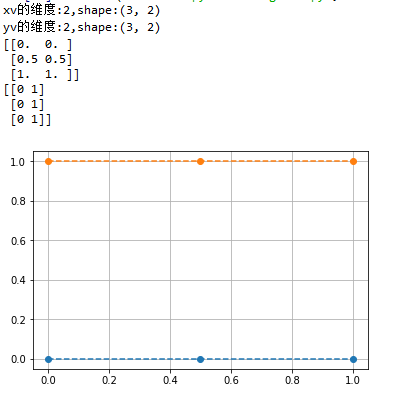
def meshgrid(*xi, copy=True, sparse=False, indexing='xy'):"""Return coordinate matrices from coordinate vectors.Make N-D coordinate arrays for vectorized evaluations ofN-D scalar/vector fields over N-D grids, givenone-dimensional coordinate arrays x1, x2,..., xn... versionchanged:: 1.91-D and 0-D cases are allowed.Parameters----------x1, x2,..., xn : array_like1-D arrays representing the coordinates of a grid.indexing : {'xy', 'ij'}, optionalCartesian ('xy', default) or matrix ('ij') indexing of output.See Notes for more details... versionadded:: 1.7.0sparse : bool, optionalIf True a sparse grid is returned in order to conserve memory.Default is False... versionadded:: 1.7.0copy : bool, optionalIf False, a view into the original arrays are returned in order toconserve memory.  Default is True.  Please note that``sparse=False, copy=False`` will likely return non-contiguousarrays.  Furthermore, more than one element of a broadcast arraymay refer to a single memory location.  If you need to write to thearrays, make copies first... versionadded:: 1.7.0Returns-------X1, X2,..., XN : ndarrayFor vectors `x1`, `x2`,..., 'xn' with lengths ``Ni=len(xi)`` ,return ``(N1, N2, N3,...Nn)`` shaped arrays if indexing='ij'or ``(N2, N1, N3,...Nn)`` shaped arrays if indexing='xy'with the elements of `xi` repeated to fill the matrix alongthe first dimension for `x1`, the second for `x2` and so on.Notes-----This function supports both indexing conventions through the indexingkeyword argument.  Giving the string 'ij' returns a meshgrid withmatrix indexing, while 'xy' returns a meshgrid with Cartesian indexing.In the 2-D case with inputs of length M and N, the outputs are of shape(N, M) for 'xy' indexing and (M, N) for 'ij' indexing.  In the 3-D casewith inputs of length M, N and P, outputs are of shape (N, M, P) for'xy' indexing and (M, N, P) for 'ij' indexing.  The difference isillustrated by the following code snippet::xv, yv = np.meshgrid(x, y, sparse=False, indexing='ij')for i in range(nx):for j in range(ny):# treat xv[i,j], yv[i,j]xv, yv = np.meshgrid(x, y, sparse=False, indexing='xy')for i in range(nx):for j in range(ny):# treat xv[j,i], yv[j,i]In the 1-D and 0-D case, the indexing and sparse keywords have no effect.See Also--------index_tricks.mgrid : Construct a multi-dimensional "meshgrid"using indexing notation.index_tricks.ogrid : Construct an open multi-dimensional "meshgrid"using indexing notation.Examples-------->>> nx, ny = (3, 2)>>> x = np.linspace(0, 1, nx)>>> y = np.linspace(0, 1, ny)>>> xv, yv = np.meshgrid(x, y)>>> xvarray([[0. , 0.5, 1. ],[0. , 0.5, 1. ]])>>> yvarray([[0.,  0.,  0.],[1.,  1.,  1.]])>>> xv, yv = np.meshgrid(x, y, sparse=True)  # make sparse output arrays>>> xvarray([[0. ,  0.5,  1. ]])>>> yvarray([[0.],[1.]])`meshgrid` is very useful to evaluate functions on a grid.>>> import matplotlib.pyplot as plt>>> x = np.arange(-5, 5, 0.1)>>> y = np.arange(-5, 5, 0.1)>>> xx, yy = np.meshgrid(x, y, sparse=True)>>> z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)>>> h = plt.contourf(x,y,z)>>> plt.show()"""