一、学习内容：

• 灰色关联分析的基本思想
• 运用灰色关联分析的基本步骤
• 灰色关联分析代码实现(Matlab)

---

二、学习时间：

2020.12.11

---

三、学习产出：

3.1 灰色关联分析基本思想

3.2 运用灰色关联分析的基本步骤

1. 确定分析数列
   • 母序列(又称参考数列，母指标)：能反映系统行为特征的数据序列——>类似与因变量Y
   • 子序列(又称比较数列，子指标)：影响系统行为的因素组成的数据序列——>类似与自变量X
2. 对变量进行预处理(去量纲，缩小变量范围，简化计算)，先求出每个指标列的均值，再用该指标列的每一个元素都除以该指标列的均值
3. 用子序列中每一个元素减去对应母序列中同一行的那个元素，并取绝对值，由此得到一个新矩阵new_X。
4. 记a为矩阵中的最小元素，b为矩阵中的最大元素，分辨系数ro通常为0.5，那么每一个元素对应母序列的关联系数为 a+ro*b./(new_X+ro*b)
5. 然后，我们再对得到的关联系数矩阵求每一列均值，得到的最后结果gamma就是每一个指标对于母序列的灰色关联度

3.3 灰色关联分析代码实现(Matlab)

3.3.1 应用一：分析产业对GDP的影响程度

数据：

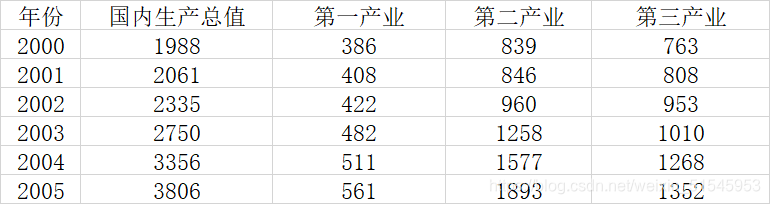
由于第一产业、第二产业、第三产业的量纲相同，去量纲步骤可以跳过。大家在使用时需要注意自己的数据量纲是否相同。

%% 应用一：分析产业对GDP的影响程度
clear;clc;
load data.mat;
r = size(data,1);
c = size(data,2);
%第一步，对变量进行预处理，消除量纲的影响（大家在使用时需要注意自己的数据量纲是否相同）
%avg = repmat(mean(data),r,1);
%data = data./avg;
%定义母序列和子序列
Y = data(:,1); %母序列
X = data(:,2:c); %子序列
Y2 = repmat(Y,1,c-1); %把母序列向右复制到c-1列
absXi_Y = abs(X-Y2)
a = min(min(absXi_Y)) %全局最小值
b = max(max(absXi_Y)) %全局最大值
ro = 0.5; %分辨系数取0.5
gamma = (a+ro*b)./(absXi_Y+ro*b) %计算子序列中各个指标与母序列的关联系数
disp("子序列中各个指标的灰色关联度分别为：");
ans = mean(gamma)

输出结果为：

子序列中各个指标的灰色关联度分别为：ans =0.7319    0.8983    0.8518

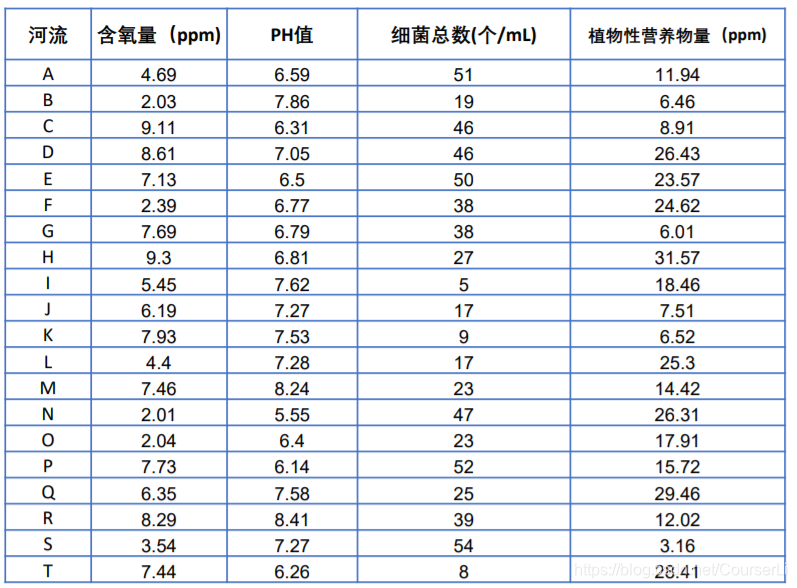
3.3.2 应用二：灰色关联分析评价河流情况

数据：

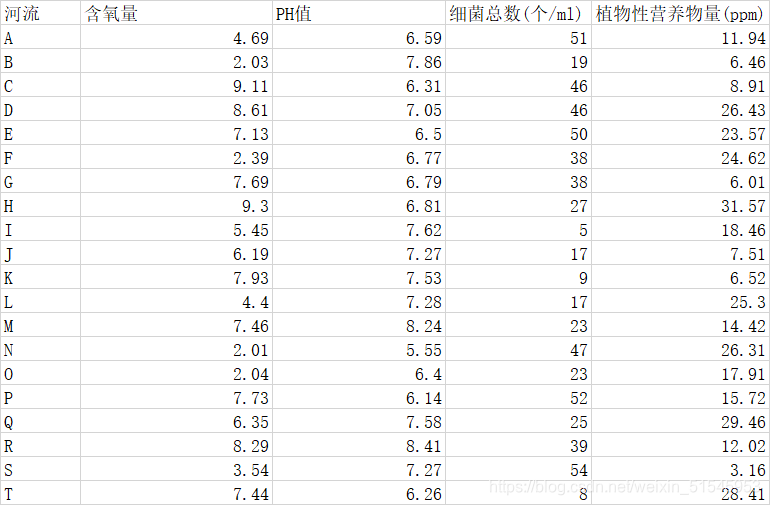
%应用二：灰色关联分析评价河流情况
clear;clc;
load X.mat;
%获取行数列数
r = size(X,1);
c = size(X,2);
%首先，把我们的原始指标矩阵正向化
%第二列中间型--->极大型
middle = input("请输入最佳的中间值：");
M = max(abs(X(:,2)-middle));
for i=1:rX(i,2) = 1-abs(X(i,2)-middle)/M;
end
%第三列极小型--->极大型
max_value = max(X(:,3)); 
X(:,3) = abs(X(:,3)-max_value);
%第四列区间型--->极大型
a = input("请输入区间的下界：");
b = input("请输入区间的下界：");
M = max(a-min(X(:,4)),max(X(:,4))-b);
for i=1:rif (X(i,4)<a)X(i,4) = 1-(a-X(i,4))/M;elseif (X(i,4)<=b&&X(i,4)>=a)X(i,4) = 1;elseX(i,4) = 1-(X(i,4)-b)/M;end
end
disp("正向化后的矩阵为：");
disp(X);
%把正向化后的矩阵进行预处理，消除量纲的影响
avg = repmat(mean(X),r,1);
new_X = X./avg;
%将预处理后的矩阵每一行的最大值取出，当成母序列(虚构的)
Y = max(new_X,[],2);
%计算各个指标和母序列的灰色关联度
%先把new_X矩阵所有元素都减去母序列中同行的元素，并取绝对值
Y2 = repmat(Y,1,c);
new_X = abs(new_X-Y2);
a = min(min(new_X)); %全矩阵最小值
b = max(max(new_X)); %全矩阵最大值
ro = 0.5;
new_X = (a+ro*b)./(new_X+ro*b);
disp("各个指标对于母序列的灰色关联度为：");
gamma = mean(new_X)
%计算各个指标的权重
disp("各个指标的权重为：");
weight = gamma./(sum(gamma,2))
%-------------------------------------------------------------------------------------------------------
%继续TOPSIS的步骤：对正向化后的矩阵X进行标准化（原矩阵除以每一列元素平方之和的开方）
temp1 = X.*X;               %先让每每一个元素平方
temp2 = sum(temp1);         %再对每一列求和
temp3 = temp2.^0.5;         %再把结果开方
temp4 = repmat(temp3,r,1);  %把开方后的结果按行复制r行
disp("******标准化后的矩阵为：");
Z = X./temp4               %原矩阵除以每一列元素平方之和的开方
Z_max = max(Z)           %获得Z每一列中最大的元素
Z_min = min(Z)           %获得Z每一列中最小的元素
D_max = sum(weight.*(Z-repmat(Z_max,r,1)).^2,2).^0.5
D_min = sum(weight.*(Z-repmat(Z_min,r,1)).^2,2).^0.5
disp("该矩阵得分为：")
S = D_min./(D_max+D_min)
disp("矩阵归一化后得分为：");
S = S./(repmat(sum(S),r,1))

输出结果为：

请输入最佳的中间值：7
请输入区间的下界：10
请输入区间的上界：20
正向化后的矩阵为：4.6900    0.7172    3.0000    1.00002.0300    0.4069   35.0000    0.69409.1100    0.5241    8.0000    0.90588.6100    0.9655    8.0000    0.44437.1300    0.6552    4.0000    0.69142.3900    0.8414   16.0000    0.60077.6900    0.8552   16.0000    0.65519.3000    0.8690   27.0000         05.4500    0.5724   49.0000    1.00006.1900    0.8138   37.0000    0.78487.9300    0.6345   45.0000    0.69924.4000    0.8069   37.0000    0.54197.4600    0.1448   31.0000    1.00002.0100         0    7.0000    0.45462.0400    0.5862   31.0000    1.00007.7300    0.4069    2.0000    1.00006.3500    0.6000   29.0000    0.18248.2900    0.0276   15.0000    1.00003.5400    0.8138         0    0.40887.4400    0.4897   46.0000    0.2731new_X =0.7831    1.2228    0.1345    1.49970.3390    0.6937    1.5695    1.04081.5211    0.8936    0.3587    1.35841.4376    1.6461    0.3587    0.66621.1905    1.1170    0.1794    1.03690.3991    1.4345    0.7175    0.90081.2840    1.4580    0.7175    0.98251.5528    1.4815    1.2108         00.9100    0.9759    2.1973    1.49971.0336    1.3874    1.6592    1.17691.3241    1.0817    2.0179    1.04860.7347    1.3757    1.6592    0.81271.2456    0.2469    1.3901    1.49970.3356         0    0.3139    0.68180.3406    0.9994    1.3901    1.49971.2907    0.6937    0.0897    1.49971.0603    1.0229    1.3004    0.27351.3842    0.0470    0.6726    1.49970.5911    1.3874         0    0.61311.2423    0.8348    2.0628    0.4096Y2 =1.4997    1.4997    1.4997    1.49971.5695    1.5695    1.5695    1.56951.5211    1.5211    1.5211    1.52111.6461    1.6461    1.6461    1.64611.1905    1.1905    1.1905    1.19051.4345    1.4345    1.4345    1.43451.4580    1.4580    1.4580    1.45801.5528    1.5528    1.5528    1.55282.1973    2.1973    2.1973    2.19731.6592    1.6592    1.6592    1.65922.0179    2.0179    2.0179    2.01791.6592    1.6592    1.6592    1.65921.4997    1.4997    1.4997    1.49970.6818    0.6818    0.6818    0.68181.4997    1.4997    1.4997    1.49971.4997    1.4997    1.4997    1.49971.3004    1.3004    1.3004    1.30041.4997    1.4997    1.4997    1.49971.3874    1.3874    1.3874    1.38742.0628    2.0628    2.0628    2.0628new_X =0.7166    0.2769    1.3651         01.2306    0.8758         0    0.52870    0.6275    1.1624    0.16270.2085         0    1.2873    0.97990    0.0735    1.0111    0.15361.0354         0    0.7170    0.53360.1739         0    0.7405    0.47550    0.0714    0.3421    1.55281.2873    1.2214         0    0.69760.6256    0.2718         0    0.48230.6938    0.9362         0    0.96930.9245    0.2835         0    0.84650.2541    1.2528    0.1095         00.3462    0.6818    0.3679         01.1591    0.5003    0.1095         00.2090    0.8060    1.4100         00.2402    0.2775         0    1.02700.1155    1.4526    0.8270         00.7963         0    1.3874    0.77430.8205    1.2280         0    1.6532各个指标对于母序列的灰色关联度为：gamma =0.6665    0.6800    0.7052    0.6880各个指标的权重为：weight =0.2433    0.2482    0.2574    0.2511******标准化后的矩阵为：Z =0.1622    0.2483    0.0245    0.30650.0702    0.1408    0.2863    0.21270.3150    0.1814    0.0655    0.27760.2977    0.3342    0.0655    0.13610.2466    0.2268    0.0327    0.21190.0826    0.2912    0.1309    0.18410.2659    0.2960    0.1309    0.20080.3216    0.3008    0.2209         00.1885    0.1981    0.4009    0.30650.2141    0.2817    0.3027    0.24050.2742    0.2196    0.3682    0.21430.1522    0.2793    0.3027    0.16610.2580    0.0501    0.2536    0.30650.0695         0    0.0573    0.13930.0705    0.2029    0.2536    0.30650.2673    0.1408    0.0164    0.30650.2196    0.2077    0.2373    0.05590.2867    0.0095    0.1227    0.30650.1224    0.2817         0    0.12530.2573    0.1695    0.3763    0.0837Z_max =0.3216    0.3342    0.4009    0.3065Z_min =0.0695         0         0         0D_max =0.21090.17390.18700.19070.20340.19200.15060.17940.09440.08410.07880.12310.16310.28390.15870.21920.17080.21530.24480.1427D_min =0.20280.19340.20810.21480.17870.18440.21370.22470.27950.25080.26190.22700.22230.07560.22440.19520.17740.19740.15590.2322该矩阵得分为：S =0.49020.52650.52660.52970.46770.48990.58660.55590.74760.74890.76860.64830.57680.21040.58570.47100.50950.47820.38910.6194矩阵归一化后得分为：S =0.04490.04820.04820.04850.04280.04480.05370.05090.06840.06850.07030.05930.05280.01930.05360.04310.04660.04380.03560.0567

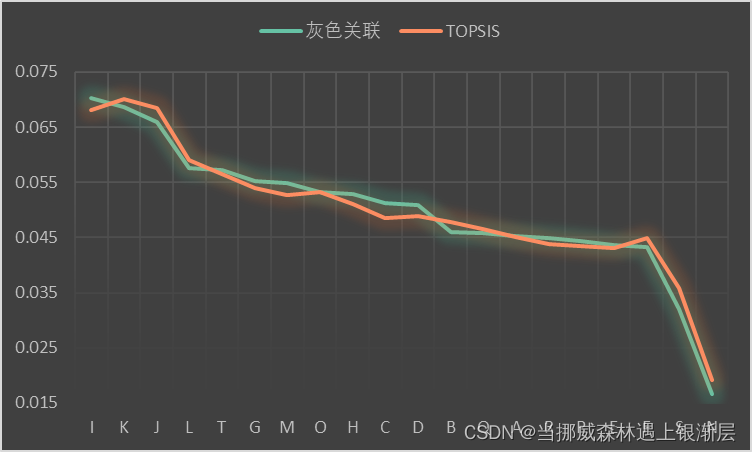
③灰色关联分析+TOPSIS和熵权法+TOPSIS计算数据得分的效果对比

3.4 补充：如何导入数据

由于很多人使用我代码的时候不知道怎么将数据替换为自己的数据，所以特地补充了一个小节来说一下怎么将数据替换成自己的。

首先，打开matlab，创建一个新的.m文件，将代码复制进去

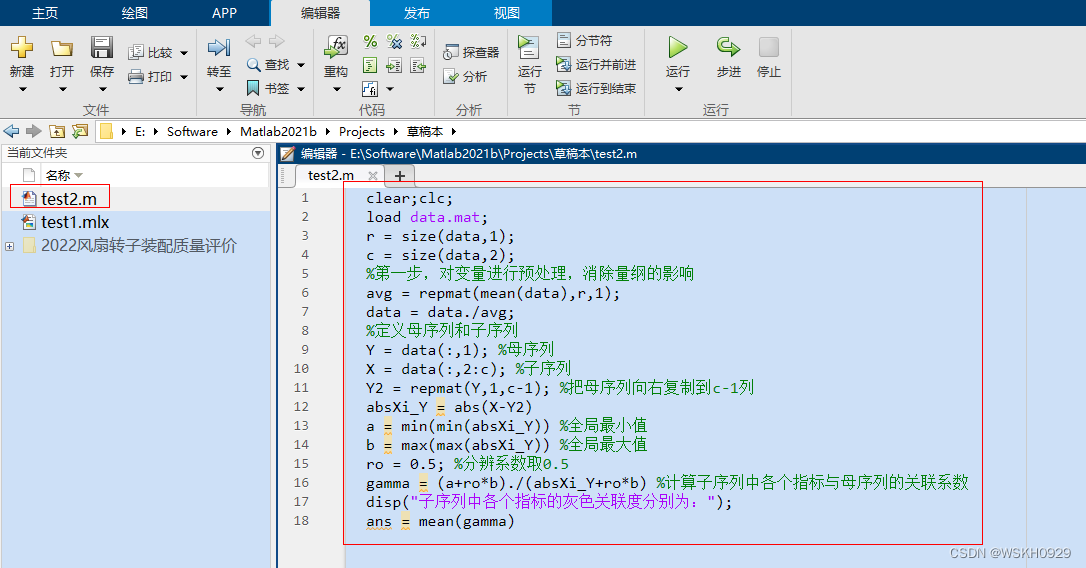
在工作区，右键，点击新建

将变量命名为data

双击刚刚新建好的data变量，进入变量内部（在此界面，可以手动编辑变量的值）

打开自己的数据（一般都是excel吧），我准备了一些例子，如下图所示（注意，年份那一列不能是横着的，否则会有问题）
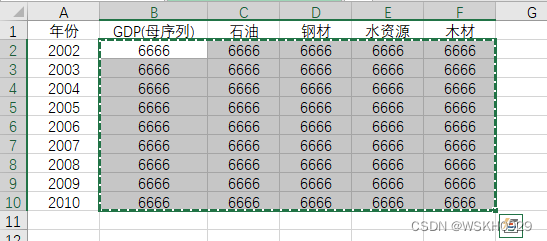
下面是正确示范：

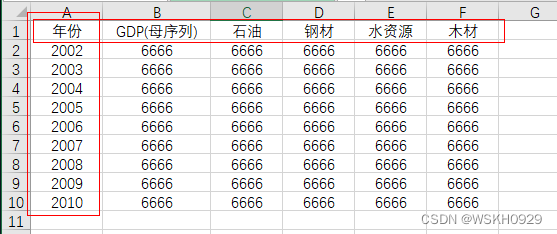
下面是错误示范：

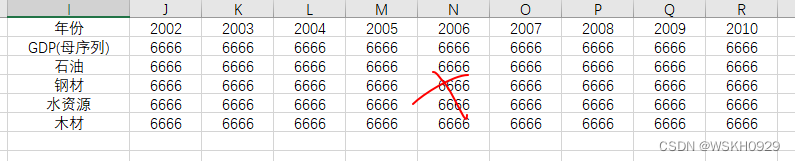
然后，复制(ctrl+c或者右键->复制)除题头外的数据

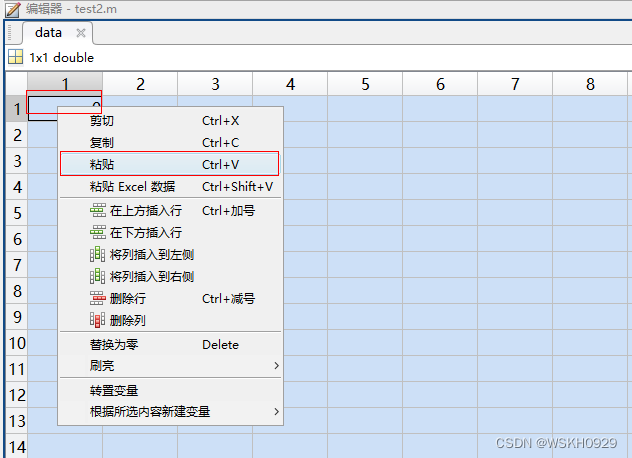
在matlab中的变量内部的左上角，右键->粘贴


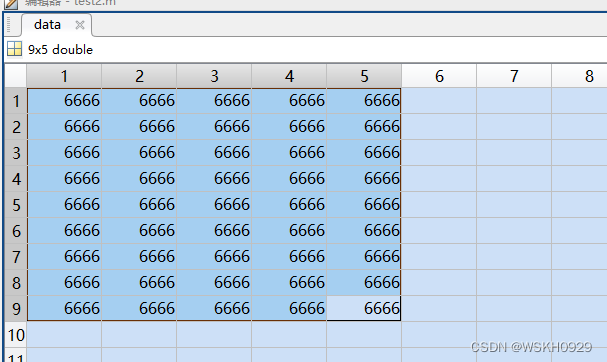
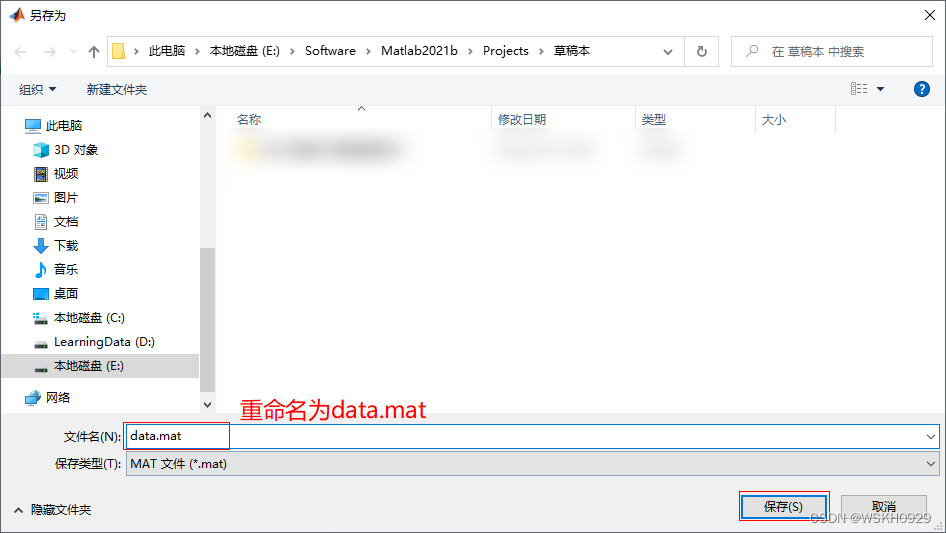
将变量data另存为data.mat文件（注意：需要存在和你代码的同一目录下）



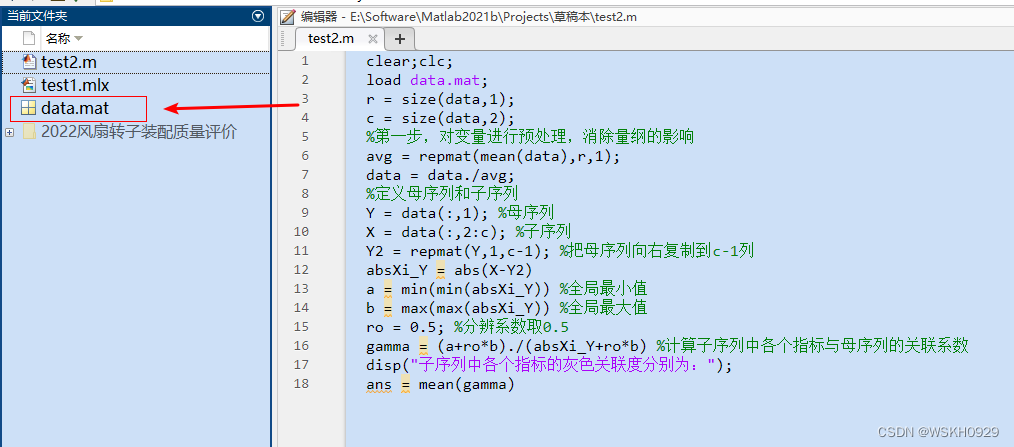
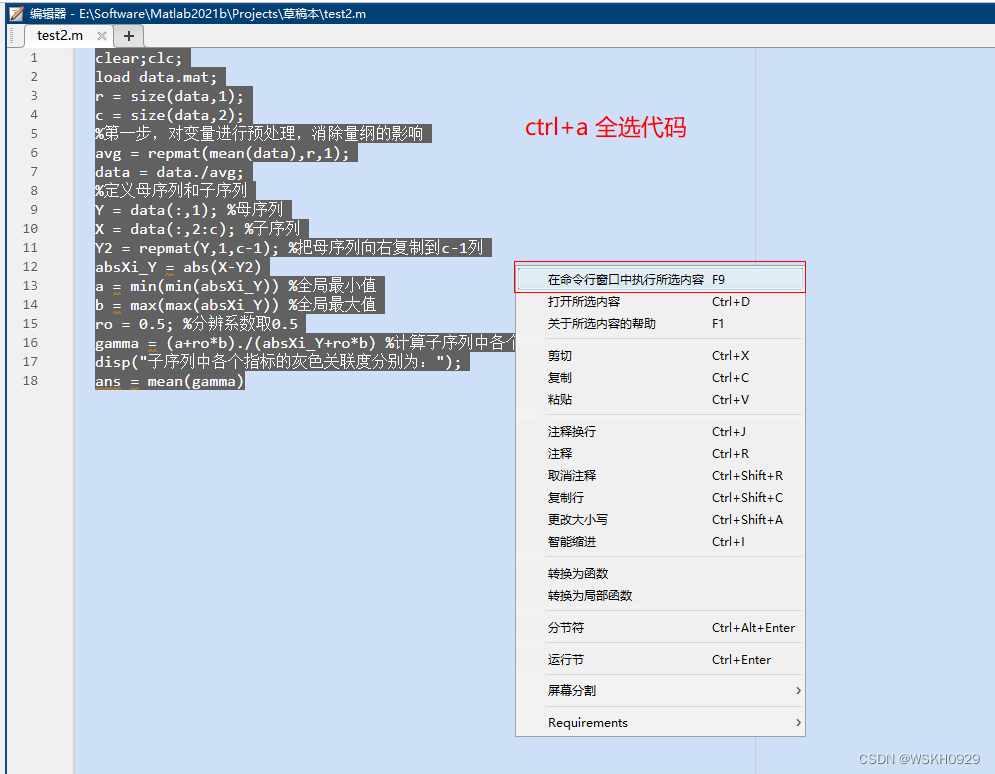
然后就可以全选代码，右键运行啦！

---

3.5 总结

• 灰色关联分析法的优势在于，它弥补了采用数理统计方法系统分析所导致的缺憾，对样本量的多少和样本有无规律都适用，而且计算量小，十分方便，更不会出现与定性结果不符合的情况。
• 但是灰色关联分析仅在我国有部分学者使用，在国际上并没有得到太多认可，而且当数据量较大的时候，使用标准化回归的方法是更好的选择，只有在数据很少万不得已的情况下，才考虑灰色关联分析，当然，你也可以两者综合考虑。
• 值得一提的是，在灰色关联分析中，母序列有多个的情况，我们只需要分开计算即可，也就是说，每一个母序列，都对应一个完整的子序列。