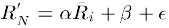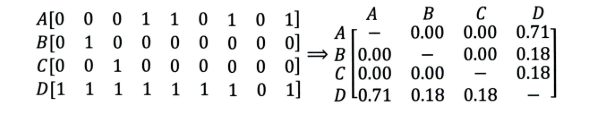简介

公司给了一个任务，要求根据相似度匹配给教师推荐课程。正好复(预)习一下协同过滤算法。直接探索一下协同过滤应用。

目前教师档案大数据系统中存有海量的教师数据，这些数据对于教师的未来决策，预测教师发展路径，推荐教师课程等有非常广泛的应用。本节，将使用数据库中的研修学分信息表中数据，基于教师的相似度，给教师推荐研修课程。

理论介绍

协同过滤算法简介

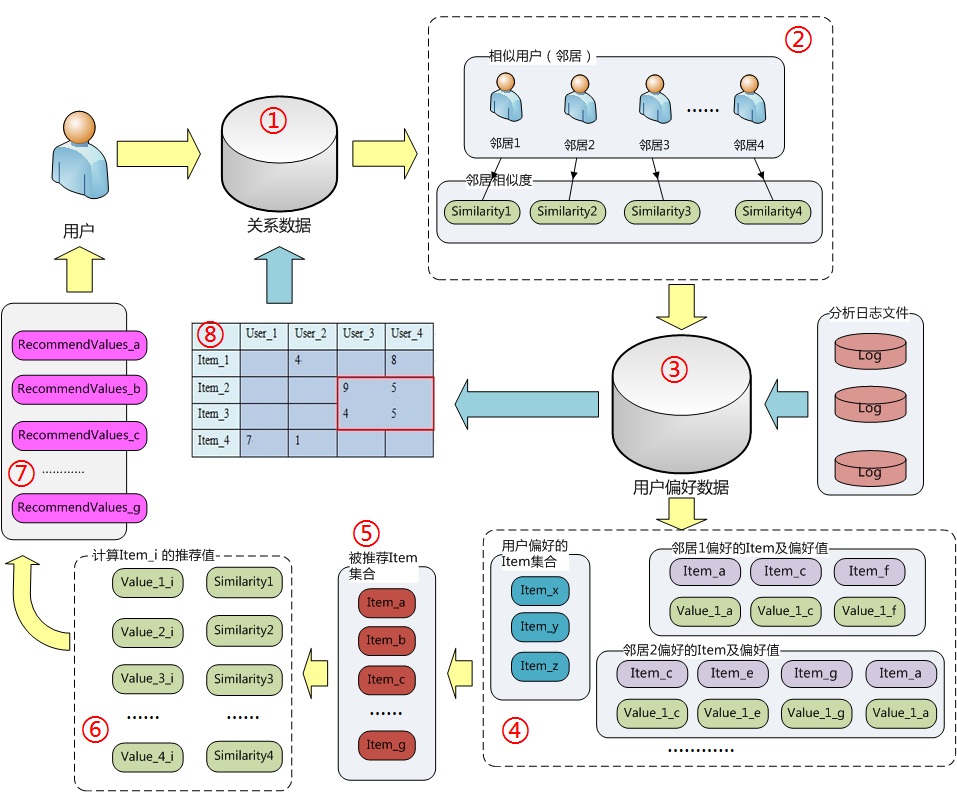
在推荐系统的众多方法之中，基于用户的协同过滤是诞最早的，原理也比较简单。基于协同过滤的推荐算法被广泛的运用在推荐系统中，比如影视推荐、猜你喜欢等、邮件过滤等。该算法1992年提出并用于邮件过滤系统，两年后1994年被 GroupLens 用于新闻过滤。一直到2000年，该算法都是推荐系统领域最著名的算法。

协同过滤简单来说是利用某兴趣相投、拥有共同经验之群体的喜好来推荐用户感兴趣的信息，个人通过合作的机制给予信息相当程度的回应（如评分）并记录下来以达到过滤的目的进而帮助别人筛选信息，回应不一定局限于特别感兴趣的，特别不感兴趣信息的纪录也相当重要。

例如，当用户A需要个性化推荐的时候，可以先找到和他兴趣详细的用户集群G，然后把G喜欢的并且A没有的商品推荐给A，这就是基于用户的协同过滤。
根据上述原理，我们可以将算法分为两个步骤：

找到与目标兴趣相似的用户集群
找到这个集合中用户喜欢的、并且目标用户没有听说过的商品推荐给目标用户。

常用的相似度计算方法

目前，机器学习中，最常用的样本相似度度量方法有以下几种：
欧式距离（Euclidean Distance）
余弦相似度（Cosine）
皮尔逊相关系数（Pearson）
修正余弦相似度（Adjusted Cosine）
汉明距离（Hamming Distance）
曼哈顿距离（Manhattan Distance）

欧式距离（Euclidean Distance）

其中最经典的是是使用欧式距离（Euclidean Distance）的欧几里得相似度。欧式距离全称是欧几里距离，是最易于理解的一种距离计算方式，源自欧式空间中两点间的距离公式。
欧几里得相似度根据欧几里得距离计算而来，距离越近相似度越高，反之相反。

平面空间内的 $a(x_{1},y_{1})$ 与 $b(x_{2},y_{2})$ 间的欧氏距离：
$d=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$

三维空间里的欧氏距离：
$d=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}$

拓展到多维空间（即实际情况中，需要计算多个课程与教师的匹配度情况）的欧式距离：
$d_{xy}=\sqrt{\sum_{i=1}^{n} (x_{i}-y_{i})^{2}}$

欧几里得相似度公式为：
$sim(x,y)=\frac{1}{1+d(x,y)}$

余弦相似度（Cosine）

在这次的实际应用中，我们采用的是余弦相似度（Cosine）。
首先，样本数据的夹角余弦并不是真正几何意义上的夹角余弦，只不过是借了它的名字，实际是借用了它的概念变成了是代数意义上的“夹角余弦”，用来衡量样本向量间的差异。
余弦夹角
Cosine相似度是根据两个向量的夹角计算相似度，夹角越小相似度越高。
夹角越小，余弦值越接近于1，反之则趋于-1。我们假设有x1与x2两个向量：
$\cos (\theta)=\frac{\sum_{k=1}^{n} x_{1 k} x_{2 k}}{\sqrt{\sum_{k=1}^{n} x_{1 k}^{2}} \sqrt{\sum_{k=1}^{n} x_{2 k}^{2}}}$
相似度计算公式为：
$\operatorname{sim}_{x, Y}=\frac{X Y}{\|X\| \cdot\|Y\|}=\frac{\sum_{i=1}^{n}\left(x_{i} * y_{i}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}\right)^{2}} \cdot \sqrt{\Sigma_{i=1}^{n}\left(y_{i}\right)^{2}}}$
改进公式考虑到了两个向量相同个体个数，X向量大小，Y向量大小，注意：
$\operatorname{sim}_{x, y} \neq \operatorname{sim}_{y, x}$

实现过程

以本数据库，教师研修学分档案为例，到了每年需要选择研修课程的时候，某教师不知道应该选什么课程适合自己，于是就询问身边的其他老师，看看有什么课程推荐，这时候大部分人都会倾向于问跟这位老师品味差不多的人。而这也就是协同过滤的核心思想。

一般来说，协同过滤推荐分为三种类型。第一种是基于教师(user-based)的协同过滤，第二种是基于项目(item-based)的协同过滤，第三种是基于模型(model based)的协同过滤。

由于基于模型的协同过滤比较有针对性，本节暂不使用，该案例从教师实际数据出发，分别使用UserCF和ItemCF两种相似度推荐算法来给教师推荐课程。

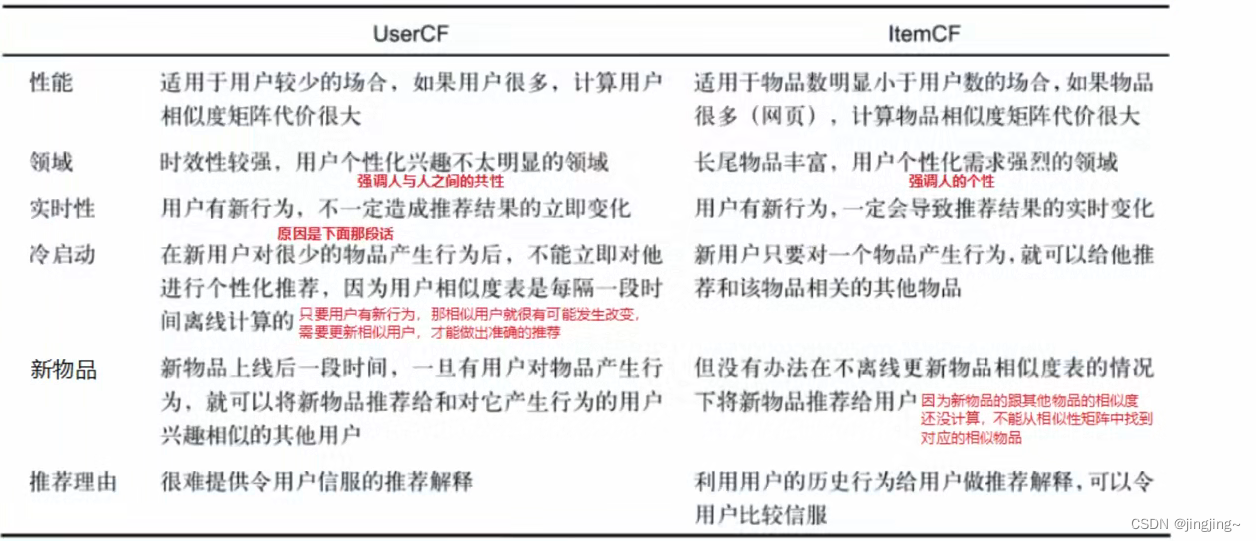
UserCF和ItemCF的比较

Item CF是利用课程间的相似性来推荐的，所以假如教师的数量远远超过课程的数量，那么可以考虑使用Item CF，比如购物网站，因其课程的数据相对稳定，因此计算课程的相似度时不但计算量较小，而且不必频繁更新;User CF更适合做新闻、博客或者微内容的推荐系统，因为其内容更新频率非常高，特别是在社交网络中，User CF是一个更好的选择，可以增加教师对推荐解释的信服程度。

基于教师(user-based)的协同过滤实现过程

基于教师的协同过滤的基本原理是，根据所有教师对课程或者信息的偏好，发现与当前教师口味和偏好相似的教师群，然后基于这些教师的历史偏好，为当前教师进行推荐。

具体过程：

计算就是将一个教师对所有课程的偏好作为一个向量来计算教师之间的相似度（找领居）
找到 K 邻居后，根据邻居的相似度权重以及他们对课程的偏好，（看邻居偏好）
预测当前教师没有偏好的未涉及课程，计算得到一个排序的课程列表作为推荐。（召回排序）

教师/课程	课程A	课程B	课程C	课程D
教师A	√		√	推荐
教师B		√
教师C	√		√	√

在这里插入图片描述
假设教师A喜欢课程A、课程C，教师B喜欢课程B，教师C喜欢课程A、课程C和课程D。从这些教师的历史偏好中，我们可以看出教师A和教师C的偏好是类似的。同时我们可以看到教师C喜欢课程D，所以我们可以猜想教师A可能也喜欢课程D，因此可以把课程D推荐给教师A。

基于课程(item-based)的协同过滤实现过程

基于课程的协同过滤推荐的基本原理也是类似的，只是它使用所有教师对课程或者信息的偏好，发现课程和课程之间的相似度，然后根据教师的历史偏好信息，将类似的课程推荐给当前教师。

具体过程：

从计算的角度看，就是将所有教师对某个课程的偏好作为一个向量来计算课程之间的相似度，（找教师偏好的“共性”课程）
得到课程的相似课程后，根据教师历史的偏好预测当前教师还没有表示偏好的课程，计算得到一个排序的课程列表作为推荐。（预测召回，排序）

教师/课程	课程A	课程B	课程C
教师A	√		√
教师B	√	√	√
教师C	√		推荐

在这里插入图片描述
假设教师A喜欢课程A、课程C，教师B喜欢课程A、课程B和课程C，教师C喜欢课程A。从这些教师的历史偏好中，我们可以分析出课程A和课程C是比较相似的，因此我们可以把课程C推荐给教师C。

案例实战

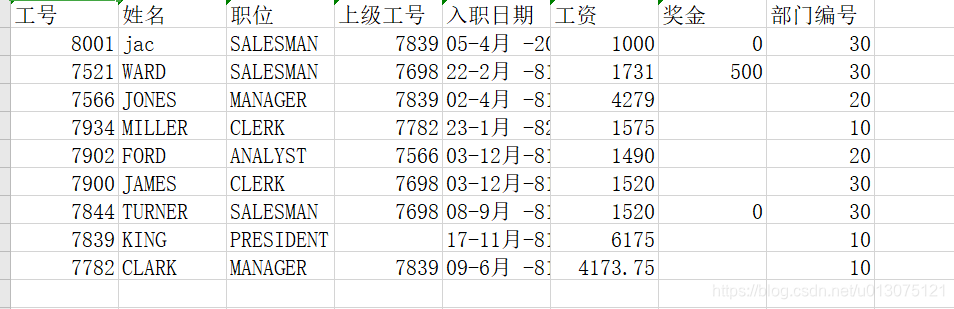
本案例提取了数据库中教师研修学分数据，根据教师历年选课的情况，给老师推荐课程。
数据库提取出来的数据如下图所示：
在这里插入图片描述
首先，导入数据

import numpy as np
import pandas as pd# 读取原始数据文件
# df = pd.read_excel('../原始数据/原始数据.xlsx')header = ['user_id', 'item_id', 'rating', 'timestamp']
df = pd.read_csv('../原始数据/原始数据 - 副本.csv', names=header)

然后对数据进行预处理，由于教师的进修编号，以及选择的课程，不是标准的数字化数据，无法直接带入矩阵进行行列运算，所以对进修编号，课程名称进行重新编码，方便以后矩阵的运算：

# 数据预处理
# 教师对所有课程只有选上1和未选0两种状态，顾选课为1
# 1.进修编号及课程按照从0开始重新编码，为了后续矩阵运算
user_list = pd.DataFrame({'进修编号': df.user_id.unique(), '矩阵编号': np.arange(df.user_id.unique().shape[0])})
items_list = pd.DataFrame({'课程名称': df.item_id.unique(), '矩阵编号': np.arange(df.item_id.unique().shape[0])})
user_list.to_excel('../输出数据/进修编号矩阵编码.xlsx', index=False)
items_list.to_excel('../输出数据/课程名称矩阵编码.xlsx', index=False)i = 0
for line in user_list.itertuples():     #.itertuples()可以使user_list分成多个对象df.loc[(df['user_id'] == line[1]), 'user_id'] = line[2]print('重新编码教师，已完成',round(i/user_list.shape[0]*100.00,2), '%', end="\r")i+=1i = 0
for line in items_list.itertuples():df.loc[(df['item_id'] == line[1]), 'item_id'] = line[2]print('重新编码课程，已完成',round(i/items_list.shape[0]*100.00,2), '%', end="\r")i+=1print(df)
df.to_excel('../输出数据/矩阵数据.xlsx', index=False)

预处理后的数据如下图所示：
在这里插入图片描述
然后，通过以下代码得出教师以及课程的总数：

# 数据计算
# 计算唯一教师和课程数量
n_users = df.user_id.unique().shape[0]
n_items = df.item_id.unique().shape[0]
print('Number of teachers = ' + str(n_users) + ' | Number of courses = ' + str(n_items))

输出结果如下：
在这里插入图片描述
接着我们使用scikit-learn库将数据集分割成测试和训练。train_test_split根据测试样本的比例（test_size），本例中是0.2，来将数据混洗并分割成两个数据集。然后开始基于内容协同过滤。第一步是创建uesr-item矩阵，此处需创建训练和测试两个UI矩阵。

# 使用scikit-learn库将数据集分割成测试和训练。train_test_split根据测试样本的比例（test_size）
# ，本例中是0.2，来将数据混洗并分割成两个数据集
from sklearn.model_selection import train_test_splittrain_data, test_data = train_test_split(df, test_size=0.2)# 基于内容的协同过滤
# 第一步是创建uesr-item矩阵，此处需创建训练和测试两个UI矩阵
# 初始化一个user行，items列
train_data_matrix = np.zeros((n_users, n_items))
for line in train_data.itertuples():train_data_matrix[line[1], line[2]] = line[3]# print(train_data_matrix)
# a = pd.DataFrame(train_data_matrix)
# # a.to_excel('../输出数据/test.xlsx', index=False)
# print(a)test_data_matrix = np.zeros((n_users, n_items))
for line in test_data.itertuples():test_data_matrix[line[1], line[2]] = line[3]

接下来通过 pairwise_distances求相似度:

# 计算相似度
# 使用sklearn的pairwise_distances函数来计算余弦相似性
from sklearn.metrics.pairwise import pairwise_distances
# 计算用户相似度
user_similarity = pairwise_distances(train_data_matrix, metric='cosine')
# 计算物品相似度
item_similarity = pairwise_distances(train_data_matrix.T, metric='cosine')

最后进行预测推荐：

# 预测
def predict(ratings, similarity, type='user'):# 基于用户相似度矩阵的if type == 'user':mean_user_rating = ratings.mean(axis=1)# You use np.newaxis so that mean_user_rating has same format as ratingsratings_diff = (ratings - mean_user_rating[:, np.newaxis])pred = mean_user_rating[:, np.newaxis] + similarity.dot(ratings_diff) / np.array([np.abs(similarity).sum(axis=1)]).T# 基于物品相似度矩阵elif type == 'item':pred = ratings.dot(similarity) / np.array([np.abs(similarity).sum(axis=1)])return pred# 预测结果
item_prediction = predict(train_data_matrix, item_similarity, type='item')
user_prediction = predict(train_data_matrix, user_similarity, type='user')user_list = pd.read_excel('../输出数据/进修编号矩阵编码.xlsx', index=False)
items_list = pd.read_excel('../输出数据/课程名称矩阵编码.xlsx', index=False)
user = user_list.进修编号.array     #提取教师原始编号
items = items_list.课程名称.array   #提取课程原始编号item_prediction = pd.DataFrame(item_prediction, index=user, columns=items)
item_prediction_forty = item_prediction[0:40]user_prediction = pd.DataFrame(user_prediction, index=user, columns=items)
user_prediction_forty = user_prediction[0:40]user_prediction_forty.to_excel('../输出数据/基于用户预测结果40.xlsx')
item_prediction_forty.to_excel('../输出数据/基于课程预测结果40.xlsx')