关系代数及其运算符

关系代数是一种抽象的查询语言，通过关系的运算来表达查询
关系代数常使用的运算符由如下几类

• 集合运算符：∪（并）、∩（交）、-（差）、×（笛卡尔积）
• 专门的关系运算符：σ（选取）、∏（投影）、∞（连接）、*（自然连接）、÷（除）
• 算术比较符：>、≥、＜、≤、=、≠
• 逻辑运算符：∧（与）、∨（或）、¬（非）

其中算数比较符的使用就不多说，组要对集合运算符和关系运算符进行学习
需要注意的是，∩与∧两中运算符，前者是针对集合的，后者是针对元素的

集合运算符

前提
关系R、S需要满足相容

1. 具有相同的度n
2. 相同的属性需要来自同一个域（可以说是R、S具有相同的属性集U）

给出如下两个表

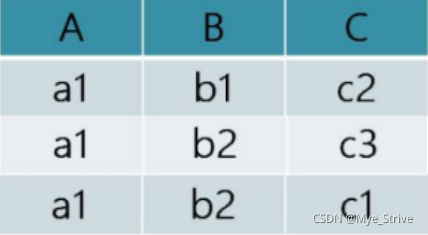
R

A	B	C
a1	b1	c1
a1	b1	c2
a2	b2	c1

S

A	B	C
a1	b1	c1
a2	b2	c1
a2	b3	c2

1. 交（∩）
   R∩S = {t | t∈R ∧ t∈S}，（t是一个元组）那么得到的结果如下

A	B	C
a1	b1	c1
a2	b2	c1

2. 并（∪）
   R∪S = {t | t∈R ∨ t∈S}，结果如下

A	B	C
a1	b1	c1
a2	b2	c1
a1	b1	c2
a2	b3	c2

3. 差（-）
   R-S = {t | t∈R ∧ ¬t∈S}，结果如下

A	B	C
a1	b1	c2

R-S就是，在R中取出与S相同的元组

4. 广义笛卡尔积（×）
   R×S = {t_r ⌒t_s| t_r∈R ∧ t_s∈S}，结果如下

Ar	Br	Cr	As	Bs	Cs
a1	b1	c1	a1	b1	c1
a1	b1	c1	a2	b2	c1
a1	b1	c1	a2	b3	c2
a1	b1	c2	a1	b1	c1
a1	b1	c2	a2	b2	c1
a1	b1	c2	a2	b3	c2
a2	b2	c1	a1	b1	c1
a2	b2	c1	a2	b2	c1
a2	b2	c1	a2	b3	c2

为什么说是广义笛卡尔积呢？
应为在前面的笛卡尔积中，是只有单一数据的值域之间进行的计算，而这里是通过连接符⌒，来得到两个关系元组的组合
由此能够发现，对于广义笛卡尔积，不需要两个关系满足相容

关系运算符

在此之前需要先了解几个东西

1. 设关系模式为R(A₁,A₂,A₃,…,A_n)，它的一个关系为r，t是r的一个元组，t∈R，t[Ai]表示t中的一个分量
2. A={A₁,A₂,…,A_k}, ~ A={A_k+1,A_k+2,…,A_n},A（还有~ A）称为属性列或域列，t[A]={t[A₁],t[A₂],…,t[A_k]} 表示元组t在A上的分量集合（A+~A=R）
3. R、S分别为n、m目关系，t_r∈R，t_s∈S，t_r⌒t_s 称为元组的连接，连接后的得到的是m + n列的元组
4. 给定关系R(X,Z),X和Z为两个属性组（X、Z可能代表多个属性，也就是将U分为X、Z两部分），当t[X]=x时，x在R中的象集为Z_x={t[Z] | t∈R，t[X]=x},它表示R中的属性组X上，值为x的元组集合在Z上的分量集合，这个集合称为象集（就是在t中t[X]=x部分的t[Z]的集合称为x在R中的象集）

上面的前三个都很好理解，最后一个象集看着比较绕口
用人话来说就是将关系R的属性集U分为两个部分X和Z，x与z是X和Z的某一个值
因此有：t = t[X] + t[Z]
在R中R的元组中找到符合t[X] = x的元组t（也许会找到多个，也许没有）
则t[Z] = t - t[X]就是x在R中的象集
例子，用前面的R表
X代表A，Z代表B和C，那么x=a1时，象集为
{（b1，c1），（b1，c2）}

前面的几样弄清楚后，关系运算符理解起来就很简单了

1. 选取(σ)
   σ_F ( R ) = {t | t ∈ R ∧ F(t) = ‘真’}

σ是运算符，F是规定的选取条件，F(t) = '真’表示元组t满足条件
条件是根据需要自定义的
所以，选取的含义就是：选取满足条件的元组
比如：σ_A=a1 ( R )，表示在R中寻找A=a1的元组，结合之前的R的表，答案为前两行

2. 投影(∏)
   ∏_A( R ) = {t[A] | t ∈ R}

∏是运算符，A是一个属性列
含义是：列出R中属性列A的分量集合（得到的数据是不重复的，重复部分会删除的）
例子：∏_A( R ) = {a1, a2}

3. 连接(⌒)
   

∞与⌒都是连接运算符，只不过一个连接关系，一个连接元组
θ是比较运算符，可以是大于，小于等
X是R的属性列，Y是S的属性列，X、Y需要来自同一个域
含义：将R与S中符合条件的元组连接起来
还可写作σ_XθY( R×S )

• 等值连接：当θ为=时，得到的就是等值连接
• 自然连接：R*S = {t_r⌒t_s | t_r∈R∧t_s∈S∧t_r[Y] = t_s[Y]}
  当R与S中属性列X和Y相同的时候（属性名需要相同，且来自同一个域），将等值连接后重复部分去掉得到的就是自然连接
  下面两个表分别是等值和自然连接（条件是R.B = S.B，也假设B是相同名的）

Ar	B	Cr	As	B	Cs
a1	b1	c1	a1	b1	c1
a1	b1	c2	a1	b1	c1
a2	b2	c1	a2	b2	c1

Ar	B	Cr	As	Cs
a1	b1	c1	a1	c1
a1	b1	c2	a1	c1
a2	b2	c1	a2	c1

4. 除(÷)
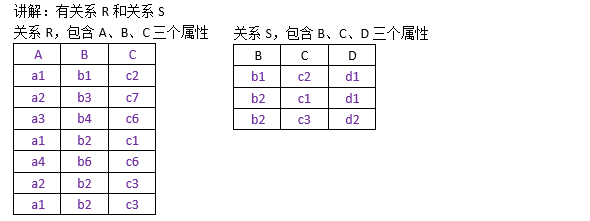
   给定关系R(X,Y)和S(Y,Z),其中X,Y,Z为属性组，R中的Y与S中的Y可以有不同的属性名，但必须来自相同的域
   P(X)=R÷S，为R与S的除运算（得到的是X的属性列上的投影）
   其中R÷S = {t_r[X] | t_r∈R∧∏_Y(S)∈Y_x}

Y_x是x在R中的象集
这个是这样的，假设t[X]的取值范围为{x₁,x₂,…,x_n}
则当t[X]=x₁时，计算此时的X在R中的象集（得到关于t[Y]的集合），判断S中，属性列Y的分量集合是否是该象集的子集，若是，这个t[X]就进入除法计算结果中，以此类推，计算t[X]=x₂，····类推得到最后结果。

下面给个课本上的例子
R

A	B	C	D
a1	b2	c3	d5
a1	b2	c4	d6
a2	b4	c1	d3
a3	b5	c2	d8

S

C	D	E
c3	d5	f3
c4	d6	f4

R（X，Y）,S(Y，Z)
X代表A、B，Y代表C、D，Z代表E
t_Y[S] = {（c3，b5），（c4，b6）}
步骤如下

• t[X] = (a1，b1)时，Y_x = {（c3，b5），（c4，b6）}
  t_Y[S]∈Y_x成立，（a1，b1）进入运算结果
• t[X] = (a2，b4)时，Y_x = {（c1，d3）}
  t_Y[S]∈Y_x不成立
• t[X] = (a3，b5)时，Y_x = {（c2，d8）}
  t_Y[S]∈Y_x不成立

所以最后的结果为

A	B
a1	b2

总结

元组、分量需要分清楚
集合运算和关系运算的最主要区别是关系是否需要相容