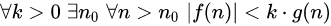做软考习题时，碰到了这样的一道题：

关于算法复杂度渐进符号（O、Ω、θ），详细解释可参考：
【双语字幕】什么是算法复杂度渐进符号？阿布老师算法课11

这里节选总结了视频的重点内容，并补充了视频中缺失的部分细节、以及我的个人理解：

==================================================

（1）常见函数阶数由低到高排列：

请记住它！

（2）O（Big-Oh，大O表示法）——表示上限

构造形如f(n) = c * g(n)形式的不等式，使得在n ≥ n₀的条件下，满足0 ≤ f(n) ≤ c * g(n)。（n₀是自己取的一个数）

eg：
如图，待分析式f（n）=2n+3
此时，可以构造式子2n+3n，可以保证当n≥1时，f（n）= 2n+3 ≤ 2n+3n = 5n成立
此时，c*g（n）= 5n（c为系数5，g（n）=n）
因为g（n）= n，所以f（n）=O(n)

ps：大O表示法可以用比最接近的函数阶数更大的函数来表示。

向上面这种f（n）= 2n+3 ≤ 2n+3n = 5n的情况：用O(n)是最贴切的情况，但是也可以用O(n^2）、O(nlogn)等阶数更高的形式进行表达，只是阶数过大的时候也没什么意义了。

（3）Omega（Ω）——表示下限

构造形如f(n) = c * g(n)形式的不等式，使得在n ≥ n₀的条件下，满足f(n) ≥ c * g(n) ≥ 0。（n₀是自己取的一个数）

eg：
如图，待分析式f（n）=2n+3
此时，可以构造式子2n+3n，可以保证当n≥1时，f（n）= 2n+3 ≥ 1 * logn成立
此时，c*g（n）= 1 * logn（c为系数1，g（n）=logn）
因为g（n）= logn，所以f（n）=O(logn)

ps：Omega（Ω）表示法可以用比最接近的函数阶数更大的函数来表示。

同理，向上面这种f（n）= 2n+3 ≥ 1 * logn的情况：用O(logn)是最贴切的情况，但是也可以用O（1）这样阶数更低的形式进行表达，只是阶数过低的时候也没什么意义了。

（4）Theta（θ）——平均界限

相比大O和Ω，平均界限θ的选取往往比较严格，只会有一种。

eg.
如图，待分析式f（n）=2n+3
此时，可以构造式子c1 * g(n) = 1 * n和式子c2 * g(n) = 5 * n，可以保证当n≥1时，n ≤ f（n）= 2n+3 ≤ 5n成立。

此时，不等式两边的g（n）均为n，此时g(n) = n就是平均界限θ。

ps：
平均界限要求不等式两边的g（n）必须相同，如上面的例子，不能左边的g（n）是n，右边的g（n）取n²。

=================================================
所以，再看一下这道软考题：

A：取f（n）=n²
当n≥1时，1/2 * n² ≤ n²≤ 2n²，所以f（n）= θ（n²），A正确

B：取f（n）=n²
当n≥1时，n²≤ 2n²，所以f（n）=O（n²），B正确

C：
找不到一个n₀，使得在n ≥ n₀的条件下，满足0 ≤ f(n)=n² ≤ c * g(n) = c* n，C错误

D：取f（n）=n²
当n≥1时， n² ≤ n³，所以f（n²）= O（n³），A正确

===================================================
ps：
大O并不是只能表示最坏情况，Ω不是只能表示最好情况，其实用任何符号都可以表示最好情况/最坏情况。
请不要弄混淆。