感谢作者分享,原文链接:http://blog.csdn.net/u012816041/article/details/49888631
大O,渐进表示法,接下来我尝试用最简单的方式进行说明。
学习算法我经常听到这个词汇,我一开始很难理解,什么鬼?其实简单的说,就是描述一个算法的好坏词。
大O,可以认为它的含义是“order of”(大约是)。
简单列举几个,当人们形容:
某个算法的时间复杂度是O(1),就说明这是一个优秀的算法。
某个算法的时间复杂度是O(logn),就说明这是一个良好的算法。
某个算法的时间复杂度是O(n),就说明这个算法还不错。
某个算法的时间复杂度是O(n2),就说明这个算法差一些了。
上面那些记住后,至少让你,听到这个词后不会呆。。额。。
其实知其然不知其所以然是很可怕的,不过上面内容,起码保证了过一段时间不会一无所知。接下来是具体的数学分析和其他的一些表示法,直接上维基百科了。
大O符号
注:“order”在全文中被译为“阶”,也可以另译为“数量级”。
大O符号(英语:Big O notation)是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。
大O符号是由德国数论学家保罗·巴赫曼(Paul Bachmann)在其1892年的著作《解析数论》(Analytische Zahlentheorie)首先引入的。而这个记号则是在另一位德国数论学家艾德蒙·朗道(Edmund Landau)的著作中才推广的,因此它有时又称为朗道符号(Landau symbols)。代表“order of ...”(……阶)的大O,最初是一个大写的希腊字母'Ο'(omicron),现今用的是大写拉丁字母‘O’,但从来不是阿拉伯数字‘0’。
使用
这个符号有两种形式上很接近但迥然不同的使用方法:无穷大渐近与无穷小渐近。然而这个区别只是在运用中的而不是原则上的——除了对函数自变量的一些不同的限定, “大O”的形式定义在两种情况下都是相同的。[来源请求]
无穷大渐近
大O符号在分析算法效率的时候非常有用。举个例子,解决一个规模为 的问题所花费的时间(或者所需步骤的数目)可以表示为:
的问题所花费的时间(或者所需步骤的数目)可以表示为: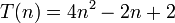 。当
。当 增大时,
增大时, 项将开始占主导地位,而其他各项可以被忽略。 举例说明:当
项将开始占主导地位,而其他各项可以被忽略。 举例说明:当 ,
, 项是
项是  项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。
项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。
进一步看,如果我们与任一其他级的表达式比较, 项的系数也是无关紧要的。例如:一个包含
项的系数也是无关紧要的。例如:一个包含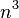 或
或 项的表达式,即使
项的表达式,即使 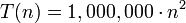 ,假定
,假定  ,一旦
,一旦 增长到大于1,000,000,后者就会一直超越前者(
增长到大于1,000,000,后者就会一直超越前者( )。
)。
这样,大O符号就记下剩余的部分,写作:
或
并且我们就说该算法具有 阶(平方阶)的时间复杂度。
阶(平方阶)的时间复杂度。
无穷小渐近
大O也可以用来描述数学函数估计中的误差项。例如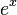 的泰勒展开:
的泰勒展开:
-
 当
当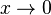 时
时
这表示,如果 足够接近于0,那么误差
足够接近于0,那么误差 的绝对值小于
的绝对值小于 的某一常数倍。
的某一常数倍。
形式化定义
给定两正值函数 和
和 ,定义:
,定义:
-
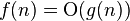 ,条件为:存在正实数
,条件为:存在正实数 和
和 ,使得对于所有的
,使得对于所有的 ,有
,有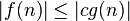
上述的定义表明,当 足够大,大过一个特定的
足够大,大过一个特定的 时,且存在一个正数
时,且存在一个正数 ,使得
,使得 不大于
不大于 ,则
,则 是
是 的
的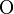 表示。
表示。 和
和 的关系可以理解为
的关系可以理解为 是
是 的一个上界,也可以理解为
的一个上界,也可以理解为 最终至多增涨的速度与
最终至多增涨的速度与 一样快,但不会超过
一样快,但不会超过 的增涨速度。
的增涨速度。
常用的函数阶
下面是在分析算法的时候常见的函数分类列表。所有这些函数都处于 趋近于无穷大的情况下,增长得慢的函数列在上面。
趋近于无穷大的情况下,增长得慢的函数列在上面。 是一个任意常数。
是一个任意常数。
| 符号 | 名称 |
|---|---|
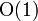 | 常数(阶,下同) |
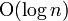 | 对数 |
![\Omicron[(\log n)^c]\!](https://upload.wikimedia.org/math/a/1/2/a1290e02605a773cc41b2583baa2c678.png) | 多对数 |
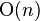 | 线性,次线性 |
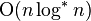 |  为迭代对数 为迭代对数 |
 | 线性对数,或对数线性、拟线性、超线性 |
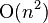 | 平方 |
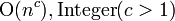 | 多项式,有时叫作“代数”(阶) |
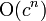 | 指数,有时叫作“几何”(阶) |
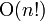 | 阶乘,有时叫做“组合”(阶) |
一些相关的渐近符号
大O是最经常使用的比较函数的渐近符号。
| 符号 | 定义 |
|---|---|
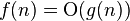 | 渐近上限 |
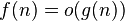 | asymptotically negligible(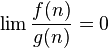 ) ) |
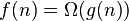 | 渐近下限 (当且仅当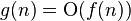 ) ) |
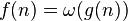 | asymptotically dominant(当且仅当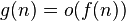 ) ) |
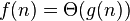 | asymptotically tight bound(当且仅当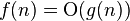 且 且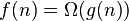 ) ) |
注意
大O符号经常被误用:有的作者可能会使用大O符号表达大Θ符号的含义。因此在看到大O符号时应首先确定其是否为误用。
大Ω符号
大Θ符号
大Θ符号是大O符号和大Ω符号的结合。即:![f(\nu)=\Theta[g(\nu)]\!](https://upload.wikimedia.org/math/1/d/a/1da7e4f02404c76e695f91a3dbe4fb19.png) 若
若![\begin{cases}f(\nu)=\Omicron[g(\nu)]\\f(\nu)=\Omega[g(\nu)]\end{cases}](https://upload.wikimedia.org/math/4/f/5/4f51d129e7dd76e7c678c9888606f13a.png) 。
。
这一符号首先由高德纳于1970年提出[1]。
注意
大Θ符号经常被误用;有的作者可能会使用大O符号表达大Θ符号的含义。因此在看到大O符号时应首先确定其是否为误用。
我发现读完维基百科还是有一些不清晰的地方,或者不好理解的地方,再加上这些。
设函数f ( n )代表某一算法在输入大小为n的情况下的工作量(效率),则在n趋向很大的时候,我们将f (n)与另一行为已知的函数g(n)进行比较:
1)如果 0,则称f (n)在数量级上严格小于g(n),记为f (n)=o( g(n))。
0,则称f (n)在数量级上严格小于g(n),记为f (n)=o( g(n))。
2)如果
 ,则称f (n)在数量级上严格大于g(n),记为f (n)=w( g(n))。
,则称f (n)在数量级上严格大于g(n),记为f (n)=w( g(n))。
3)如果 c,这里c为非0常数,则称f (n)在数量级上等于g(n),即f (n)和g(n)是同一个数量级的函数,记为:f (n)=Θ( g(n))。
c,这里c为非0常数,则称f (n)在数量级上等于g(n),即f (n)和g(n)是同一个数量级的函数,记为:f (n)=Θ( g(n))。
4)如果f (n)在数量级上小于或等于g(n),则记为f (n)=O( g(n))。
5)如果f(n)在数量级上大于或等于g(n),则记为f (n)=Ω( g(n))。
这里我们假定f (n),g (n)是非负单调的,且极限存在。如果这个极限 不存在,则无法对f (n)和g (n)进行比较。在进行此种计算时,一个经常用到的技术是洛必达(L'Hopital)法则。该法则由17世纪法国数学家Guillaume de L'Hopital发现(也有人认为是瑞士数学家Johann Bernoulli发现的)。该法则声称,两个函数的比率极限等于两个函数的导数的比率极限,这里当然假定两个函数的导数比率的极限存在,即有:
不存在,则无法对f (n)和g (n)进行比较。在进行此种计算时,一个经常用到的技术是洛必达(L'Hopital)法则。该法则由17世纪法国数学家Guillaume de L'Hopital发现(也有人认为是瑞士数学家Johann Bernoulli发现的)。该法则声称,两个函数的比率极限等于两个函数的导数的比率极限,这里当然假定两个函数的导数比率的极限存在,即有:

有了这个定义,就可以对素性测试的两个算法进行比较了。


![f(\nu)=\Omega[g(\nu)]](https://upload.wikimedia.org/math/4/8/2/482df7fab83bf7b2bd20726a40fce736.png) 若存在
若存在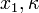 使得:
使得: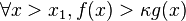 .
.![\begin{cases}f(\nu)=\Omicron[g(\nu)]\\g(\nu)=\Omega[f(\nu)]\end{cases}](https://upload.wikimedia.org/math/2/a/b/2ab4ac0ff32eca3ead6ec6fca3278063.png) 。
。