复习排序算法
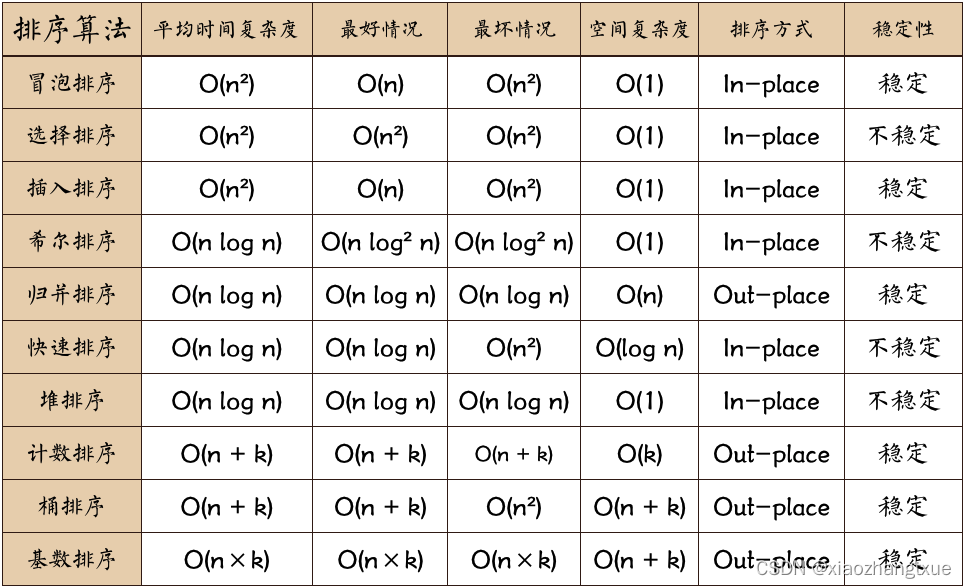
时间复杂度、空间复杂度、稳定新
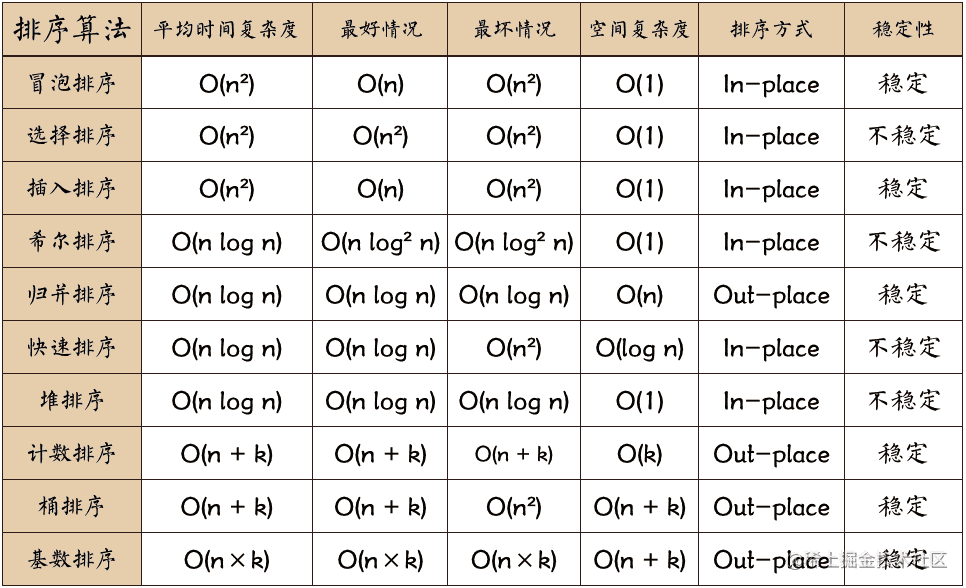
| 排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡 | O(n^2) | O(1) | 是 |
| 选择 | O(n^2) | O(1) | 不是 |
| 插入 | O(n^2) | O(1) | 是 |
| 希尔 | O(nlogn) | O(1) | 不是 |
| 快速 | O(nlogn) | O(nlogn) | 不是 |
1. 冒泡排序
-
思路:每一轮都对相邻的两个元素进行比较,如果逆序则交换位置,直到所有元素都排好序为止
-
基本操作:
-
代码:
ArrayList.prototype.bubbleSort = () => {const len = this.data.lengthfor (let i = 0; i < len - 1; i++) {for (let j = 0; j < len - 1 - i; j++) {if (this.data[j] > this.data[j + 1]) {const temp = this.data[j]this.data[j] = this.data[j + 1]this.data[j + 1] = temp}}}}
2. 选择排序
-
思路:每一轮都在待排序的元素中找出最大或最小的值,然后与此次待排序的元素中的第一个进行比较,如果逆序则交换位置;
-
基本操作:

-
代码:
ArrayList.prototype.selectSort = () => {/*** 以从小到大为例* 每一轮都从未排序元素中(不包括第一个)找到最小值与未排序元素的第一个元素进行比较* 符合条件则交换*/const len = this.data.lengthlet min = 0 // 记录最小值的索引for (let i = 0; i < len - 1; i++) {for (let j = i + 1; j < len; j++) {if (this.data[j] < this.data[min]) {min = j}}// 交换const temp = this.data[min]this.data[min] = this.data[i]this.data[i] = temp}}
3. 插入排序
-
思路:数组可以分为局部有序、局部无序两个部分,每一次都是将一个局部无序的元素按照其大小插入到局部有序序列当中,直到局部无序的元素全部插入为止
-
基本操作:
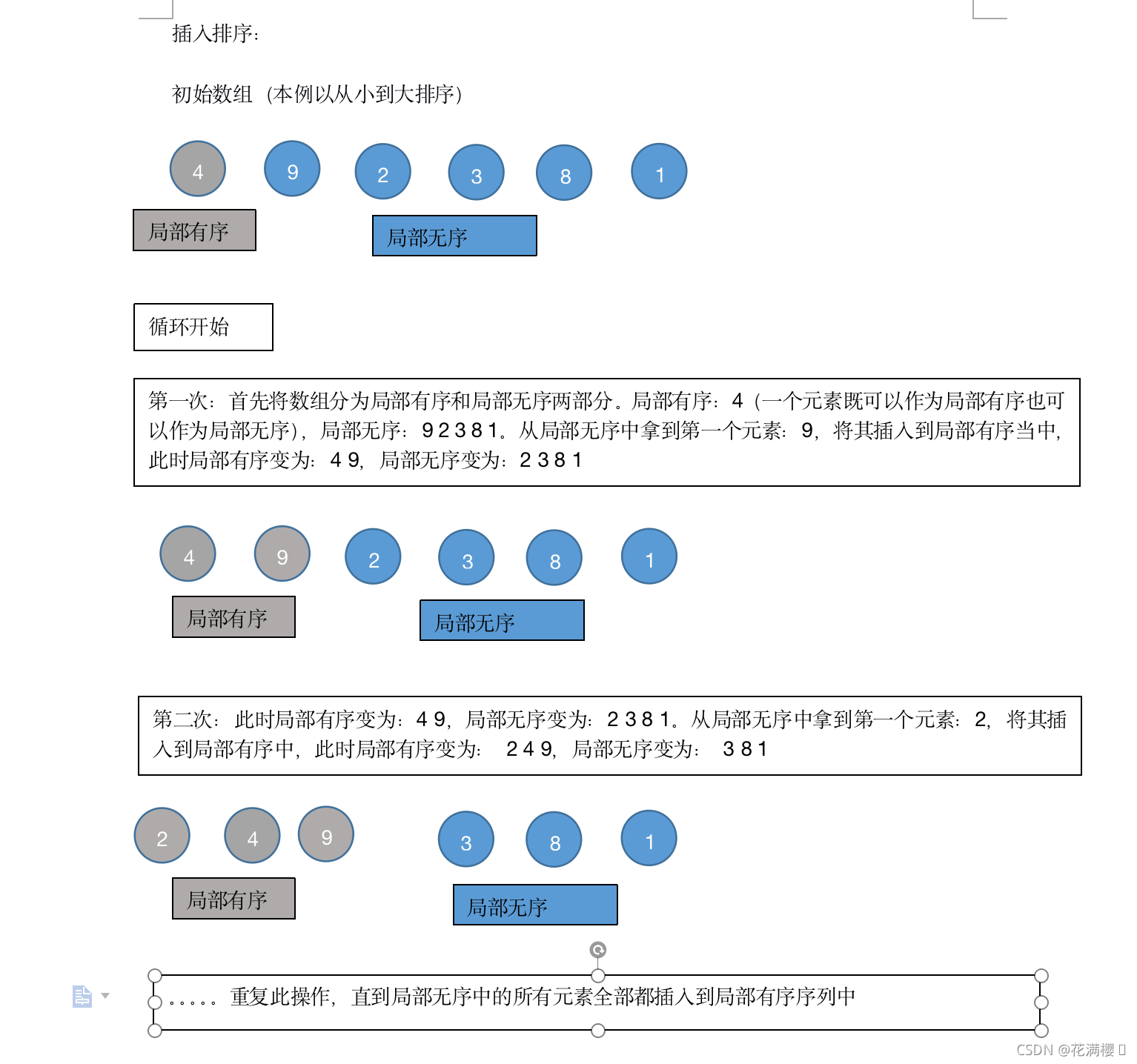
-
代码:
ArrayList.prototype.insertSort = () => {const len = this.data.length// 从第二个元素开始,因为默认以数组第一个元素作为局部有序的一个数列for (let i = 1; i < len; i++) {// 局部排序后面的第一个元素const temp = this.data[i]let j = i// 将 temp 这个元素与局部排序的数列进行比较,然后插入到正确的位置while (j > 0 && this.data[j - 1] > temp) {this.data[j] = this.data[j - 1]j--}this.data[j] = temp// 也可以使用二分法// 使用二分查找法找到需要插入元素的索引号// let r = i - 1// let l = 0// while (l <= r) {// const middle = Math.floor((l + r) / 2)// const value = this.data[middle]// if (value < temp) {// l = middle + 1// } else {// r = middle - 1// }// }// for (let k = i; k >= l; k--) {// this.data[k] = this.data[k - 1]// }// this.data[l] = temp}}
4.希尔排序
-
思路:在直接插入排序方法上改进:引入一个间隔增量(递减,这个增量每次循环都会递减,最小是1)将整个待排序列分割成多个子序列,对每一个子序列都进行直接插入排序,待整个序列基本有序的时候(即间隔增量 === 1),最后对全体元素再进行一次直接插入排序;间隔增量的作用就是将整个序列分割成多个子序列,对每个子序列进行插入排序,这样我们就可以将较小的元素用更少的比较次数就能找到其正确位置
-
基本操作:

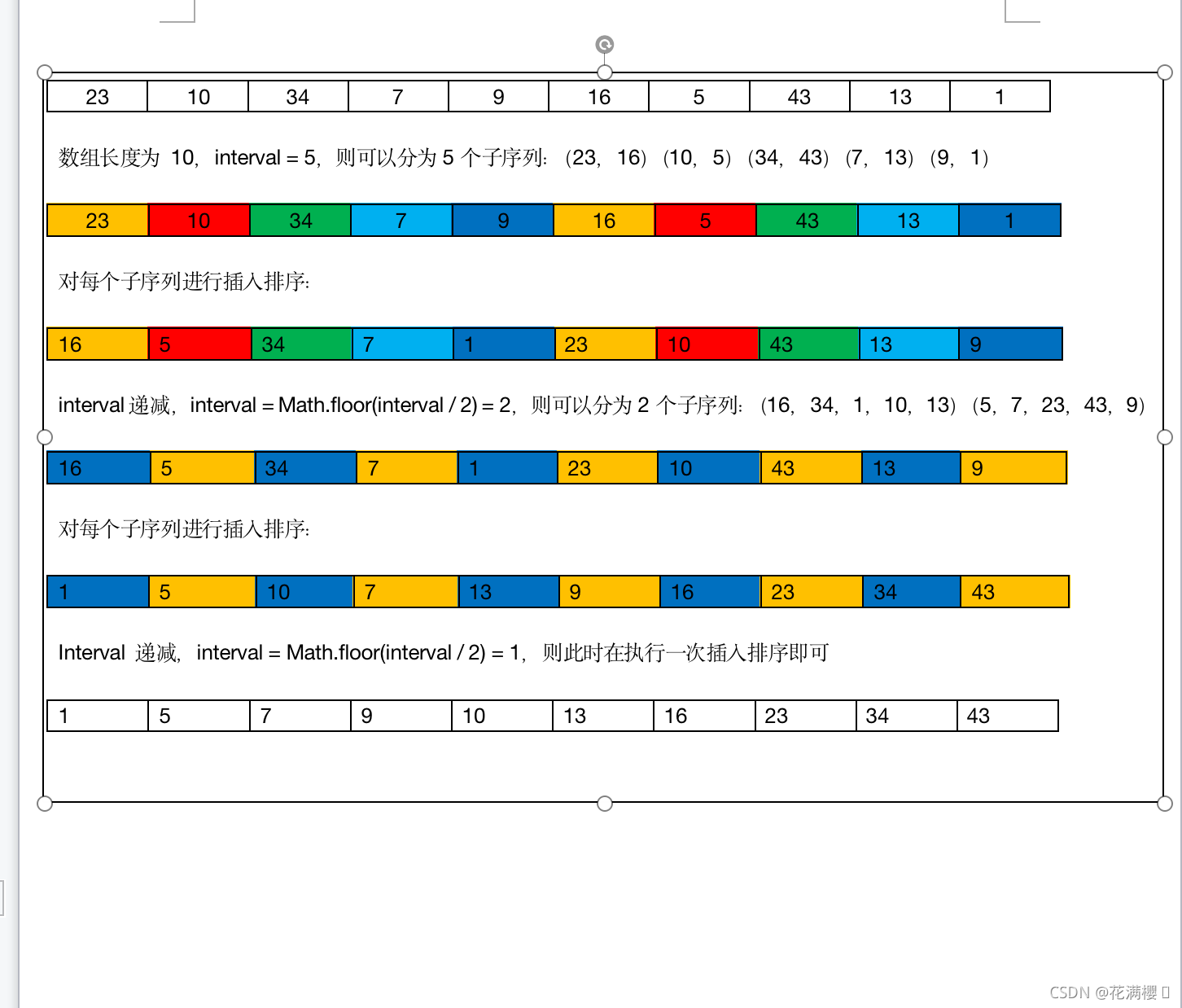
-
代码:
ArrayList.prototype.shellSort = () => {const len = this.data.length// 1. 获取增量let interval = Math.floor(len / 2)// 2. 增量递减while (interval >= 1) {// 3. 使用增量进行分组,开始遍历,执行插入排序// 此时由于引入了增量进行了分组,需要对插入排序进行改造for (let i = interval; i < len; i++) {// 4. 拿到当前元素,去与局部有序的元素进行比较,如果小于局部有序的元素就插入进去,(本例是从小到大排序)const temp = this.data[i]// 5. 记录当前元素的索引号,用于下一个 while 循环(与局部有序的元素进行比较的while循环)let j = i// 6. 当前元素与局部有序元素比较while (temp < this.data[j - interval] && (j - interval) >= 0) {this.data[j] = this.data[j - interval]j -= interval}// 7. 将当前元素插入进去this.data[j] = temp}interval = Math.floor(interval / 2)}
}
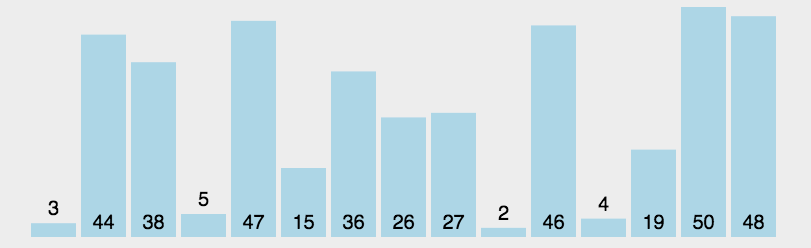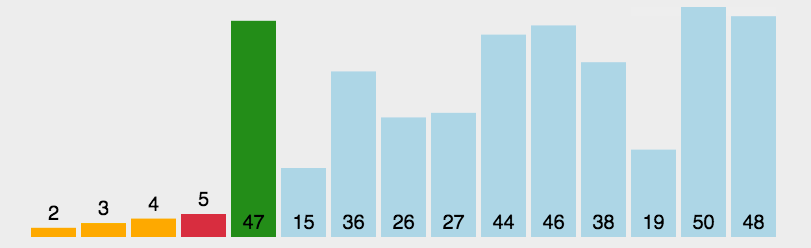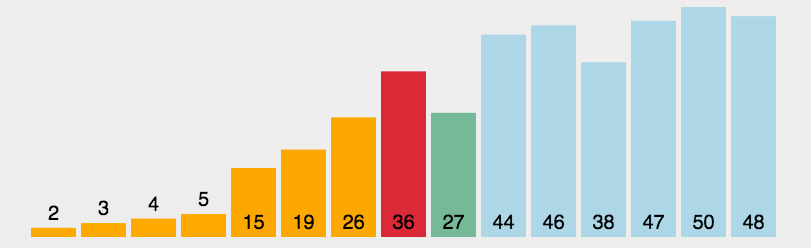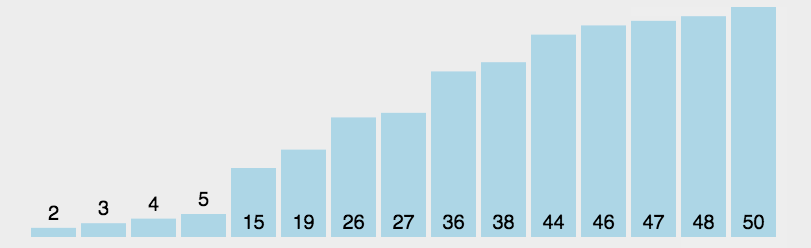
5.快速排序
- 思路:首先取一个元素(一般取数组的第一个元素,或者是挑选数组的第一个元素、中间元素、最后一个元素三个数的中位数)作为 中心;将所有比中心小的元素全部放到中心的左边位置,比中心大的元素全部放到中心的右边位置,以中心元素为界就形成了 两个子序列,然后对每个子序列重新选择中心元素并按照以上规则执行,直到每个子序列的元素只剩下一个
- 基本操作:

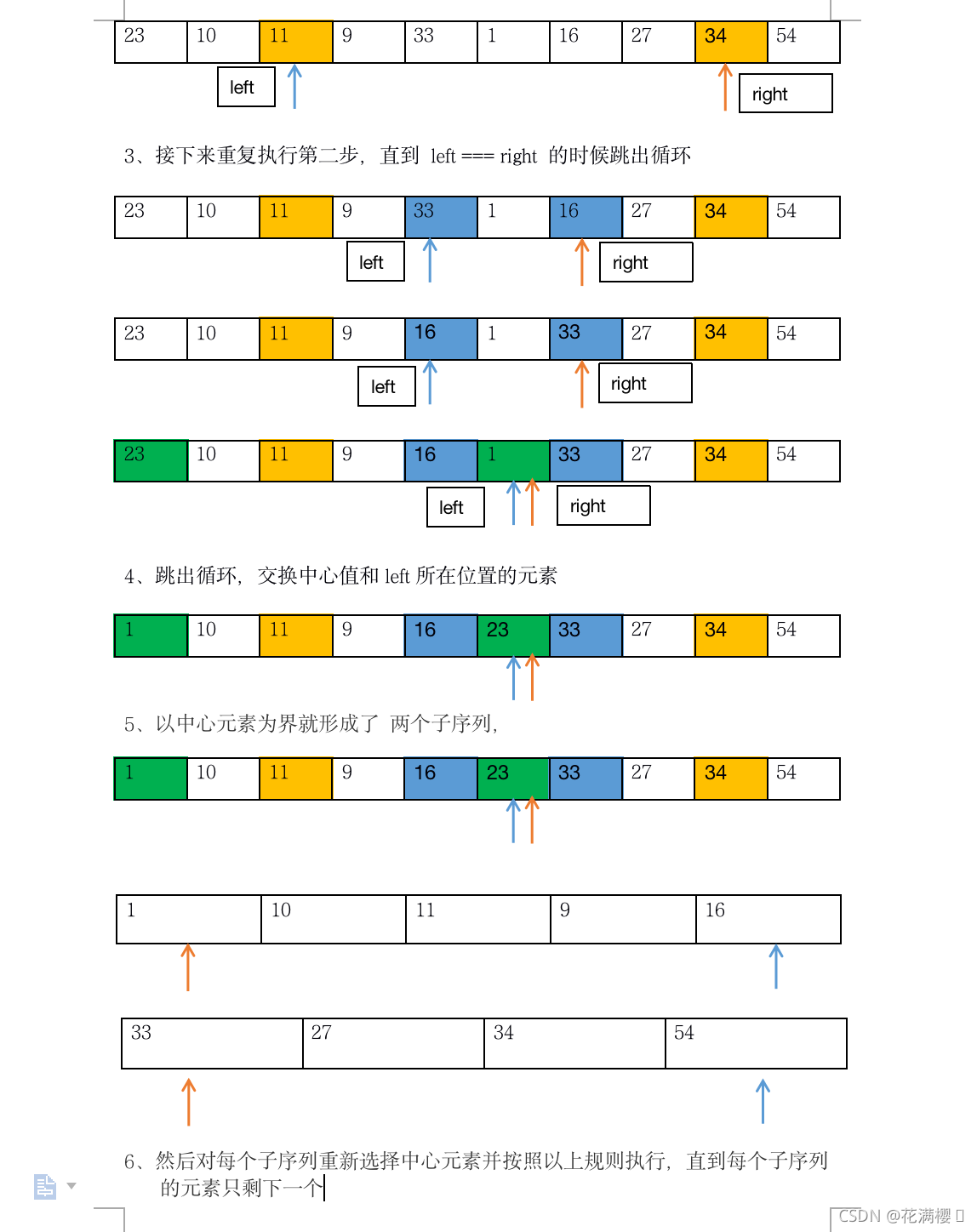
- 代码:
ArrayList.prototype.quickSort = () => {const quickSort = (data, left, right) => {// 0. 终止函数执行if (left >= right) return// 1. l,r 为此次排序 子序列的 索引号:l~rlet l = left, r = right// 2. 将第一个元素作为基值(中心值)const ele = data[l]// 3. 循环开始while (l < r) {// 4. 查询是否有小于基值的,获取小于基值的元素的索引号while (data[r] > ele && r > l) { // r > l 这个条件不能少,因为这个while循环会发生 r < l的情况r--}// 5. 查询是否有大于基值的,获取大于基值的元素的索引号while (data[l] <= ele && r > l) { // r > l 这个条件不能少,因为这个while循环会发生 r < l的情况l++}// 6. 跳出两个 while 循环,说明left right 停止移动了,左边遇到大于基值的,右边遇到小于基值的// 交换这两个元素的位置const temp = data[l]data[l] = data[r]data[r] = temp}// 7. 跳出最外层 while 循环,说明 这个基值已经找到了在数组中正确的位置了 将基值放到正确的位置data[left] = data[l] // 这里要使用left,因为left才是第一个值,经历过while循环后l,r已经变化了,此时 l === rdata[l] = ele// 8. 将基值左右两边的数组序列进行快速排序quickSort(data, left, l - 1)quickSort(data, l + 1, right)}quickSort(this.data, 0, this.data.length - 1)}
ArrayList结构的完整代码
function ArrayList() {this.data = []ArrayList.prototype.insert = (ele) => {this.data.push(ele)}ArrayList.prototype.toString = () => {console.log(this.data.join(' '))return this.data.join(' ')}// 冒泡排序ArrayList.prototype.bubbleSort = () => {/*** 对未排序的各个元素从头到尾依次比较相邻元素的大小关系,符合条件则交换位置,* 外层循环每一次都能找到一个最大值,排放到后面(从小到大)* 以此往复,直到排序已完成*/const len = this.data.lengthfor (let i = 0; i < len - 1; i++) {for (let j = 0; j < len - 1 - i; j++) {if (this.data[j] > this.data[j + 1]) {const temp = this.data[j]this.data[j] = this.data[j + 1]this.data[j + 1] = temp}}}}// 选择排序/*** 基本思想:* 在待排序的元素中找到最大或最小的,放到数组的最前面*/ArrayList.prototype.selectSort = () => {/*** 以从小到大为例* 每一轮都从未排序元素中(不包括第一个)找到最小值与未排序元素的第一个元素进行比较* 符合条件则交换* 相对于冒泡排序,交换次数耗时:O(n)*/const len = this.data.lengthlet min = 0 // 记录最小值的索引for (let i = 0; i < len - 1; i++) {for (let j = i + 1; j < len; j++) {if (this.data[j] < this.data[min]) {min = j}}// 交换const temp = this.data[min]this.data[min] = this.data[i]this.data[i] = temp}}// 插入排序(从小到大)(*)/*** 基本思想:* 每一步将一个待排序的元素,按照其元素大小插入到前面已经排序好的一组元素中,直到元素全部插入为止* 或* 数组可以分为两部分,局部有序,局部无序,每一步将一个局部无序的元素按照其值大小插入到局部有序当中,直到全部元素插入为止*/ArrayList.prototype.insertSort = () => {const len = this.data.length// 从第二个元素开始,因为默认一数组第一个元素作为局部排序的一个数列for (let i = 1; i < len; i++) {// 局部排序后面的第一个元素const temp = this.data[i]// // 将 temp 这个元素与局部排序的数列进行比较,// let j = i// while (j > 0 && this.data[j - 1] > temp) {// this.data[j] = this.data[j - 1]// j--// }// this.data[j] = temp// 改进:使用 二分查找法// 二分查找法let r = i - 1let l = 0while (l <= r) {const middle = Math.floor((l + r) / 2)const value = this.data[middle]if (value < temp) {l = middle + 1} else {r = middle - 1}}for (let k = i; k >= l; k--) {this.data[k] = this.data[k - 1]}this.data[l] = temp}}// 希尔排序(**)对插入排序的改进/*** 基本思想:* 引入一个间隔增量(递减),将整个待排序列分割成若干个子序列,分别对每一个进行直接插入排序,* 待整个序列 '基本有序' 的时候(即间隔增量 === 1),最后对全体元素再进行一次直接插入排序*/ArrayList.prototype.shellSort = () => {const len = this.data.length// 1. 获取增量let interval = Math.floor(len / 2)// 2. 增量递减while (interval >= 1) {// 3. 使用增量进行分组,开始遍历,执行插入排序// 此时由于引入了增量进行了分组,需要对插入排序进行改造for (let i = interval; i < len; i++) {// 4. 拿到当前元素,去与局部有序的元素进行比较,如果小于局部有序的元素就插入进去,(本例是从小到大排序)const temp = this.data[i]// 5. 记录当前元素的索引号,用于下一个 while 循环(与局部有序的元素进行比较的while循环)let j = i// 6. 当前元素与局部有序元素比较while (temp < this.data[j - interval] && (j - interval) >= 0) {this.data[j] = this.data[j - interval]j -= interval}// 7. 将当前元素插入进去this.data[j] = temp}interval = Math.floor(interval / 2)}}// 快速排序ArrayList.prototype.quickSort = () => {const quickSort = (data, left, right) => {// 0. 终止函数执行if (left >= right) return// 1. l,r 为此次排序 数组要进行排序的范围: 索引号:l~rlet l = left, r = right// 2. 将第一个元素作为基值const ele = data[l]// 3. 循环开始while (l < r) {// 4. 查询是否有小于基值的,小于基值的放在基值左边while (data[r] > ele && r > l) { // r > l 这个条件不能少,因为这个while循环会发生 r < l的情况r--}// 5. 查询是否有大于基值的,大于基值的放在基值右边while (data[l] <= ele && r > l) { // r > l 这个条件不能少,因为这个while循环会发生 r < l的情况l++}// 6. 跳出两个 while 循环,说明左边遇到大于基值的,右边遇到小于基值的// 交换位置const temp = data[l]data[l] = data[r]data[r] = temp}// 7. 跳出最外层 while 循环,说明 这个基值已经找到了在数组中正确的位置了 将基值放到正确的位置data[left] = data[l] // 这里要使用left,因为left才是第一个值,经历过while循环后l,r已经变化了,此时 l = rdata[l] = ele// 8. 将基值左右两边的数组序列进行快速排序quickSort(data, left, l - 1)quickSort(data, l + 1, right)}quickSort(this.data, 0, this.data.length - 1)}}const array = new ArrayList()












![[linux kernel]slub内存管理分析(7) MEMCG的影响与绕过](https://img-blog.csdnimg.cn/b42bfacfc4894c03a9f526c4041b23a7.gif#pic_center)