目录
一、选择排序
二、冒泡排序
三、插入排序
1. 希尔排序
四、归并排序
五、快速排序
版权声明:本文为博主原创文章,若文章中有错误请联系博主改正,请不要恶意留言(不喜欢请绕道)。欢迎大家转载,转载时请注明原文地址:https://blog.csdn.net/qq_37674616/article/details/82315651
目录
一、选择排序
二、冒泡排序
三、插入排序
1. 希尔排序
四、快速排序
我们衡量一个算法的指标包括:
-
时间复杂度 (在排序过程中需要比较和交换的次数)
-
空间复杂度 (在排序过程中需要的辅助存储空间)
-
稳定性 (该算法的实现是否可以保证排序后相等元素的初始顺序,只要该算法存在一种实现可以保证这种特征,那么该算法就是稳定的)
-
内部排序/外部排序 (在排序过程中数据元素是否完全在内存)
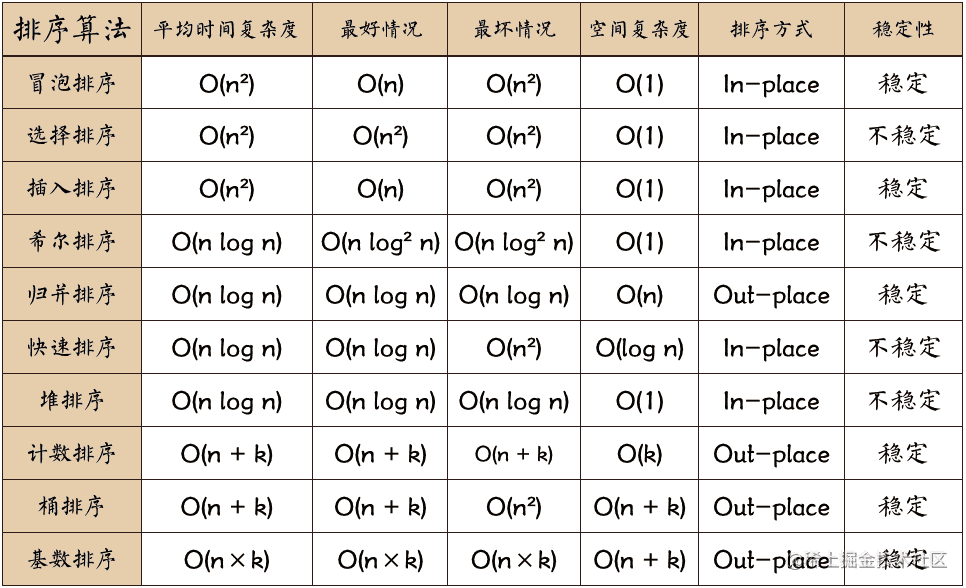
下表为各排序算法的性能标准:
一、选择排序
工作原理:初始时在未排序序列中找最小(最大)元素,放到序列的起始位置作为已排序序列;然后再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推。知道所有元素均排序完毕。
/*** @Author cc* @DateTime 2018-09-01* @param {arr} 未排序数组* @return {arr} 已排序数组* @description 选择排序*/function sort(arr){var len=arr.length;//已排序序列的末尾for(var i=0;i<len;i++){var min=i;//待排序序列for(var j=i+1;j<len;j++){//从待排序序列中找到最小值if(arr[j]<arr[min]){min=j;}}if(min!=i){var temp=arr[i];arr[i]=arr[min];arr[min]=temp;}}return arr;}//测试var arr=[1,4,35,3,2];sort(arr);console.log(arr); //[1,2,3,4,35]/*** @Author cc* @DateTime 2020-05-07* @param {nums} 未排序数组* @return {nums} 已排序数组* @description 选择排序*/
function insertionSort (nums) {for(let i=1;i<nums.length;i++){for(let j=0;j<i;j++){snapshot(nums)if(nums[i]<nums[j]){let temped=nums.splice(i,1);nums.splice(j,0,temped[0])}}}
}
该排序算法不稳定,最差时间复杂度 o(n^2);最优时间复杂度 o(n^2);平均时间复杂度 o(n^2)
二、冒泡排序
冒泡排序是一种简单的排序算法,它重复走访要排序的数列,一次比较两个元素,如果他们的的顺序错误就把他们调换过来,知道没有元素再需要交换,排序完成。
算法描述如下:
比较相邻的元素。如果第一个比第二个大,就交换他们;
对于每个相邻的元素重复相同的工作,知道最后一个元素,这样最后的元素会是最大的数
针对所有元素重复以上的步骤,除了最后一个元素
重复上面1~3步骤,知道排序结束
算法实现:
/*** @Author cc* @DateTime 2018-08-31* @param {arr} 待数组* @return {arr} 排好序的数组* @description 这是一个冒泡排序算法*/function bubbleSort(arr) {var len = arr.length;for (var i = 0; i < len - 1; i++) { //比较的趟数,每次将最大值放到数组最后for (var j = 0; j < len - i - 1; j++) { //将相邻的两个元素,两两比较if (arr[j]>arr[j+1]) { //元素交换值var temp=arr[j];arr[j]=arr[j+1];arr[j+1]=temp;}}}return arr;}var arr=[1,3,5,12,14,8,99];var result=bubbleSort(arr);console.log(result); //[1, 3, 5, 8, 12, 14, 99]辅助草图:
冒泡排序是稳定的排序算法,它的最差时间复杂度 o(n^2)即已排序数组;平均时间复杂度o(n^2),最优时间复杂度o(n)即在内部循环第一次运行时,使用一个旗标来表示该数组是不是已经是最小的了。
将上面代码做如下改动
/*** @Author cc* @DateTime 2020-05-07* @param {nums} 未排序数组* @return {nums} 已排序数组* @description 冒泡排序*/
function bubbleSort(nums) {do {var swapped = false; for (var i = 0; i < nums.length; i++) {if (nums[i] > nums[i+1]) {var temp = nums[i];nums[i] = nums[i+1];nums[i+1] = temp;swapped = true;}}} while(swapped);
}草图如下所示:
三、插入排序
工作原理:是通过构建有序序列,对未排序数组,在已排序序列中从后向前扫描,找到相应位置并插入。
算法描述:
1. 从第一元素开始,该元素可以默认已经被排序
2. 取出下一个元素,在已经排序序列中从后向前扫描
3. 如果已排序的元素大于新元素,将该元素移到下一个位置
4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
5.将新元素插入到该位置
6.重复2~5
/*** @Author cc* @DateTime 2018-09-01* @param {arr} 待排序序列* @return {arr} 排好序序列* @description 插入排序*/function insertSort(arr) {var len = arr.length;var preIndex, current;for (var i = 1; i < len; i++) {preIndex = i - 1; //排好序的数组最后一个下标current = arr[i]; //待排序的数值//让待排序的值与排序好的数组值进行比较while (preIndex >= 0 && arr[preIndex] > current) {arr[preIndex + 1] = arr[preIndex];preIndex--;}//待排序的数值大于等于排序好的值arr[preIndex + 1] = current;}return arr;}var arr=[8, 3, 5, 9, , 7, 1, 2 ];var result=insertSort(arr); //从小到大排序console.log(result); //[1, 2, 3, 4, 5, 6, 7, 8]
插入排序稳定,最差时间复杂度o(n^2)待排序列是降序序列;最优时间复杂度o(n)即待排序列是升序
平均时间复杂度o(n^2)
1. 希尔排序
希尔排序: 是对插入排序的改进,它与插入不同之处它会优先比较距离较远的元素
算法描述:
选择一个增量序列 t1,t2,...tk,其中ti>tj,tk=1;
按增量序列个数k,对序列进行k趟排序
每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m的子序列,分别对各自表进行直接插入排序.当增量因子为一时,整个序列被分为一组,算法终止。
/*** @Author cc* @DateTime 2018-09-01* @param {arr}* @return {arr} 已排序数组* @description 希尔排序*/function ShellSort(arr) {var len = arr.length;var temp, gap = 1;while (gap <= len / 3) {gap = gap * 3 + 1; //生成增量}while (gap >= 1) { //当分组变成成1时则排序完成for (var i = gap; i < len; i++) { //按增量循环数组temp = arr[i];//增量大于零且前面的数组的值大于后面数组的值则交换位置for (var j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {arr[j + gap] = arr[j];}arr[j + gap] = temp;}console.log(gap);gap = (gap - 1) / 3; //递减增量}return arr;}var arr = [5, 9, 2, 4,1,2,8,3,9,1];var result = ShellSort(arr);console.log(result);下图为增量为4时的内部数据交换图:
希尔排序稳定,时间复杂度为o(n^2),最优时间复杂度o(n)
四、归并排序
算法描述:
指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
算法思想:
采用分支法,递归地把当前序列平均分割成两半,然后再保证左右顺序情况下合并在一起。
/*** @Author cc* @DateTime 2020-05-07* @param {nums} 未排序数组* @return {nums} 已排序数组* @description 归并排序*/
function mergeSort(nums){if(nums.length<2) return nums;const middle=Math.floor(nums.length/2);const left=nums.slice(0,middle);const right=nums.slice(middle);return merge(mergeSort(left),mergeSort(right))
}const merge=(left,right)=>{const result=[]while(left.length&&right.length){if(left[0]>right[0]){result.push(right.shift())}else{result.push(left.shift())}}return result.concat(left,right);}五、快速排序
该方法的基本思想:
1. 从数列中取出一个数作为基数。
2. 重新排序数列,所有元素比基准值小的放到基准值前,所有元素比基准值大的放到其后。
3. 在对基准值左右区间,重复第二步,直到个区间只有一个数
算法实现:
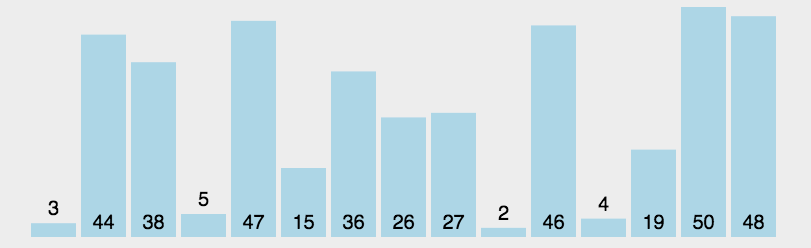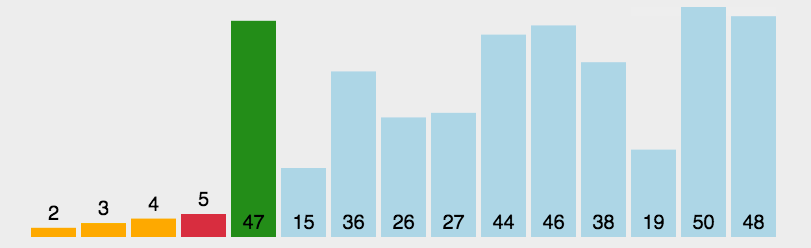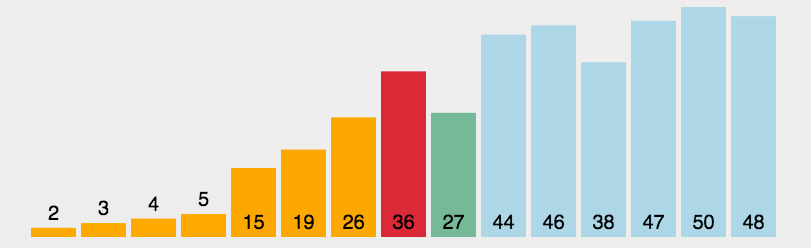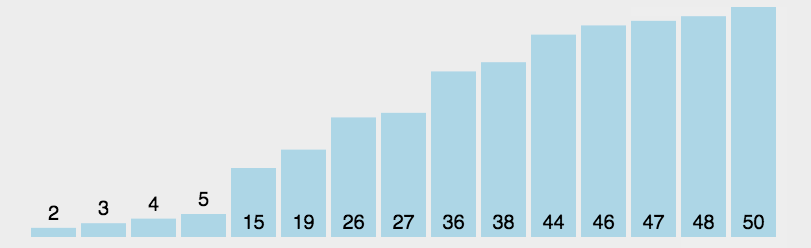
/*** @Author cc* @DateTime 2018-09-02* @param arr 待排序数组* @param left 数组第一个元素下标(0)* @param right 数组最后一个元素下标* @return arr 排好序的数组*/function quickSort(arr,left,right){if(left<right){var i=left,j=right;var x=arr[left]; //将基准数保存到 x 中while (i<j) {// 从右边向左边找小于x的数while(i<j && arr[j]>=x){j--;}if(i<j){arr[i]=arr[j];i++;}//从左边向右边找大于x的数while(i<j && arr[i]< x){i++;}if(i<j){arr[j]=arr[i];j--;}}arr[i]=x;console.log('i',i);console.log(x);console.log(arr);quickSort(arr,left,i-1);quickSort(arr,i+1,right);}return arr;}var arr=[3,2,45,12,4,3,12,4];console.log("原数组",arr);quickSort(arr,0,arr.length-1);console.log(arr); //[2, 3, 3, 4, 4, 12, 12, 45]下图为上面算的内部数据描述:
/*** @Author cc* @DateTime 2020-05-08* @param {nums} 未排序数组* @return {nums} 已排序数组* @description 快速排序*/function quickSort(nums){if(nums.length<2) return nums;const pivot=nums[nums.length-1];const left=[];const right=[];for(let i=0;i<nums.length-1;i++){if(nums[i]<pivot){left.push(nums[i])}else{right.push(nums[i])}}return [...quickSort(left),povit,...quickSort(right)]
}














![[linux kernel]slub内存管理分析(7) MEMCG的影响与绕过](https://img-blog.csdnimg.cn/b42bfacfc4894c03a9f526c4041b23a7.gif#pic_center)