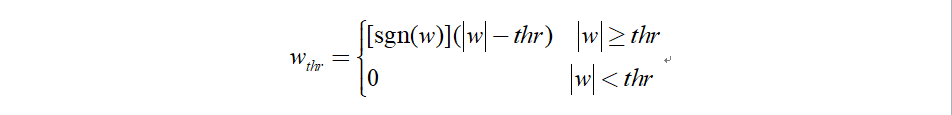目录
一、图像去噪基础知识
1. 图像去噪模型
2. 图像去噪类型
2.1 噪声类型——融合方式
2.2 噪声类型——概率分布
二、非局部均值图像去噪方法
三、基于图像先验的正则化去噪模型
1. 图像的梯度先验
2. 图像的非局部自相似先验
3. 图像的稀疏性先验
4. 图像的低秩性先验
一、图像去噪基础知识
1. 图像去噪模型
图像在传输、存储和拍摄等过程中,由于电磁波、传输设备存在杂质信号、镜头污渍等外部条件的干扰会产生噪声。从而导致图像不能清晰、真实地反映事物。
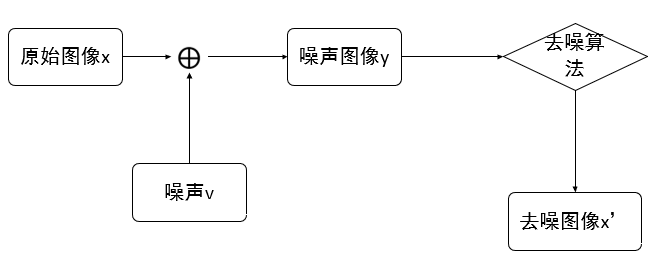
图像去噪算法地目的是将图像中的噪声去除,还原出无噪声的图像,并且最大限度地保存图像中原有的细节信息。通常图像去噪问题被当成一个逆问题来处理,给定一张M*N的噪声图像y,通过去噪算法去除图像噪声,恢复未被噪声污染过的图像x。噪声图像可用表达式:来表示。其中
表示图像噪声,图像去噪的模型如下图所示[1-3]。
2. 图像去噪类型
2.1 噪声类型——融合方式
噪声的分类方法多种多样,根据噪声与图像信息两者之间的融合方式,能够将噪声模型分成加性噪声和乘性噪声两类。假设给定观测到的噪声图像为, 原始图像为
,噪声为
,则加性噪声模型为:
乘性噪声模型为:
由噪声模型可以看出加性噪声和图像信号之间是相加的关系,不管有无图像信号的存在,噪声是客观存在的,因此可知图像信号和噪声信号之间是不相关的。而乘性噪声和图像信号之间是相乘的关系,图像信号存在,则噪声存在,图像信号不存在,噪声便不存在,故乘性噪声和图像信号之间是相关的。
2.2 噪声类型——概率分布
根据噪声服从的概率密度分布,可以将其分为高斯噪声、脉冲噪声和泊松噪声等。
(1)高斯噪声
高斯噪声是一类概率分布服从高斯分布的噪声,其概率密度为:
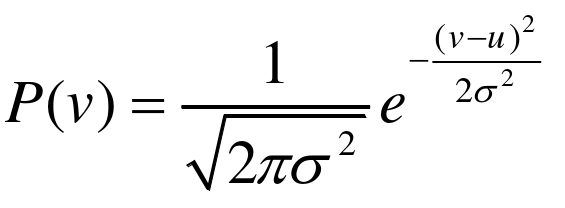
其中为噪声,
为噪声均值,通常取为0,
为噪声的标准差,由概率密度函数可以看出高斯噪声有很好的数学性质,该概率密度函数下函数的分布是对称的。现实生活中的噪声大多数能够近似表示为高斯噪声,因此通常研究者们在研究图像去噪算法时大多都使用均值为0,方差为
的高斯噪声模拟真实噪声。
(2)脉冲噪声
脉冲噪声的概率密度为:
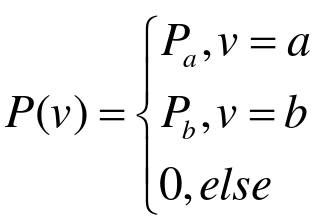
脉冲噪声点的亮暗程度与a、b的取值有关,当b>a时,则值为a的点表现为暗点,值为b的点表现为亮点。反之则值为b的是暗点,值为a的点是亮点。
(3)泊松噪声
泊松噪声的概率密度函数:
![]()
该概率密度下噪声的均值和方差都为,泊松噪声是因光量子测定时存在不确定性而导致的,因此泊松噪声一般在亮度很小或者高倍电子放大线路中会出现。
二、非局部均值图像去噪方法
目前已有的许多图像去噪方法大多是基于“局部平滑”(例如,传统的均值滤波器和高斯滤波器)。 虽然这类方法是有效的,但由于缺乏自适应性会导致图像模糊。从下面四幅灰度图像可以看出,它们都含有很多相似重复的纹理信息,考虑在大多数图像中出现的冗余信息,研究人员发现图像的自相似性可以应用于图像去噪领域。2005年,Buades等人首次提出了一种非局部均值(NLM)去噪算法。该算法充分利用图像中的自相似性达到去噪的目的,首先通过计算邻域间的欧式距离得到相似性权值,然后使用相似像素的加权平均得到去噪图像。这种计算权值的方法仅与图像块的相似性有关,与位置无关因此很好的避免了虚假纹理的产生。与传统的去噪算法相比,NLM算法具有算法简单、去噪性能好、易于改进和扩展的特点。


给定一个离散含噪图像,即:
其中,为去噪后的图像,
是以像素i为中心的方形搜索窗口,
为相似性权重系数,由像素点i和j的邻域相似性决定,该相似性通常利用图像块间的欧氏距离计算得到。因此,图像块相似性的度量如下所示,同时权值需要满足条件:
且
.
其中,,
表示以像素i为中心的图像块的灰度值,h控制指数函数的衰减速度并影响滤波程度。由上述公式可知权值
依赖于邻域窗口
e和
的相似度,当权值越大,图像的邻域就越相似。
非局部方法在去噪性能上优于局部方法,特别是对于高斯噪声。然而,NLM方法存在明显的不足,仍然有很大的改进空间,比如:较高的计算复杂度、相似性权重的计算公式受噪声影响较大和去噪参数确定不准等。
三、基于图像先验的正则化去噪模型
对于正则化去噪方法,最重要的一步是找到一个合适的自然图像先验。由于应用的领域不同,人们所关注的图像特征也是不同的,因此需要根据需求来构造合理的正则化去噪模型。在研究过程中,来自不同国家的学者针对图像自身先验进行约束,提出了不同形式的正则化去噪模型。下面介绍一些最有影响力的图像先验知识,包括梯度先验、非局部自相似性先验、稀疏性先验和低秩性先验。
1. 图像的梯度先验
最早将梯度先验引入图像去噪的是Tikhonov正则化方法,该方法根据原始图像是“平滑”这一假设进行去噪的。但是这种光滑约束是各向同性的,在去除噪声的过程中难免平滑掉大量边界以及细节结构。为了防止这种情况的发生。1992年,又有学者提出了基于TV的正则化方法来克服去噪图像的平滑性,这是该领域最有影响力的工作。TV正则项的本质是梯度的L1范数,定义为:
其中,是
的梯度。进而得到图像的去噪模型:
这种极小化问题也称为ROF模型,它具有以下几个优点:1)该模型存在唯一解;2)关于x的解空间函数是不连续函数,即允许存在边缘位置的特殊像素点,所以在去噪过程中能较好地保持边缘。由于以上优点,TV模型被广泛用于图像去噪。但是模型也存在着缺陷:1)由于TV模型沿像素梯度方向是平滑地,容易将噪声当作伪纹理而被保存下,因此在平坦区域易产生阶梯效应;2)由于TV模型逐个相邻像素点计算像素差,会导致图像纹理趋于过平滑;3)TV模型中正则化参数的选择是依赖于经验值的,因此选择合适的参数值存在一定的难度。下图是利用了TV正则化后的视频数据恢复算法(HSR-TT)的对比图,选择视频的大小为256*256*30,我们选择第10帧作为对比[5]。

2. 图像的非局部自相似先验
基于自然图像在不同位置包含大量相似图像这一事实,一系列方法利用了图像的非局部自相似(NSS)先验进行去噪。这类正则化去噪模型的开创性工作就是上面所讲的NLM去噪。通过将NLM中的第一步,即像素相关性的估计,视为图像相关图的构成方法,开发了各种形式的基于图拉普拉斯的正则化方法。根据前面介绍的相似性度量公式,NSS先验定义为:
其中,是由在一个搜索窗口内所有围绕像素
的中心像素形成的列向量,
是一个包含所有相应权重
的列向量。 尽管这类去噪算法取得了巨大的成功,但它们往往无法保持细致的纹理,着极大地降低了图像地视觉质量。
3. 图像的稀疏性先验
由于自然图像具有冗余性,因此可以用字典进行稀疏表示。根据此先验知识,基于冗余字典的稀疏表示的去噪算法已成为近年来研究的热点问题。无噪声图像在字典下表示是稀疏的,而噪声随机的是不可稀疏的,因此图像信息蕴含在少量的系数中。
图像稀疏表示的数学模型是,将输入图像块分解为矩阵D与向量
的乘积形式,其中矩阵D由一组基向量组成,向量α中大部分元素为零。由于传统的正交基对图像稀疏表示能力有限,有学者提出了字典的概念,用过完备字典代替正交小波基。这使得图像在冗余基库中可以方便地选择基向量,以更好地实现对复杂图像的稀疏表示。

稀疏表示模型的求解可以转化为优化问题,用L1范数约束,即
。通用的稀疏表示模型为
其中,是包含稀疏系数向量的矩阵。
稀疏表示模型提供了观察图像的一个新视角,特别是超完备字典的引入更有利于反映图像复杂的结构信息,但它忽略了图形的自相似性。而且,字典的训练过程是非常费时的,同时如何合理求解稀疏表示系数也是该模型的一个重要问题。
4. 图像的低秩性先验
与稀疏表示模型不同,低秩模型将相似的图像块重组为一个矩阵,矩阵每一个列都是一个展开的图像块向量,并利用相似块矩阵的低秩性先验进行图像去噪。
对于一幅含噪图像y,将每组相似图像块向量化成列向量构成矩阵Y()。我们可以将矩阵Y看作是无噪矩阵X受加性噪声矩阵N干扰后的结果,其中矩阵X的列向量之间相关性很高,具有低秩的性质。在加性噪声模型下,含噪矩阵满足Y=X+N,其中N是随机的噪声干扰矩阵,通常情况下N是满秩的。用于含噪图像恢复的低秩方法可以分成两类:基于低秩矩阵分解的方法和基于核范数最小化的方法。
第一类方法是以SVD分解为核心的,通过限制奇异值的数量或者大小来约束矩阵结构的稀疏性,从而给出图像块矩阵的低秩逼近。
对降噪矩阵的估计需要解决的问题是用一个秩为k的低秩矩阵逼近含噪矩阵
,该逼近基于
与
之间差异的F范数进行最小化且以
作为约束:
上面问题可以由Y的奇异值分解解决,由于奇异值分解的能量压缩性质,信息的主要能量都集中在少数几个较大的奇异值上,而较小的奇异值对应于噪声子空间,将它们设置为零可以得到去噪后的低秩矩阵,问题的关键是如何确定阈值来区分信号与噪声,太大的阈值会使图像过于平滑从而模糊掉边缘及纹理,太小的阈值则难以达到去噪的效果。
另一类使基于核范数最小化(NNM)的方法,该方法以F范数作为数据保真项,可以采用含噪矩阵奇异值的软阈值操作来求解。核范数最小化模型为:
其中,表示F范数,并且
,这里
表示X的第i个奇异值。尽管核范数最小化已被广泛应用于解决低秩矩阵逼近的问题,它仍存在一些不足。每个奇异值的权重相等,并且对每个奇异值应用相同的阈值收缩,但是不同的奇异值具有不同的重要性。因此就有学者提出了基于核范数最小化的WNNM模型,该模型可以自适应地将权重分配给不同大小地奇异值,并使用软阈值方法对其进行去噪。给定一个权重向量
,加权核范数最小化模型可表示为:
其中,。WNNM方法综合考虑了噪声在整个奇异值空间内的能量分布,显示了最先进的去噪结果。但由于WNNM的迭代增强步骤收敛到噪声图像并且迭代次数固定在经验值上,导致计算成本相对较高。此外,WNNM为噪声图像中给定的参考图像块寻找相似块时不考虑噪声因素,导致块匹配可能与参考图像块不完全相似。
上面大多数被提及的方法通过对图像先验进行建模来解决,例如,基于梯度(例如总变差),非局部自相似(例如非局部均值),稀疏建模(例如图像块字典学习)和低秩性(例如加权核范数最小化)。然而,这些技术仍然受到重大限制,例如没有充分挖掘图像特征信息。基于梯度先验去噪方法的重点是局部特征,而忽略图像的全局结构。在许多情况下,这可能会使图像产生阶梯效应。同样,基于非局部自相似性的方法通常采用图像块加权平均,容易导致过度平滑图像。
[1]袁媛. 基于非局部自相似性的去噪算法研究[D].华东师范大学,2018.
[2]范琳伟. 基于非局部均值和正则化模型的图像去噪研究[D].山东大学,2019.
[3]邵欧阳. 基于非局部自相似性和低秩近似理论的地震数据去噪方法研究[D].中国地质大学,2021.DOI:10.27492/d.cnki.gzdzu.2021.000138.
[4]白同磊,张翠芳.外部非局部自相似先验的图像去噪[J].电讯技术,2021,61(02):211-217.
[5]Jing-Hua Yang, Xi-Le Zhao, Tian-Hui Ma, Meng Ding, Ting-Zhu Huang, Tensor train rank minimization with hybrid smoothness regularization for visual data recovery, Applied Mathematical Modelling, Volume 81, 2020,