01背包问题是最基本的背包问题,它包含了背包问题中设计状态、方程的最基本思想,另外,别的类型的背包问题往往也可以转换成01背包问题求解。
dd大牛的文章中这样提到01背包问题:
题目
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
基本思路
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
用子问题定义状态:即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是:f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}。
这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下:“将前i件物品放入容量为v的背包中”这个子问题,若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中”;如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”,此时能获得的最大价值就是f [i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。
注意f[i][v]有意义当且仅当存在一个前i件物品的子集,其费用总和为v。所以按照这个方程递推完毕后,最终的答案并不一定是f[N] [V],而是f[N][0..V]的最大值。如果将状态的定义中的“恰”字去掉,在转移方程中就要再加入一项f[i][v-1],这样就可以保证f[N] [V]就是最后的答案。至于为什么这样就可以,由你自己来体会了。
优化空间复杂度
以上方法的时间和空间复杂度均为O(N*V),其中时间复杂度基本已经不能再优化了,但空间复杂度却可以优化到O(V)。
先考虑上面讲的基本思路如何实现,肯定是有一个主循环i=1..N,每次算出来二维数组f[i][0..V]的所有值。那么,如果只用一个数组f [0..V],能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢?f[i][v]是由f[i-1][v]和f[i-1] [v-c[i]]两个子问题递推而来,能否保证在推f[i][v]时(也即在第i次主循环中推f[v]时)能够得到f[i-1][v]和f[i-1][v -c[i]]的值呢?事实上,这要求在每次主循环中我们以v=V..0的顺序推f[v],这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i -1][v-c[i]]的值。伪代码如下:
for i=1..N
for v=V..0
f[v]=max{f[v],f[v-c[i]]+w[i]};
其中的f[v]=max{f[v],f[v-c[i]]}一句恰就相当于我们的转移方程f[i][v]=max{f[i-1][v],f[i- 1][v-c[i]]},因为现在的f[v-c[i]]就相当于原来的f[i-1][v-c[i]]。如果将v的循环顺序从上面的逆序改成顺序的话,那么则成了f[i][v]由f[i][v-c[i]]推知,与本题意不符,但它却是另一个重要的背包问题P02最简捷的解决方案,故学习只用一维数组解01背包问题是十分必要的。
01背包问题 Acwing 02
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
朴素版解法:二维空间解法
每件物品只能选一次,对于每种物品,我们有两种选择
1.不选第i个物品 -> f[i][j]=f[i-1][j]
等于选前i-1个物品,空间为j情况下的最优解
2.选第i个物品 -> f[i][j]=f[i-1][j-v[i]]+w[i]
如果选的话,前i-1个物品的体积最多为j-v[i]
在这两种情况中取较大值即可,即为当前情况的最优解。
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N=1010;int n,m;
int f[N][N]; //f[i][j]表示前i个物品,背包容量是j的情况下的最大价值。
int w[N];
int v[N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>w[i];for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);} int res=0;for(int i=0;i<=m;i++)res=max(res,f[n][i]);cout<<res<<endl;return 0;
}
解法二:滚动数组优化:(只需要一个数组)
状态转移每次只与上一层有关,所以用一个一维数组就可以
转移方程:f[i]=max(f[i],f[i-v[i]]+w[i])
其实就相当于二维中的 f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i])
所以第二层循环需要从大到小循环,因为若是继续从小到大循环,后面算的时候,用的是这一层已经算过的数据,就变成f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]) ,(这正好是完全背包一维的解法,每个物品可以选无限次)而从大到小算的话一定用的是上一层的状态
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N=1010;int n,m;
int f[N];
int w[N];
int v[N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);cout<<f[m]<<endl;return 0;
}
这时的f[i]表示空间<=i的最大价值,所以最后直接输出dp[m]即可,
若题目要求装满背包,即将物品恰装入一个容量为m的背包中,只需要将初始化条件改一改即可,----将dp数组初始化为负无穷,f[0]=0,即可确保状态一定是从0转移过来的。





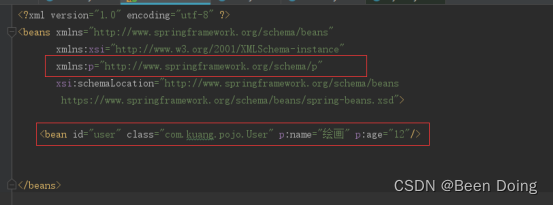
![[Spring] IoC的理解及三种依赖注入方式](https://img-blog.csdnimg.cn/b4272c1fb3784a96a48cce9960cb9ec4.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ2xvdWRlZWVlZQ==,size_20,color_FFFFFF,t_70,g_se,x_16)