背包九讲.

article/2025/9/14 21:13:11

背包九讲

  • 背包问题
  • 完全背包问题
  • 多重背包问题 I
  • 多重背包问题 II
  • 多重背包问题 III
  • 混合背包问题
  • 二维费用的背包问题
  • 分组背包问题
  • 有依赖的背包问题
  • 背包问题求方案数
  • 背包问题求具体方案

背包问题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N,V ≤ 1000
0 < vi,wi ≤ 1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N][N];
int v[N], w[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ ){f[i][j] = f[i - 1][j];if (j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);}cout << f[n][m] << endl;return 0;
}

完全背包问题

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N,V ≤ 1000
0 < vi,wi ≤ 1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ ){f[i][j] = f[i - 1][j];if (j >= v[i])f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);}cout << f[n][m] << endl;return 0;
}

多重背包问题 I

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N,V ≤ 100
0 < vi,wi,si ≤ 100

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

#include <iostream>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ ) for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);cout << f[n][m] << endl;return 0;
}

#include <iostream>
using namespace std;
const int N = 10010;
int n, m, cnt = 1;
int v[N], w[N];
int f[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) {int a, b, c;cin >> a >> b >> c;for (int j = 1; j <= c; j ++ ){v[cnt] = a;w[cnt] = b;cnt ++ ;}}for (int i = 1; i <= cnt; i ++ )for (int j = m; j >= v[i]; j -- ){f[j] = max(f[j], f[j - v[i]] + w[i]);}cout << f[m] << endl;return 0;
}

多重背包问题 II

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N ≤ 1000
0 < V ≤ 2000
0 < vi,wi,si ≤ 2000

提示：
本题考查多重背包的二进制优化方法。

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

#include <iostream>
#include <vector>
using namespace std;
const int N = 2010;
int n, m;
int f[N];
struct Good
{int v, w;
};
vector<Good> goods;
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){int v, w, s;cin >> v >> w >> s;for (int k = 1; k <= s; k *= 2 ) {s -= k;goods.push_back({v * k, w * k});}if (s > 0) goods.push_back({s * v, s * w});}for (auto good : goods)for (int j = m; j >= good.v; j -- )f[j] = max(f[j], f[j - good.v] + good.w);cout << f[m] << endl;return 0; 
}

多重背包问题 III

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V (0 < N ≤ 1000, 0 < V ≤ 20000)，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N ≤ 1000
0 < V ≤ 20000
0 < vi,wi,si ≤ 20000

提示
本题考查多重背包的单调队列优化方法。

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

男人八题

在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20010;
int n, m;
int f[N], g[N], q[N];
int main()
{cin >> n >> m;for (int i = 0; i < n; i ++ ){int v, w, s;cin >> v >> w >> s;memcpy(g, f, sizeof f);for (int j = 0; j < v; j ++ ){int hh = 0, tt = -1;for (int k = j; k <= m; k += v){if (hh <= tt && q[hh] < k - s * v) hh ++ ;while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v* w) tt -- ;q[ ++ tt] = k;f[k] = g[q[hh]] + (k - q[hh]) / v * w;}}}cout << f[m] << endl;return 0;
}

混合背包问题

有 N 种物品和一个容量是 V 的背包。

物品一共有三类：

  • 第一类物品只能用1次（01背包）；
  • 第二类物品可以用无限次（完全背包）；
  • 第三类物品最多只能用 si 次（多重背包）；

每种体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

  • si=−1 表示第 i 种物品只能用1次；
  • si=0 表示第 i 种物品可以用无限次；
  • si>0 表示第 i 种物品可以使用 si 次；

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N,V ≤ 1000
0 < vi,wi ≤ 1000
−1 ≤ si ≤ 1000

输入样例

4 5
1 2 -1
2 4 1
3 4 0
4 5 2

输出样例：

8

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], s[N];
int f[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];for (int i = 1; i <= n; i ++ ){if (s[i] == 0) for (int j = v[i]; j <= m; j ++ )f[j] = max(f[j], f[j - v[i]] + w[i]);else {if (s[i] == -1) s[i] = 1;for (int k = 1; k <= s[i]; k *= 2){for (int j = m; j >= k * v[i]; j -- )f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);s[i] -= k;}if (s[i])for (int j = m; j >= s[i] * v[i]; j -- )f[j] = max(f[j], f[j - s[i] * v[i]] + s[i] * w[i]);}}cout << f[m] << endl;return 0;
}

二维费用的背包问题

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。

每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

输入格式
第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N ≤ 1000
0 < V,M ≤ 100
0 < vi,mi ≤ 100
0 < wi ≤ 1000

输入样例

4 5 6
1 2 3
2 4 4
3 4 5
4 5 6

输出样例：

8

在这里插入图片描述

#include <iostream>
using namespace std;
const int NU = 1010;
int N, V, M;
int v[NU], m[NU], w[NU];
int f[NU][NU];
int main()
{cin >> N >> V >> M;for (int i = 1; i <= N; i ++ ) cin >> v[i] >> m[i] >> w[i];for (int i = 1; i <= N; i ++ )for (int j = V; j >= v[i]; j -- )for (int k = M; k >= m[i]; k -- )f[j][k] = max(f[j][k], f[j - v[i]][k - m[i]] + w[i]);cout << f[V][M] << endl;return 0;
}

分组背包问题

三重循环

  1. 物品种类
  2. 枚举背包体积
  3. 枚举决策：当前种类物品的数量

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式
第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N 组数据：

  • 每组数据第一行有一个整数 Si，表示第 i 个物品组的物品数量；
  • 每组数据接下来有 Si 行，每行有两个整数 vij,wij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式
输出一个整数，表示最大价值。

数据范围
0 < N,V ≤ 100
0 < Si ≤ 100
0 < vij,wij ≤ 100

输入样例

3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例：

8

在这里插入图片描述

没完全搞懂

分组背包问题，先枚举物品组，然后枚举体积，内部枚举决策

#include <iostream>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N];
int f[N];
int main()
{cin >> n >> m;for (int i = 0; i < n; i ++ ) // 物品组{int s;cin >> s;for (int j = 0; j < s; j ++ ) cin >> v[j] >> w[j];for (int j = m; j >= 0; j -- ) // 体积for (int k = 0; k < s; k ++ ) // 决策 if (j >= v[k])f[j] = max(f[j], f[j - v[k]] + w[k]);}cout << f[m] << endl;return 0;
}

有依赖的背包问题

有 N 个物品和一个容量是 V 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：
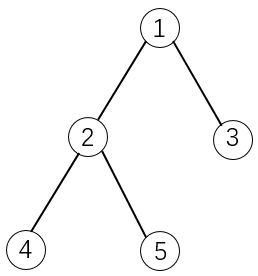
在这里插入图片描述
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式
第一行有两个整数 N，V，用空格隔开，分别表示物品个数和背包容量。

接下来有 N 行数据，每行数据表示一个物品。
第 i 行有三个整数 vi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1，表示根节点。 数据保证所有物品构成一棵树。

输出格式
输出一个整数，表示最大价值。

数据范围
1 ≤ N,V ≤ 100
1 ≤ vi,wi ≤ 100
父节点编号范围：

  • 内部结点：1 ≤ pi ≤ N;
  • 根节点 pi=−1;

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

11

在这里插入图片描述
每个节点求一个分组背包

没完全懂

#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];
void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{for (int i = h[u]; ~ i; i = ne[i]) // 物品组 {int son = e[i];dfs(e[i]);// 分组背包 for (int j = m - v[u]; j >= 0; j -- ) // 体积for (int k = 0; k <= j; k ++ ) // 决策f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);	 }// 加入u for (int i = m; i >= v[u]; i -- ) f[u][i] = f[u][i - v[u]] + w[u];for (int i = 0; i < v[u]; i ++ ) f[u][i] = 0; 
}
int main()
{int root;cin >> n >> m;memset(h, -1, sizeof h);for (int i = 1; i <= n; i ++ ){int p;cin >> v[i] >> w[i] >> p;if (p == -1) root = i;else add(p, i);}dfs(root);cout << f[root][m] << endl;return 0;
}

背包问题求方案数

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 最优选法的方案数。注意答案可能很大，请输出答案模 109+7 的结果。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示 方案数 模 109+7 的结果。

数据范围
0 < N,V ≤ 1000
0 < vi,wi ≤ 1000

输入样例

4 5
1 2
2 4
3 4
4 6

输出样例：

2

在这里插入图片描述

没完全掌握

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n, m;
int v[N], w[N];
int f[N], g[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];memset(f, -0x3f, sizeof f);f[0] = 0;g[0] = 1;for (int i = 1; i <= n; i ++ )for (int j = m; j >= v[i]; j -- ){int maxv = max(f[j], f[j - v[i]] + w[i]);int s = 0;if (f[j] == maxv) s = g[j];if (f[j - v[i]] + w[i] == maxv) s = (s + g[j - v[i]]) % mod;f[j] = maxv;g[j] = s;}	int res = 0;for (int i = 1; i <= m; i ++ )if (f[i] > f[res])res = i;int sum = 0;		for (int i = 0; i <= m; i ++ )if (f[i] == f[res])sum = (sum + g[i]) % mod;cout << sum << endl;return 0;
}

背包问题求具体方案

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 1…N。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一行，包含若干个用空格隔开的整数，表示最优解中所选物品的编号序列，且该编号序列的字典序最小。

物品编号范围是 1…N。

数据范围
0 < N,V ≤ 1000
0 < vi,wi ≤ 1000

输入样例

4 5
1 2
2 4
3 4
4 6

输出样例：

1 4

没完全掌握

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = n; i >= 1; i -- )for (int j = 0; j <= m; j ++ ) {f[i][j] = f[i + 1][j];if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);}int j = m;for (int i = 1; i <= n; i ++ ) if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]){cout << i << ' ';j -= v[i];}return 0;
}

http://chatgpt.dhexx.cn/article/k3jlA6dL.shtml

相关文章

背包九讲——全篇详细理解与代码实现

背包九讲——全篇详细理解与代码实现

DD_engi 背包九讲的个人整理 写在前面 Last Modified:2021/9 博主重新审读了一下整篇文章&#xff0c;以我现在更进一步的理解更新了文章中的部分内容&#xff0c;有问题及疑惑可随时评论或私信&#xff0c;会及时回复&#xff01;&#xff01;! 更新进度&#xff1a;9/9:⑦有…
阅读更多...
22 springboot依赖注入三种方式

22 springboot依赖注入三种方式

1 基于构造函数的依赖注入 Spring 基于构造函数的依赖注入_w3cschoolJ虽然当前有关Spring Framework&#xff08;5.0.3&#xff09;的文档仅定义了两种主要的注入类型&#xff0c;但实际上有三种 public class UserServiceImpl implents UserService{private UserDao userDa…
阅读更多...
Spring实现依赖注入的几种方式

Spring实现依赖注入的几种方式

Spring实现依赖注入的几种方式 1.基于有参构造实现 <bean id"user" class"com.ccu.twj"><constructor-arg name"name" value"张三"></constructor-arg><constructor-arg name"age" value"18&quo…
阅读更多...
依赖注入三种方式

依赖注入三种方式

1.构造器函数注入 分为无参构造方法和有参构造方法两种方式&#xff0c;其中有参构造方法又包含三种方式。 有参构造的三种方式&#xff1a; 下标赋值参数类型赋值参数名赋值 案例&#xff1a; User.java public class User {private String name;private String mess;pub…
阅读更多...
spring依赖注入的三种方式以及优缺点

spring依赖注入的三种方式以及优缺点

spring依赖注入的三种方式以及优缺点 一.依赖注入的三种方式 1.通过构造器注入。&#xff08;spring4.3之后&#xff0c;推荐使用&#xff09; 2.通过setter注入。&#xff08;spring4.3之前&#xff0c;推荐使用&#xff09; 3通过filed注入。 二.三种方式的代码示例&…
阅读更多...
依赖注入的三种方式和循环依赖的产生

依赖注入的三种方式和循环依赖的产生

什么是循环依赖 说白了就是对象之间的依赖关系成环 例如A->B,B->C,C->A&#xff0c;并不限于对象的多少&#xff0c;最终成环就是循环依赖&#xff0c;也因此循环依赖的发生可能是十分复杂的。&#xff0c;如果使用属性注入的话&#xff0c;开发过程中甚至很难察觉。…
阅读更多...
[Spring] IoC的理解及三种依赖注入方式

[Spring] IoC的理解及三种依赖注入方式

[Spring] IoC的理解及三种依赖注入方式 Spring---IoC的理解及三种依赖注入方式IoC是什么意思依赖控制反转 Spring提供的依赖注入的三种方式setter注入&#xff08;属性注入&#xff09;构造器注入p命名空间注入&#xff08;工厂方法注入&#xff09; Autowired Spring—IoC的理…
阅读更多...
Spring依赖注入的三种方式

Spring依赖注入的三种方式

目录 一、变量注入&#xff08;Field Injection&#xff09; 二、构造器注入&#xff08;Constructor Injection&#xff09; 三、setter方法注入 &#xff08;Setter Injection&#xff09; 四、使用场景 Spring的依赖注入&#xff0c;我们一般使用Autowired注解来完成&am…
阅读更多...
依赖注入的三种方式

依赖注入的三种方式

DI(依赖注入) 注入的三种方法&#xff1a;构造器方法注入&#xff0c;set注入&#xff0c;基于注解的注入&#xff08;接口注入&#xff09; 1&#xff1a;构造器方法注入 创建一个Address类&#xff1b; public class Address {private String address;public Address() {}pu…
阅读更多...
Pubmedy的使用教程

Pubmedy的使用教程

使用方法如下&#xff1a; 使用前先配置Sci-Hub的地址&#xff0c;如果网址不失效&#xff0c;配置一次即可 选中文章的DOI&#xff0c;右击选择Sci-Hub Search即可自动跳转到文章对应的Sci-Hub界面
阅读更多...
Pubmedy加载时显示程序包无效的解决方案

Pubmedy加载时显示程序包无效的解决方案

目前谷歌应用商城已经下架Pubmedy&#xff0c;本地安装又遇到程序包无效&#xff1a;“CRX_HEADER_INVALID”。 解决方案&#xff1a; 将PubMedy.crx重命名为PubMedy.rar或者PubMedy.zip解压到要安装的位置找到扩展程序选项&#xff0c;并启用开发者选项选择加载已解压的扩展程…
阅读更多...
细胞实验文献检索——PubMed | MedChemExpress

细胞实验文献检索——PubMed | MedChemExpress

今天我们就以小白的课题——自噬 (Autophagy) 为例&#xff0c;给大家展示一波。这个时候给大家隆重介绍我们的——PubMed。 PubMed 提到 PubMed&#xff0c;相信大家应该都不陌生&#xff0c;它是常用的国外数据库之一&#xff0c;也是小编查找文献最喜欢的工具。自成立以来…
阅读更多...
免费获取论文全文的方法，SCI-HUB的使用教程

免费获取论文全文的方法，SCI-HUB的使用教程

很多人不在学校期间需要看文献全文&#xff0c;很多人获取文章的方式或是在网上求助或是给原作者索要。在SCI—HUB出现后&#xff0c;这些麻烦都不需要。SCI—PUB上保存了超过了4700万篇科研文献。SCI—PUB的网址 使用方法&#xff1a; 方法一、打开网页将想要论文的URL地址&…
阅读更多...
SCI-HUB丨最新文献网址

SCI-HUB丨最新文献网址

sci-hub&#xff1a;在我们获取文献与学术论文的道路上提供了极好的便利&#xff0c;可以从中得到免费的文献下载&#xff0c;但也因为这样遭到各大出版社&#xff1a;ai思为尔&#xff0c;施普林格&#xff0c;wiley等出版社的打击与封杀&#xff0c;使得Sci-Hub在域名上不得不…
阅读更多...
pubmed显示服务器不稳定,PubMed天天用，可是你真的用对了吗？

pubmed显示服务器不稳定,PubMed天天用，可是你真的用对了吗？

你是用关键词在PubMed上找论文的吗&#xff1f;如果关键词好几个&#xff0c;由于单词间的空格键存在AND命令&#xff0c;导致明明要搜的是词组&#xff0c;搜索不是被放大就是缩小&#xff0c;很难检索到合适量且关联度高的文。例如&#xff0c;你想找和肠炎与肿瘤坏死因子相关…
阅读更多...
pubmed文献批量化下载器

pubmed文献批量化下载器

1.代码如下 import time import requests import pandas as pd import osdef getArticle(PMCID,NIHMSID,DOI,title,path):print(PMCID,NIHMSID,DOI,title,path)os.chdir(path)headers {"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit…
阅读更多...
PubMed插件：分区、影响因子和即时IF一目了然，还能秒下文献(亲测有效)

PubMed插件：分区、影响因子和即时IF一目了然，还能秒下文献(亲测有效)

Pubmed作为生物医药研究者最常用的免费文摘数据库&#xff0c;素有检索江湖上的泰山北斗之称&#xff0c;用好Pubmed&#xff0c;其他一切pubmed镜像网站都是浮云。今天小编给大家介绍一款完全免费的无需登录的pubmed插件&#xff0c;他可以解决pubmed本身不显示杂志影响因子的…
阅读更多...
干货分享|被PubMed收录的论文，在MEDLINE和SCIE能检索到吗？

干货分享|被PubMed收录的论文，在MEDLINE和SCIE能检索到吗？

PubMed PubMed是由美国国家医学图书馆&#xff08;National Library of Medicine&#xff0c;NLM&#xff09;的国家生物技术信息中心&#xff08;National Center for Biotechnology Information&#xff0c;NCBI&#xff09;开发研制的一个医学文献网络数据库。PubMed是当今…
阅读更多...
MEDLINE与PubMed有什么区别？检索范围包含哪些？

MEDLINE与PubMed有什么区别？检索范围包含哪些？

PubMed PubMed是由美国国家医学图书馆&#xff08;National Library of Medicine&#xff0c;NLM&#xff09;的国家生物技术信息中心&#xff08;National Center for Biotechnology Information&#xff0c;NCBI&#xff09;开发研制的一个医学文献网络数据库。 PubMed是当今…
阅读更多...
怎么找生物信息论文的数据，PubMed太有用了！

怎么找生物信息论文的数据，PubMed太有用了！

小白的创作灵感日志&#xff1a; 由于要跑通一篇Paper A的代码&#xff0c;我需要找到它用到的所有数据集&#xff0c;今天我要找的是 Nagano 细胞周期数据集&#xff0c;刚开始脑子一团浆糊&#xff0c;直接在谷歌上搜“Nagano”&#xff0c;出来的全都是日本的一个名叫Nagano…
阅读更多...
推荐文章

Copyright @ 2022~2023