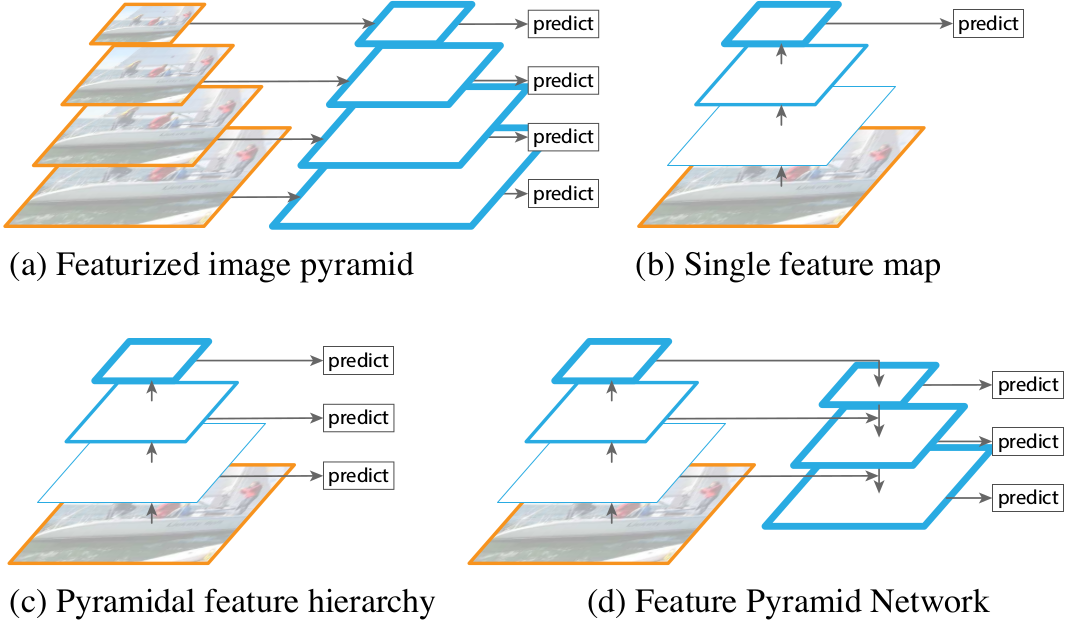
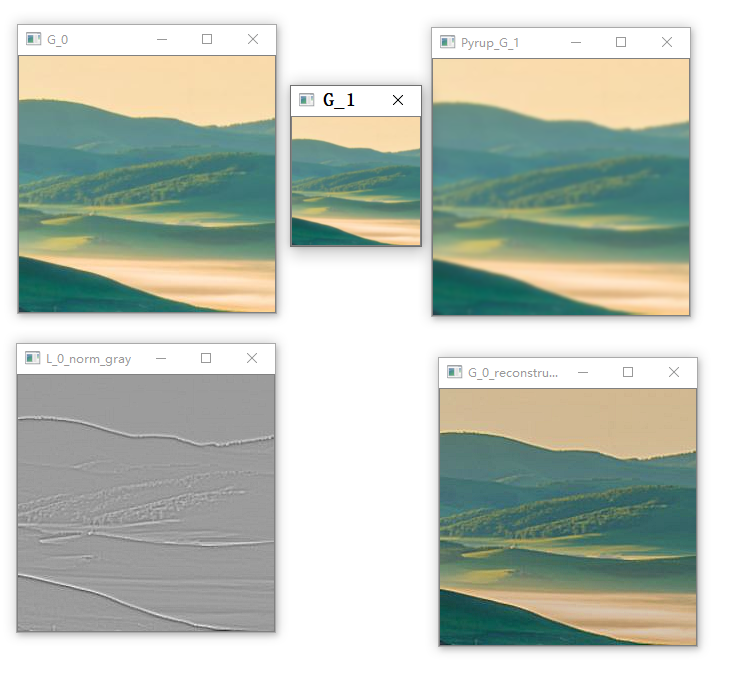
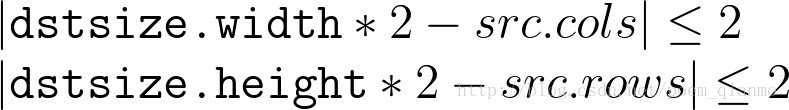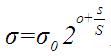1、高斯金字塔计算步骤
(1)对第 i i i 层图像进行高斯内核卷积;
(2)将所有偶数行和列去除(下采样),得到第 i + 1 i+1 i+1 层图像;
(3)对原始图像不停迭代以上步骤就能得到整个金字塔。
2、拉普拉斯金字塔计算步骤
(1)将第 i i i 层图像在每个方向扩大为原来的两倍(上采样),新增的行和列以0填充;
(2)使用先前同样的内核(乘以4)与放大后的图像卷积,获得“新增像素”的近似值,得到第 i − 1 i-1 i−1 层图像;
(3)与高斯金字塔第同层次图像相减,就是图像在缩小和放大整个过程中减少的信息,称为拉普拉斯残差金字塔。
3、Matlab程序实现
close all
clear
clcimg=imread('lena.png');
img_gray=rgb2gray(img);
img_filter=double(img_gray);
%% 设置金字塔层数:p,高斯金字塔元胞数组为gausPyramid,拉普拉斯金字塔元胞数组为LaplPyramid
p=4;
gausPyramid=cell(1,p);
LaplPyramid=gausPyramid;%% 5*5高斯核,sigma=1
kernel=fspecial('gaussian',5,1);
% 高斯核乘以4(亮度守恒)
kernel1=4.*kernel;%% 计算gausPyramid和LaplPyramid
[m,n]=size(img_filter);
gausPyramid(1)=mat2cell(img_filter,m,n);
for i=2:p %% 高斯金字塔% 滤波img_filter1=filter2(kernel,img_filter,'same');% 下采样:去掉偶数行、列img_filter1(2:2:end,:)=[];img_filter1(:,2:2:end)=[]; [m,n]=size(img_filter1);gausPyramid(i)=mat2cell(img_filter1,m,n);%% 拉普拉斯金字塔% 上采样:新增全零行、列img_filter2=zeros(2*m,2*n);img_filter2(1:2:2*m,1:2:2*n)=img_filter1(1:m,1:n);% 滤波img_filter2=filter2(kernel1,img_filter2,'same');img_filter2=img_filter-img_filter2;LaplPyramid(i-1)=mat2cell(img_filter2,2*m,2*n);img_filter=img_filter1;
end
LaplPyramid(p)=gausPyramid(p);%% 显示金字塔,把元胞金字塔统计到一个数组中
img_gaus=cell2mat(gausPyramid(1));
[r,~]=size(img_gaus);
img_lapl=cell2mat(LaplPyramid(1));
[r1,~]=size(img_lapl);
for i=2:p%% 高斯金字塔img_filter=cell2mat(gausPyramid(i));[m,~]=size(img_filter);% 在第一行前面补(r-m)行全255行,10列全255列,与最大的图像行对齐img_filter=padarray(img_filter,[r-m 10],255,'pre');img_gaus=[img_gaus img_filter];%% 拉普拉斯金字塔img_filter=cell2mat(LaplPyramid(i));[m,~]=size(img_filter);% 在第一行前面补(r-m)行全255行,10列全255列,与最大的图像行对齐img_filter=padarray(img_filter,[r1-m 10],255,'pre');img_lapl=[img_lapl img_filter];
end
figure('Name','gausPyramid');
imshow(uint8(img_gaus));
figure('Name','LaplPyramid');
imshow(uint8(abs(img_lapl)));
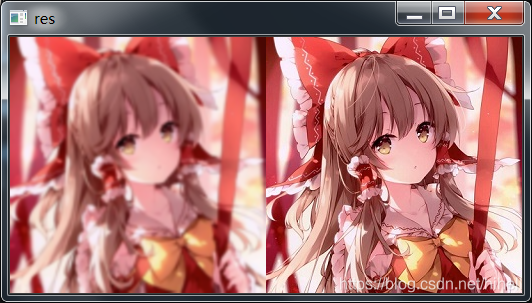
4、结果如图所示
(1)高斯金字塔

(2)拉普拉斯金字塔

注:拉普拉斯金字塔与《图像工程》(第4版)中的效果图不太一样,差别的源头可能出在原始图像“lena.png”的数据上!