一、构建方法

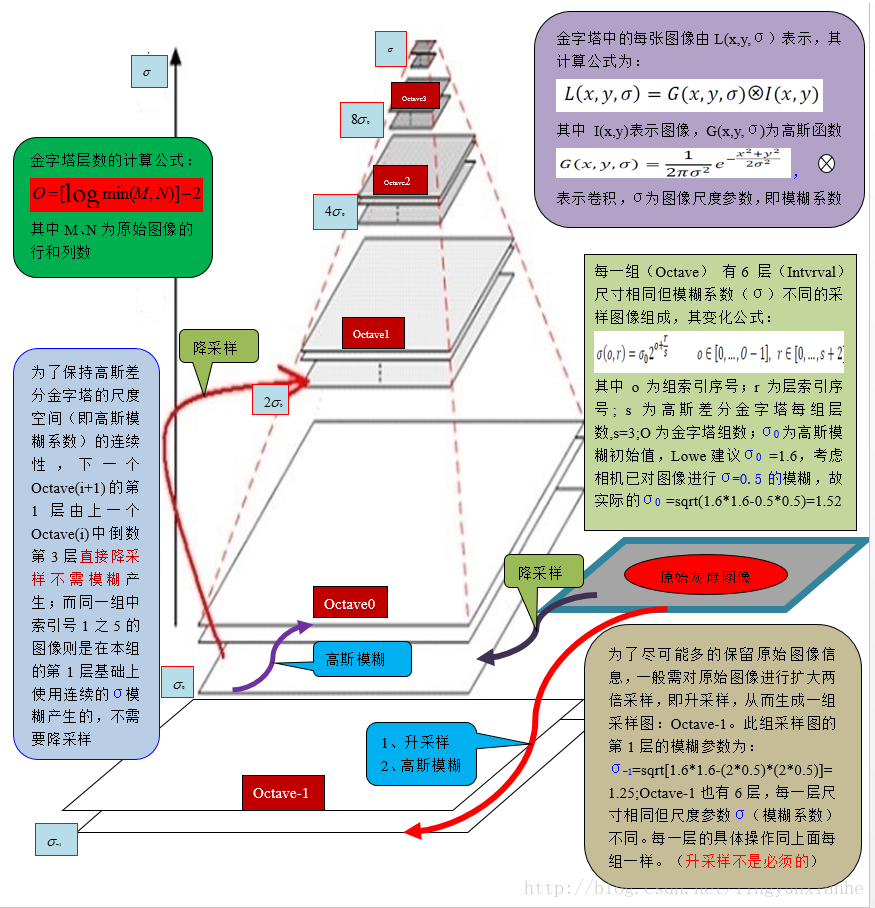
高斯金字塔每层图像的尺度为： $\sigma =\sigma_{0}2^{o+\frac{layer}{S}}$ 。理论上金字塔每层图像可以从原图做 $\sigma$ 的高斯滤波得到。但是实际操作中，每组的第一张影像（除第一组）是上一组倒数第三张影像降采样得到，其他影像是对前一张图像做一定大小的高斯滤波得到，而不是直接从原图获取。

因此，需要求取每组内影像间的高斯平滑尺度。假设前一张影像尺度为 $\sigma_{f}=\sigma_{0}2^{o+\frac{layer}{S}}$ ，那么下一张尺度应该为 $\sigma_{l}=\sigma_{0}2^{o+\frac{layer+1}{S}}$ 。 $\sigma_{l}$ 到 $\sigma_{f}$ 有公式： $\sigma_{diff}=\sqrt{\sigma_{l}^{2}-\sigma_{f}^2}$ 。 $\sigma_{diff}$ 即为从前一张图层到当前图层所需的高斯滤波尺度。 $\sigma_{l}$ 和 $\sigma_{f}$ 可根据金字塔层数求得。

对于每组的相同层影像，其 $\sigma_{diff}$ 相同。

二、函数重要点注释

void SIFT_Impl::buildGaussianPyramid( const Mat& base, std::vector<Mat>& pyr, int nOctaves ) const
{CV_TRACE_FUNCTION();/**    存储从前一张影像到当前影像所做的高斯滤波尺度，*    对于每一组，大小都一样*/  std::vector<double> sig(nOctaveLayers + 3);pyr.resize(nOctaves*(nOctaveLayers + 3));// precompute Gaussian sigmas using the following formula://  \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2sig[0] = sigma;double k = std::pow( 2., 1. / nOctaveLayers );for( int i = 1; i < nOctaveLayers + 3; i++ ){/**    sig_prev：前一张影像的空间尺度*    sig_total：当前影像的空间尺度*    sig[i]：前一张影像到当前影像，需要做的高斯滤波大小*/    double sig_prev = std::pow(k, (double)(i-1))*sigma;double sig_total = sig_prev*k;sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev);}/**    构建高斯金字塔*/for( int o = 0; o < nOctaves; o++ ){for( int i = 0; i < nOctaveLayers + 3; i++ ){Mat& dst = pyr[o*(nOctaveLayers + 3) + i];/**        如果是金字塔的第一张影像，*    使用图像预处理步骤获得的结果*        如或是其他组的第一张影像，*    使用上一组的倒数第三张影像降采样*        如果不是每组的第一张影像，*    进行高斯滤波*/if( o == 0  &&  i == 0 )dst = base;// base of new octave is halved image from end of previous octaveelse if( i == 0 ){const Mat& src = pyr[(o-1)*(nOctaveLayers + 3) + nOctaveLayers];resize(src, dst, Size(src.cols/2, src.rows/2),0, 0, INTER_NEAREST);}else{const Mat& src = pyr[o*(nOctaveLayers + 3) + i-1];GaussianBlur(src, dst, Size(), sig[i], sig[i]);}}}
}