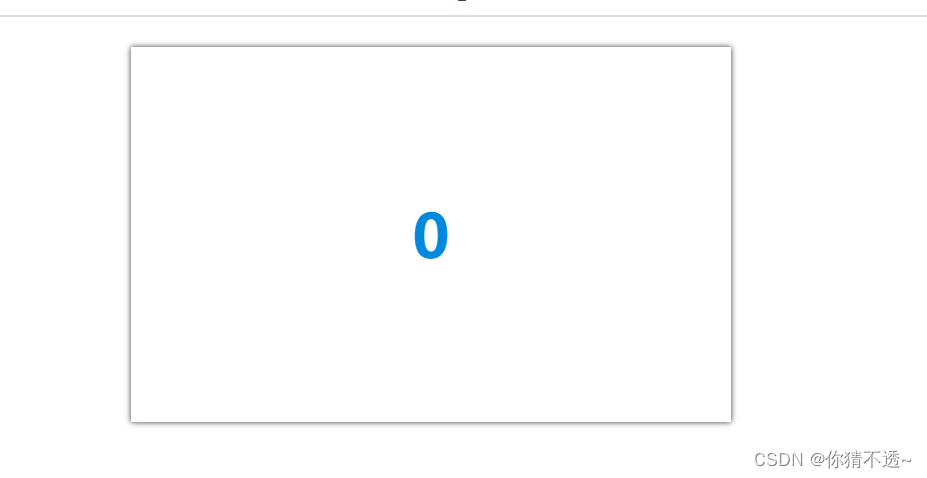
点积和叉积在计算机图形学的应用

点积和叉积在计算机图形学中，是最为基础且重要的概念，初学者弄清它的概念的应用，是很重要的。最后一节，是为了加强理解记录，如果不看也是可以的，大家选择观看，有兴趣可以去看原视频，结合我的笔记。

前置知识

列向量
以下均采用列向量的表示方法，和线性代数书本上的行向量不同，采用列向量表示，则表达为列向量左乘矩阵，只是定义的不同，其他含义没有什么不同。列向量写法如下：
$\overrightarrow{a} = \left( \begin{gathered} \begin{matrix} x \\ y \\ z \end{matrix} \end{gathered} \right)$
单位化
将向量的各分量除以向量的模即得单位向量，单位指模为1的向量。
向量加减法的几何意义
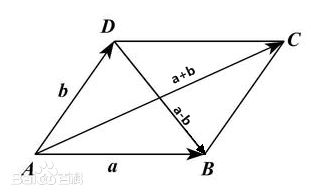
行列式
行列式在数学中，是一个函数，其定义域为det的矩阵A，取值为一个标量，写作det(A)或 | A | 。行列式可以看做是有向面积（二维）或体积（三维）的概念在一般的欧几里得空间中的推广。

点积

点积在数学中，又称数量积（dot product; scalar product），是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。点积的结果是一个数。

$\overrightarrow{a} \cdot \overrightarrow{b} = \left| a \right| \left| b \right| cos {\theta}$

相当于a向量的转置矩阵乘以向量b：
$\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{a}^T \overrightarrow{b}$

以二维向量为例：
$\overrightarrow{a} \cdot \overrightarrow{b} = {x_{a}\choose y_{a}}^T {x_{a}\choose y_{b}} = x_{a}x_{b} + y_{a}y_{b}$

在这里插入图片描述

几何意义

在这里插入图片描述
a向量在b向量上投影的长度乘以 b向量的长度（模）就是点积的结果。
点乘是存在交换律的，所以也等同于：
b向量在a向量上投影的长度乘以 a向量的长度就是点积的结果。

在图形学的应用

求两个向量的夹角
当 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 都是单位向量（单位化），两个向量点积就是 $\cos {\theta}$ ，在通过 $\arccos$ 就可以求出夹角。
求投影
将 $\overrightarrow{a}$ 单位化， $\overrightarrow{a} \cdot \overrightarrow{b}$ 就是 $\overrightarrow{b}$ 在 $\overrightarrow{a}$ 上的投影长度。
《计算机图形学》书上有这么一个举例，利用投影将向量w分解成两个向量和：
比较两个向量的接近程度（方向上）
也就是向量是否两个向量间的夹角大小，在聚光灯的效果计算中，可以根据点积来得到光照效果，如果点积越大，说明夹角越小，则物体离光照的轴线越近，光照越强。
也常会用来判断两向量是否为同方向：

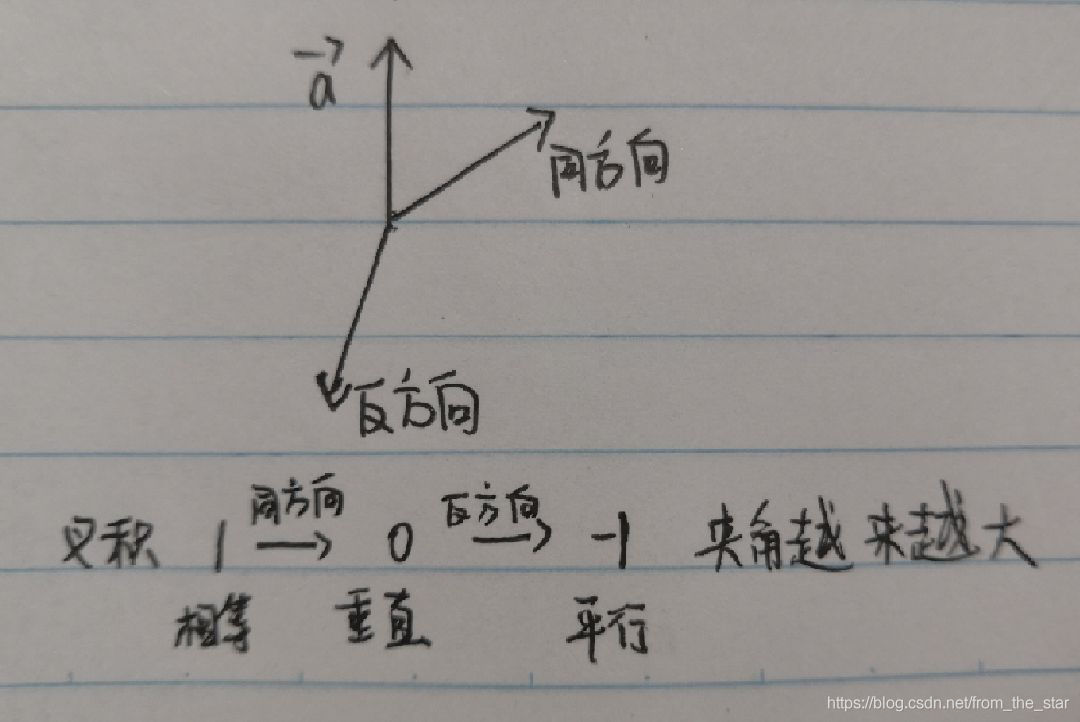
举个例子

判断一个点是都在某图形内：
在这里插入图片描述

叉积

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。
$\left| \overrightarrow{v} \times \overrightarrow{w} \right| = \left| v \right| \left| w \right| sin {\theta}$
这只确定了叉积的长度，众所周知向量有长度，还有方向的，方向为垂直于两个向量的方向，但是呢，垂直方向有两个。
这里我们采用右手螺旋定则确定方向。v到w的方向就是右手四指弯曲的方向，大拇指的方向就是叉积的方向。
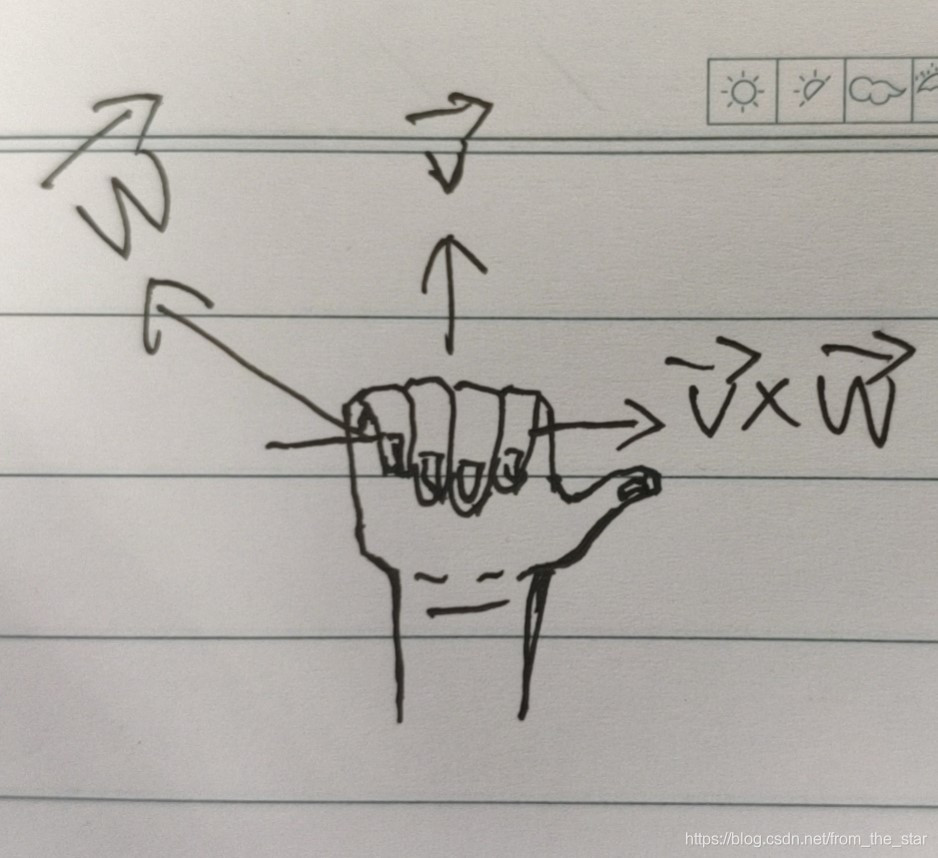
在这里插入图片描述

二维向量的叉积是个标量，看起来违背了定义，先假设二维向量得出来的叉积是z，如果把二维向量看作成z轴值恒为0的三维向量，它们的叉积就 $0,0,z)^T$ ，三维空间被压缩成了二维，叉积就只是一个标量了。

$\overrightarrow{v} \cdot \overrightarrow{w} = x_vy_w - y_vx_w$

三维向量的叉积的结果是个向量：

$\overrightarrow{v} \cdot \overrightarrow{w} = \left( \begin{gathered} \begin{matrix} y_v z_w - z_v y_w \\ z_vx_w - x_vz_w \\ x_vy_w - y_vx_w \end{matrix} \end{gathered} \right)$
这个看起来很难记忆，我们随后再讲解。444额方法
在这里插入图片描述

几何意义

在二维空间，两个向量叉积就是两向量形成的平行四边形的面积，正负要引入Z轴，由右手螺旋定则确定，如果大拇指指向Z正轴就为正，反之为负；
在三维空间，两个向量叉积就是垂直于两向量形成的平面的向量（称为法向量）采用右手螺旋定则确定方向。v到w的方向就是右手四指弯曲的方向，大拇指的方向就是叉积的方向。

坐标系的问题

如果我们已知x坐标轴和y坐标轴，可以推导出z坐标轴。可能大家都听说过有左手坐标系和右手坐标系这两种说法，可以用x、y轴叉积与z轴的关系确定。
右手坐标系：
$\overrightarrow{x} \times \overrightarrow{y} = \overrightarrow{z}$
左手坐标系：
$\overrightarrow{x} \times \overrightarrow{y} = -\overrightarrow{z}$

在图形学的应用

二维空间判断左右

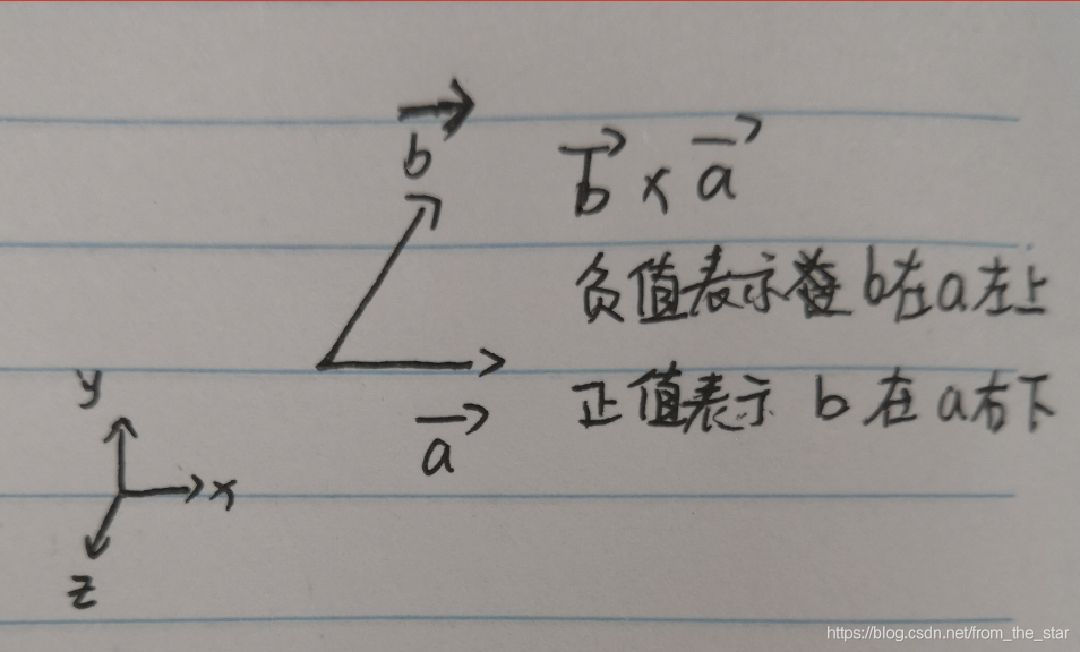
在这里插入图片描述
这个判断又可以衍生出如何判断一条路径存在交叉
2. 三维空间求法向量
法向量在计算图形学的应用很广泛，很多地方都会利用到，比如求已知入射角度 $\overrightarrow{OB}$ 求一个平面的反射角度 $\overrightarrow{BP}$ 。取平面上不共线的三个点ABC，求得法线
$\overrightarrow{AB} \times \overrightarrow{AC} = \overrightarrow{Z} （法线）$

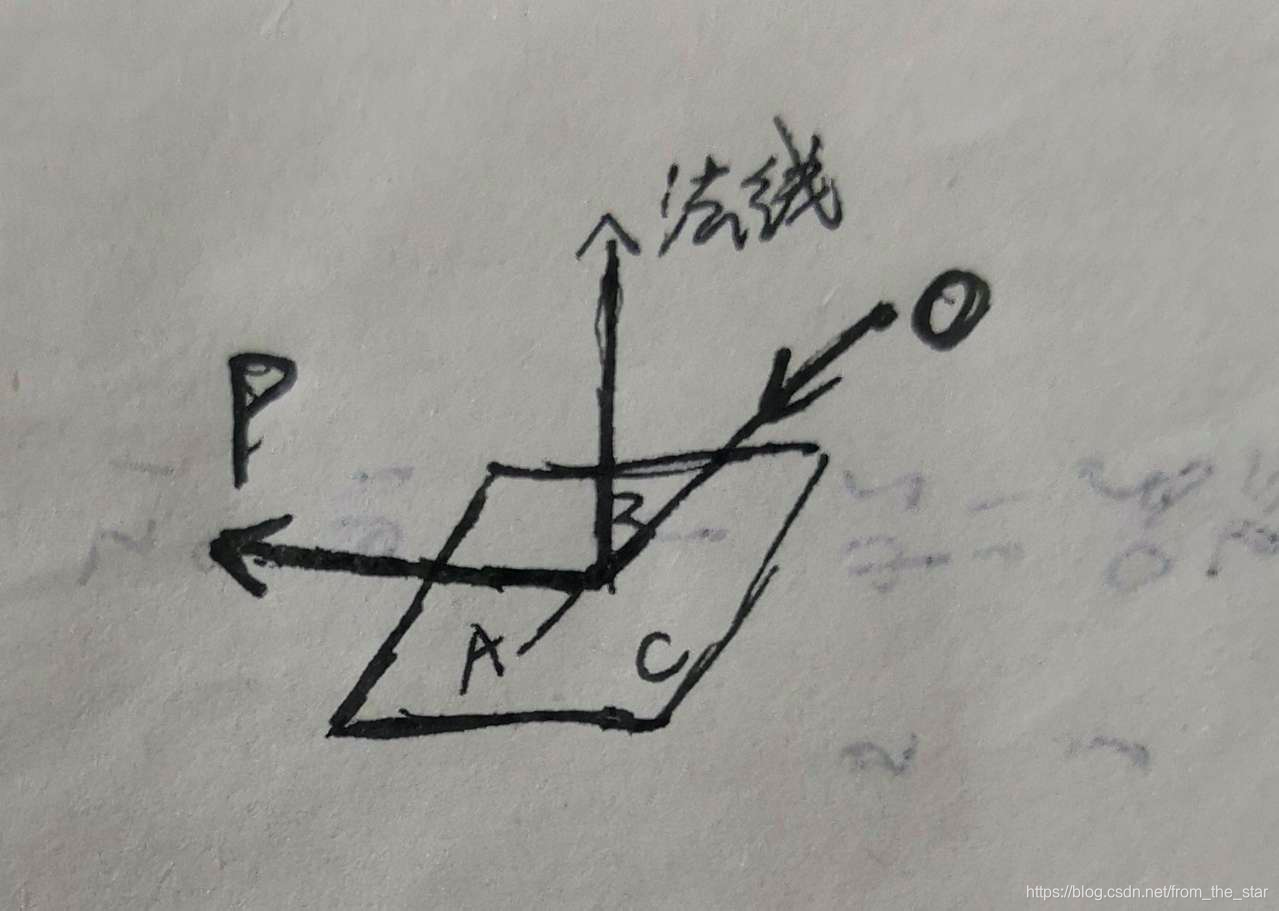在这里插入图片描述 $\overrightarrow{BP} = \overrightarrow{OB} - \overrightarrow{Z}$

再举个例子

判断一个点是都在某图形内
在这里插入图片描述

以线性变换去看点乘和叉乘

这部分我是基于B站的一部分的视频总结的，如果觉得作者讲解不够好，可以去看原视频。

点乘

先来看两向量的点乘另一种求法，a向量的转置矩阵乘以向量b：
$\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{a}^T \overrightarrow{b}$
以二维空间为例，定义两个基向量组成的矩阵
在这里插入图片描述
$\left( \begin{array}{c} 2 \\ 1 \end{array} \right)= 2\overrightarrow{i} + \overrightarrow{j}$
点乘就是从二维空间到数轴的线性变换，将空间投影到给定的数轴来定义。
$\overrightarrow{a}^T$ 矩阵作用就是，将基变量在 $\overrightarrow{a}$ 上投影为两个数字，而不是向量，将此作为基变量去做线性变换，从而进行空间压缩。

叉乘

截了视频的两张图，
在这里插入图片描述
$\left[ \begin{array}{c} x \\ y \\ z\end{array} \right]$ 表示一个随机变量，也可理解为一个为向量的变量。
上图是一个变量为向量的函数。根据v w 可以求常量 p

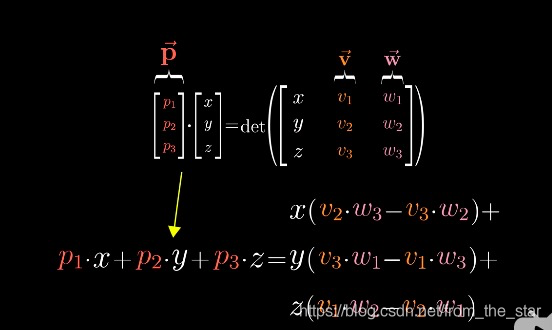
有没有觉得 $\overrightarrow{p}$ 与 $\overrightarrow{u} \times \overrightarrow{v}$ 叉积一模一样，那么我们认定 $\overrightarrow{p}$ 就是 $\overrightarrow{u} \times \overrightarrow{v}$ 的叉积，来解释叉积的几何意义。