前言：
本节，尝试通过线性变换来理解，或者说来表述点积。
在尝试理解的过程中，我们发现了线性变换，尤其是从多维空间到一维空间的线性变换，一定有某个严格的1x2的向量和他对应，这种微妙的而自然的联系，我们又将思路拓展到了更深入的模式，对偶。这节的内容比较难，但是，一旦理解，会讲你的数学思维水平提高一个新的层次，去理解向量，他无非是一个记号，一个表征变换的记号。而这种记号，我们再中间一下，就是一个对偶的特征再现而已。
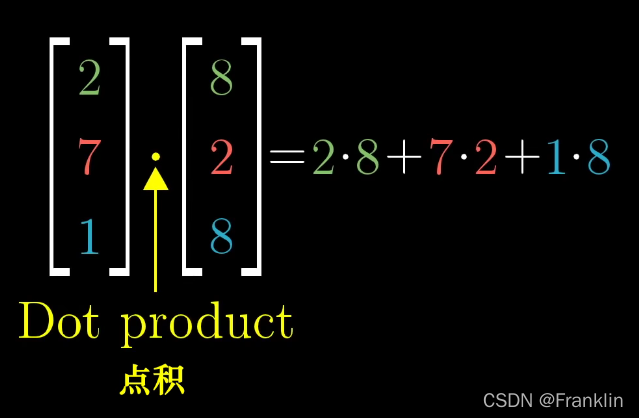
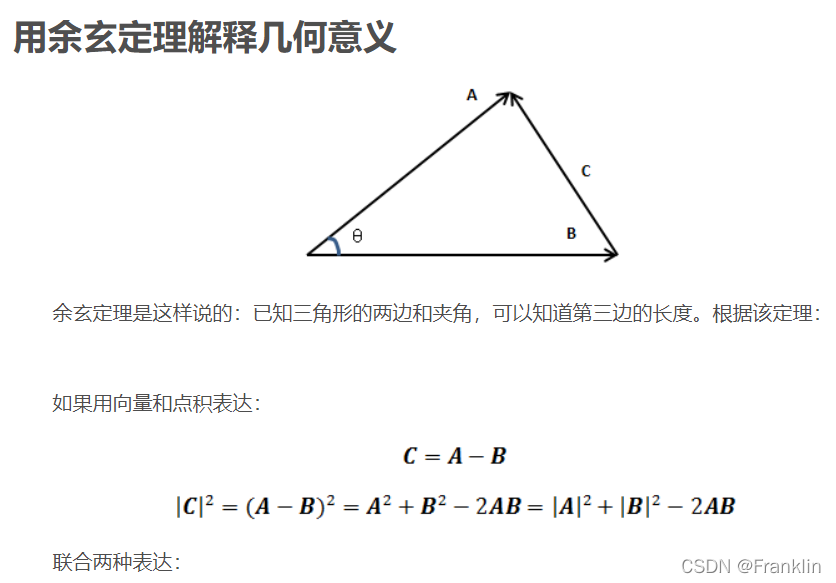
1 点积的通用定义和几何意义：
点积的几何意义：
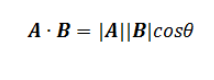
2 点积的计算定义：
【弹幕：点积，内积，点乘，标量积】
【点积应该看夹角，夹角为0，点积为零】
【夹角考虑余弦定理 】
3 点积几何意义的细说：
3.1 先投影
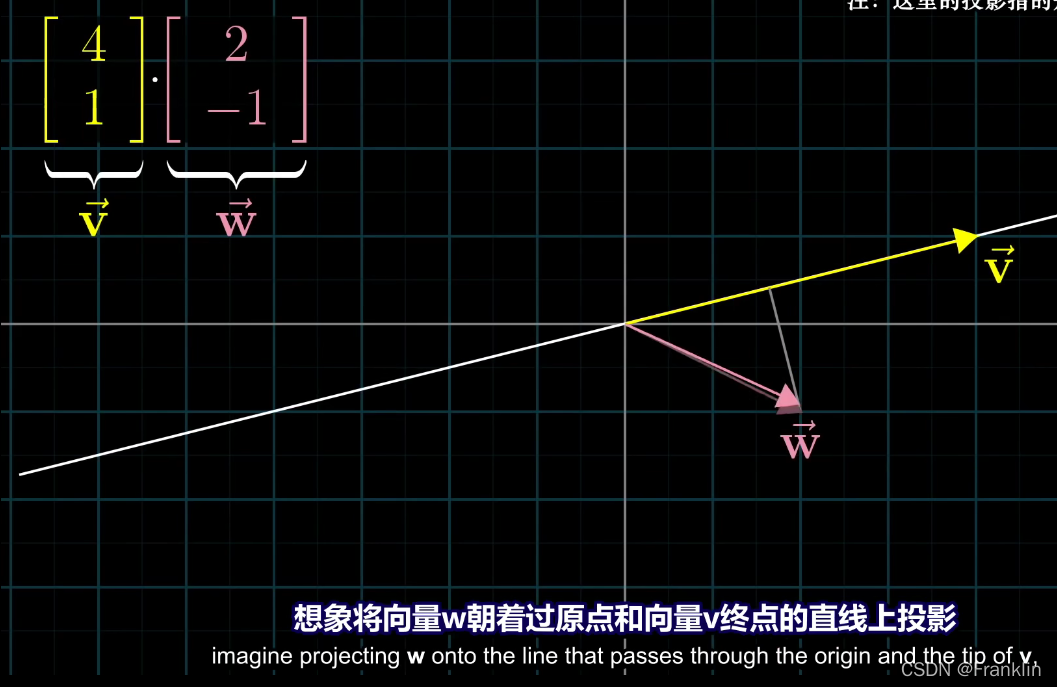
3.2 然后计算长度：
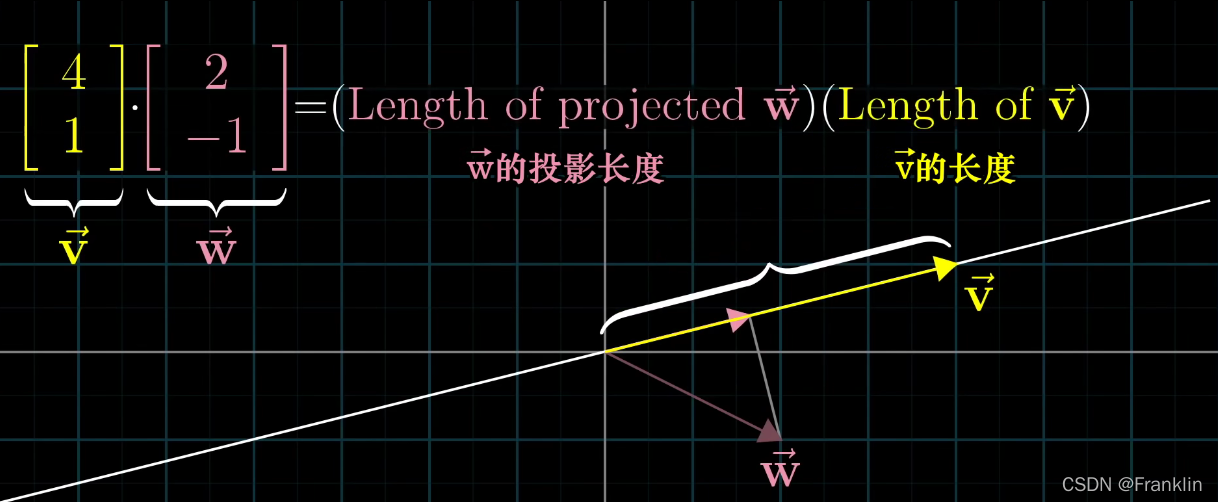
把w投射到v所在的直线上，将w在v上投影的长度乘以v的长度，就是其点积的值
【案，正交坐标系，加这句是因为向量的长度，如果是纯长度的话是没有考虑夹角的，我们必须考虑余弦定理的夹角啊】
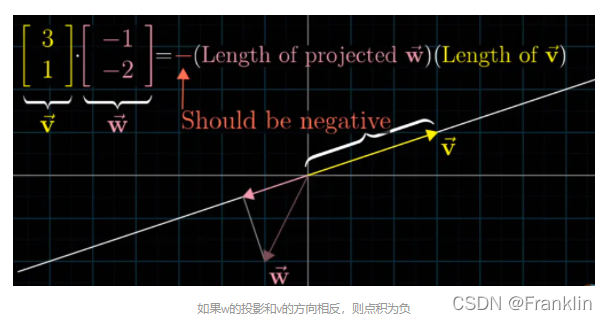
【案，线性代数的本质，这一节，我觉得有点太啰嗦，写的太细致以至于几乎没有耐心去看了，还是给出几个例子，把这个视频里面讲的知识应用一下：】
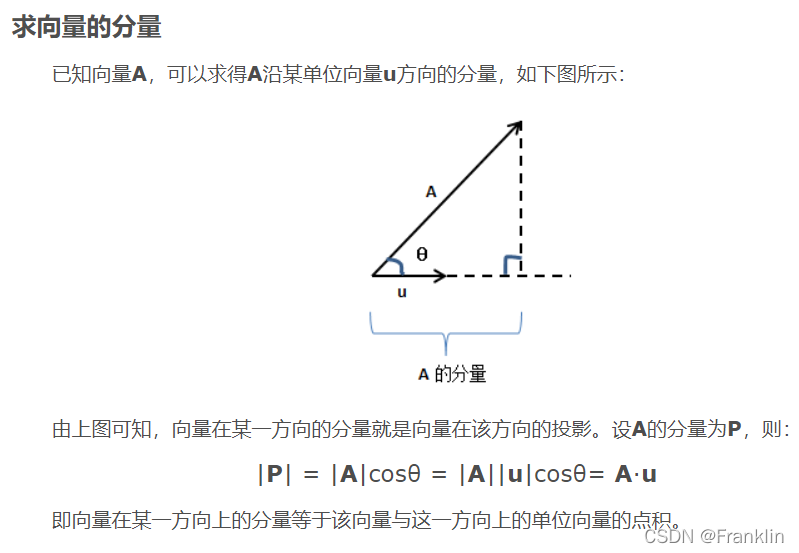
【案，投影和方向，其实就是余弦定理的应用，所以点乘的结果是向量的长度*向量的余弦值，而不是仅仅长度相乘，这一点视频估计有错误，或者忘了说了】
3.3 点积表述向量的关系：
＞0为向量方向相同：
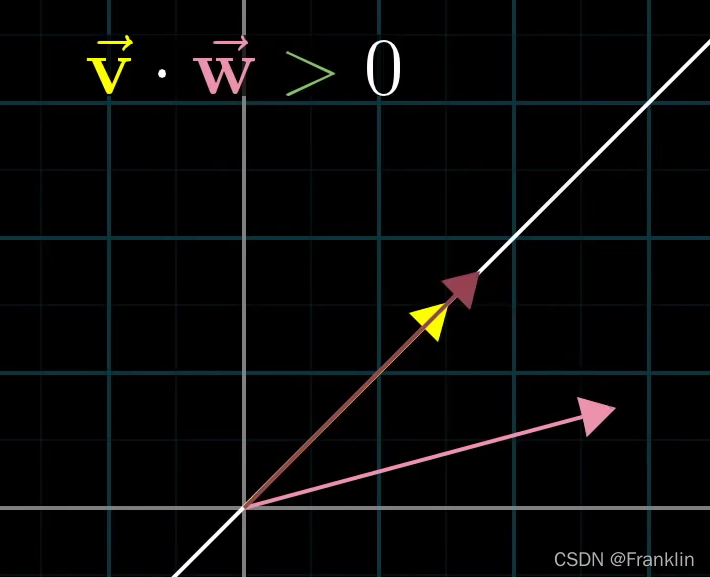
=0，向量在另外一个向量上的投影为0，cos90 =0
【案，又叫做正交性，看个例子】
【案，上面这个例子，计算了一个平面表达式的正交性】
<0
【弹幕】其实是余弦定理？
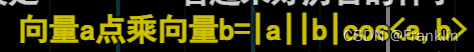
4 点积的性质：
4.1 和顺序无关性：
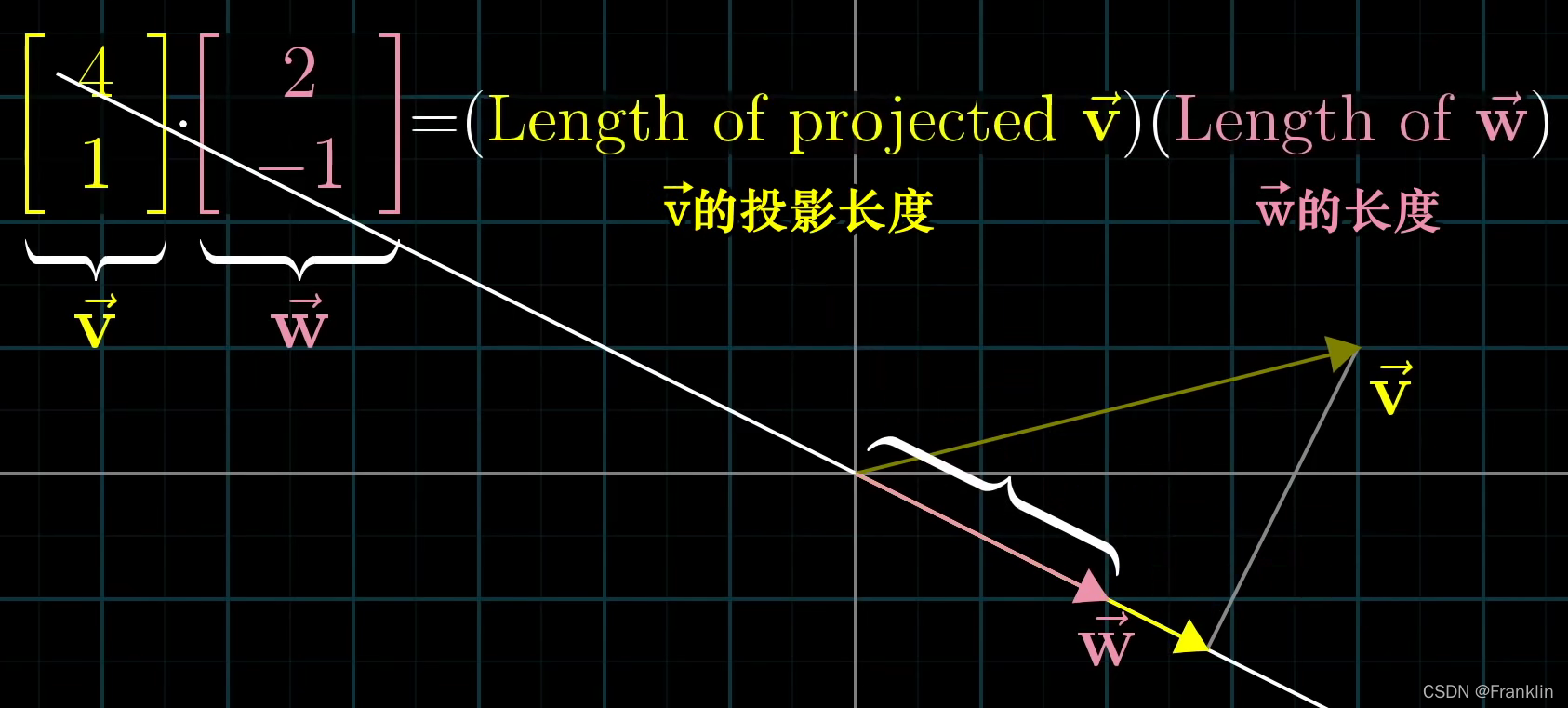
你可以w投射到v，或者v投射到w
【问题1】，为啥和顺序无关：
1 假设w，v相同
因为，w,v长度相同，那么我们可以利用对称性：
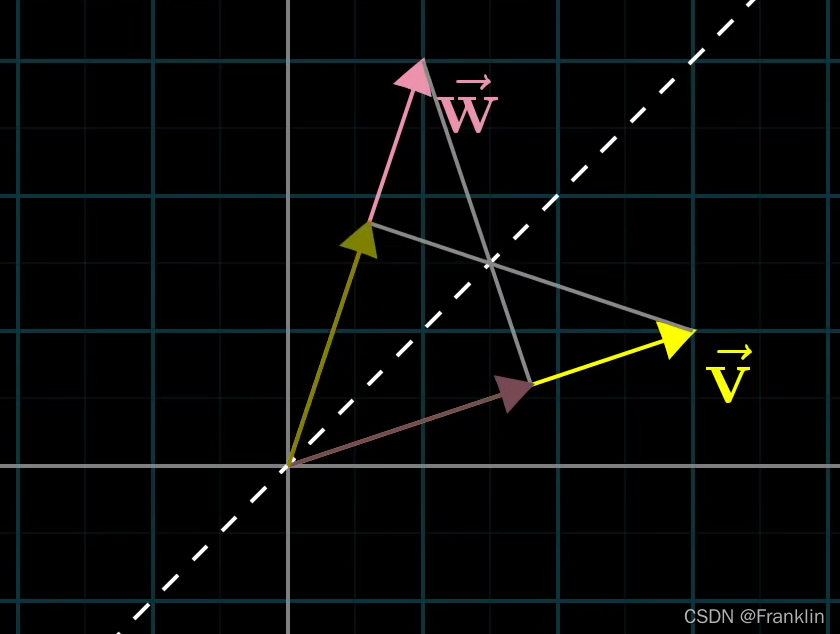
w,v互为镜像：这样应该没问题
2 现在拓展一下，如果v的长和w不同，
例如是2倍，
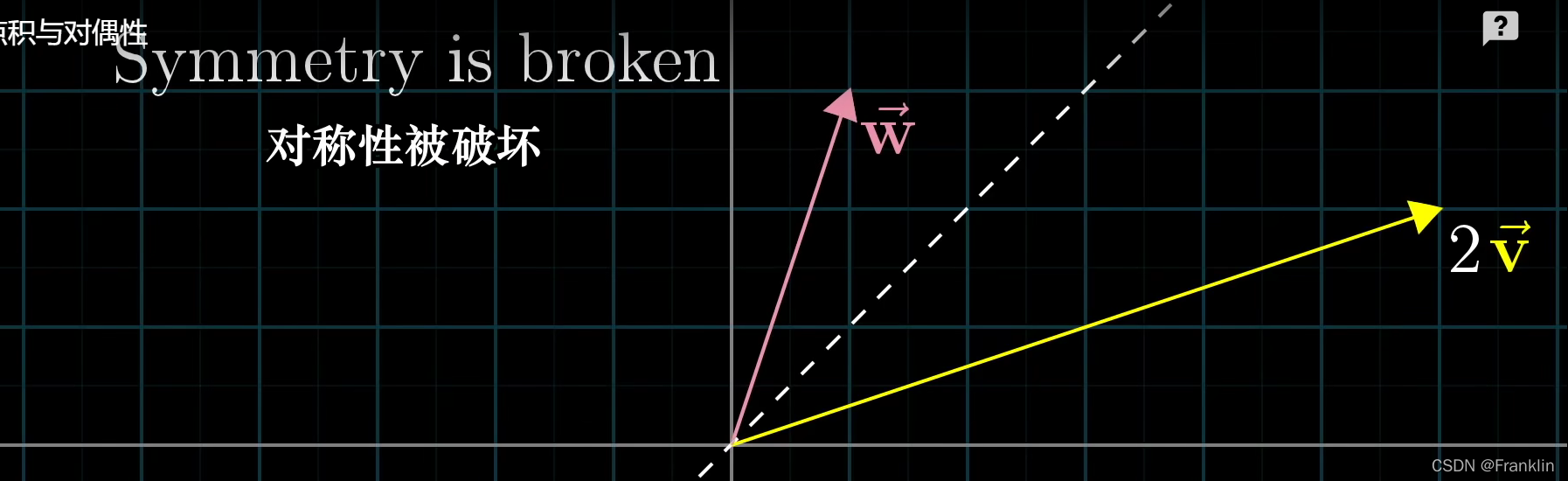
但是，我们可以理解为，w投射和v投射后，再搞翻倍的动作。因为，不管V怎么变化，他就是变成外星人，老实的w是没有变化的。
【弹幕】
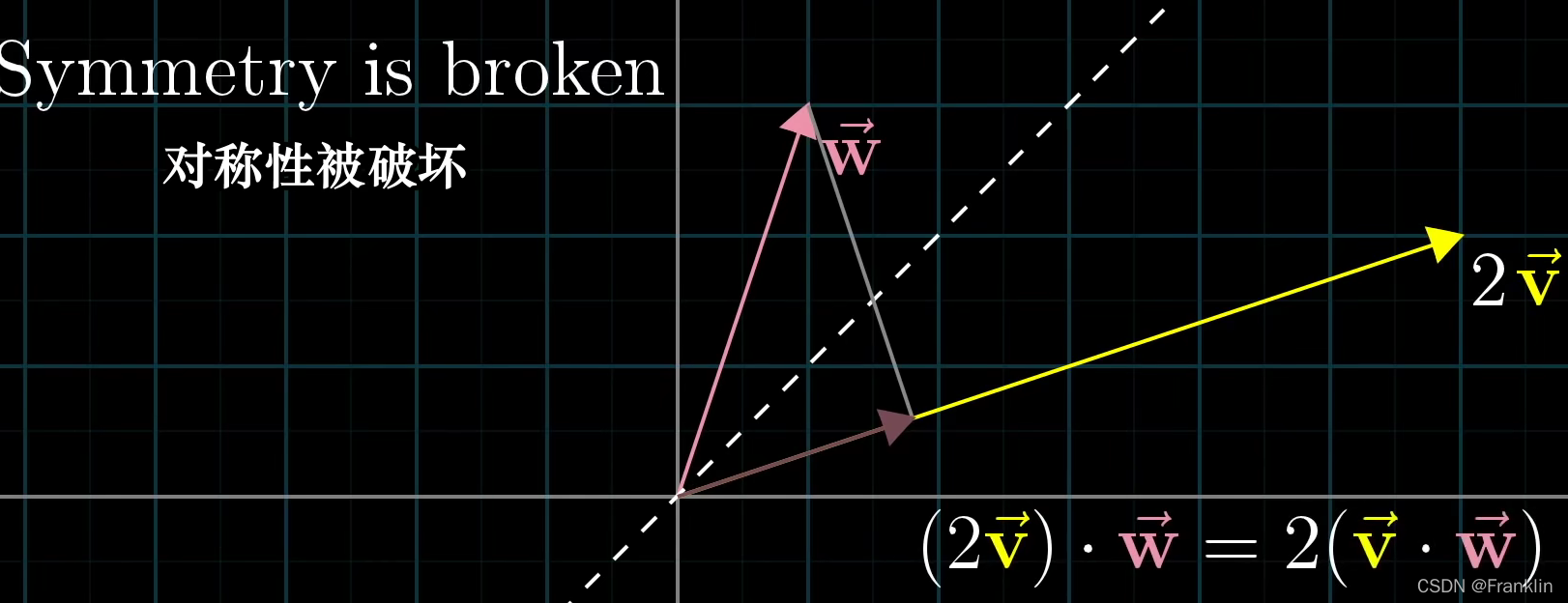
【案，是对偶的，可以反着操作】 理解为，向量的操作，每个分向量是独立的，或者理解为互为映射的，或者理解为乘法嘛。所以没有顺序。所以，这个顺序问题解决了。
问题2，为啥点积和投影有联系：？
下面用对偶性进行解释，考虑对偶之前，我们从下面多维到一维度空间变化开始搞事情。
5 点积和对偶性：
这节，解释点积和空间的投影的对应建立的关系理由。
5.1 多维空间到一维空间的转换：
数轴上的两个向量，为一维空间：
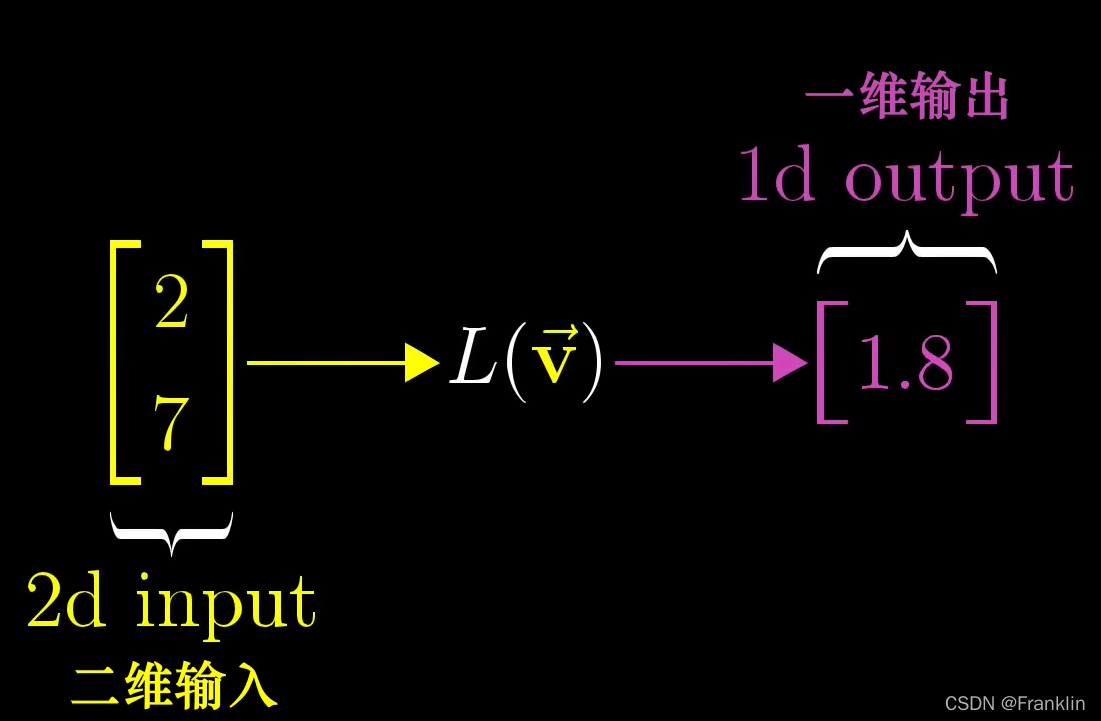
我们简单的用等距离的点来表示线性空间
现在，我们看，在数轴上基向量就是两个数字：
这是个1x2的矩阵：
6 我们再考察一个例子：
将待变换的基向量从二维的空间【4,3】T【列的元素2个】，
通过线性变换【1，-2】
会得到什么样的向量呢？
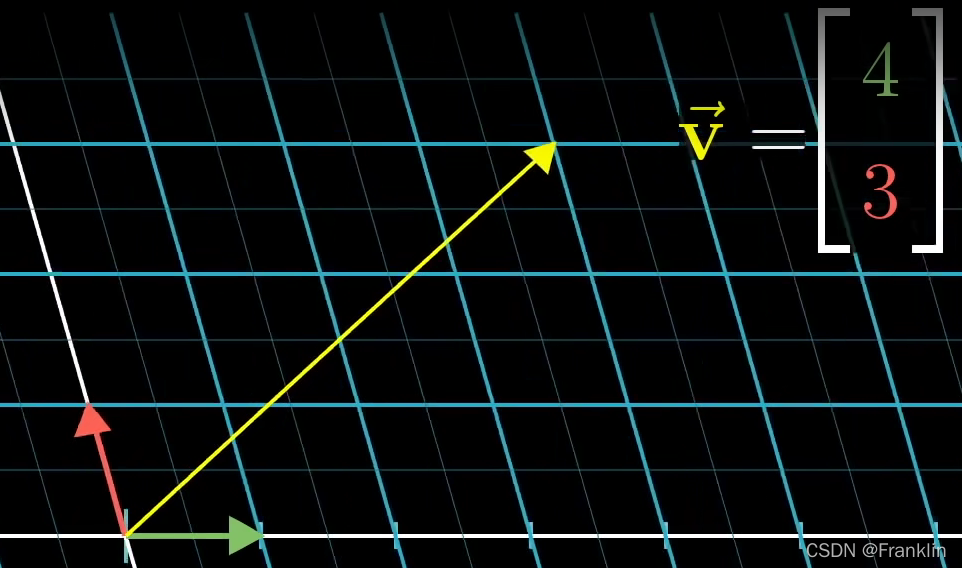
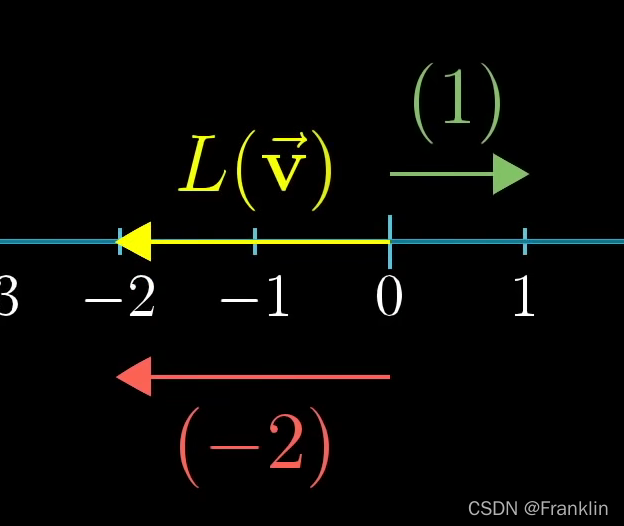
我们跟踪这个向量的变换，待变换的向量基向量分别乘以线性变换然后相加，
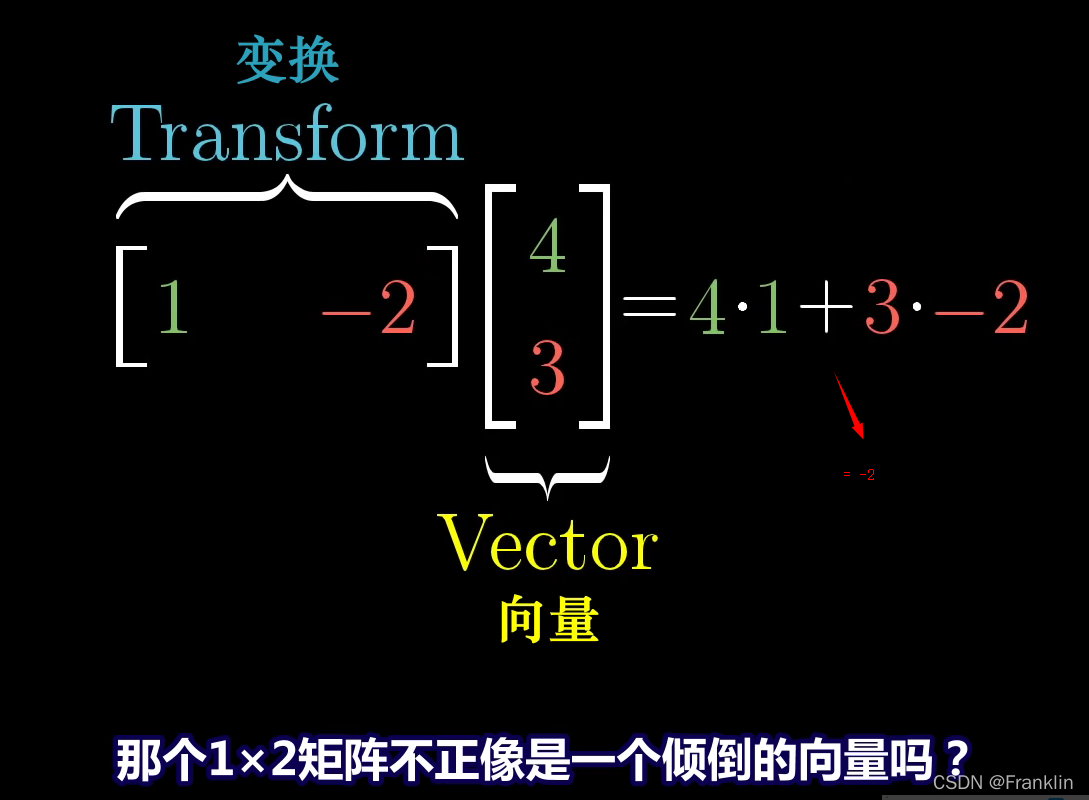
上面这个乘积的过程，其实就是很像点积的过程，只不过什么呢，
只不过我们把其中一个向量给倒了一下，就是行、列倒了一下。
【案，记住我们的想法是找到点积、对偶和向量空间的联系】
是时候我们开始公示【1x2矩阵和二维向量之间的微妙联系了】- 【先表述他们之间数值的关系】
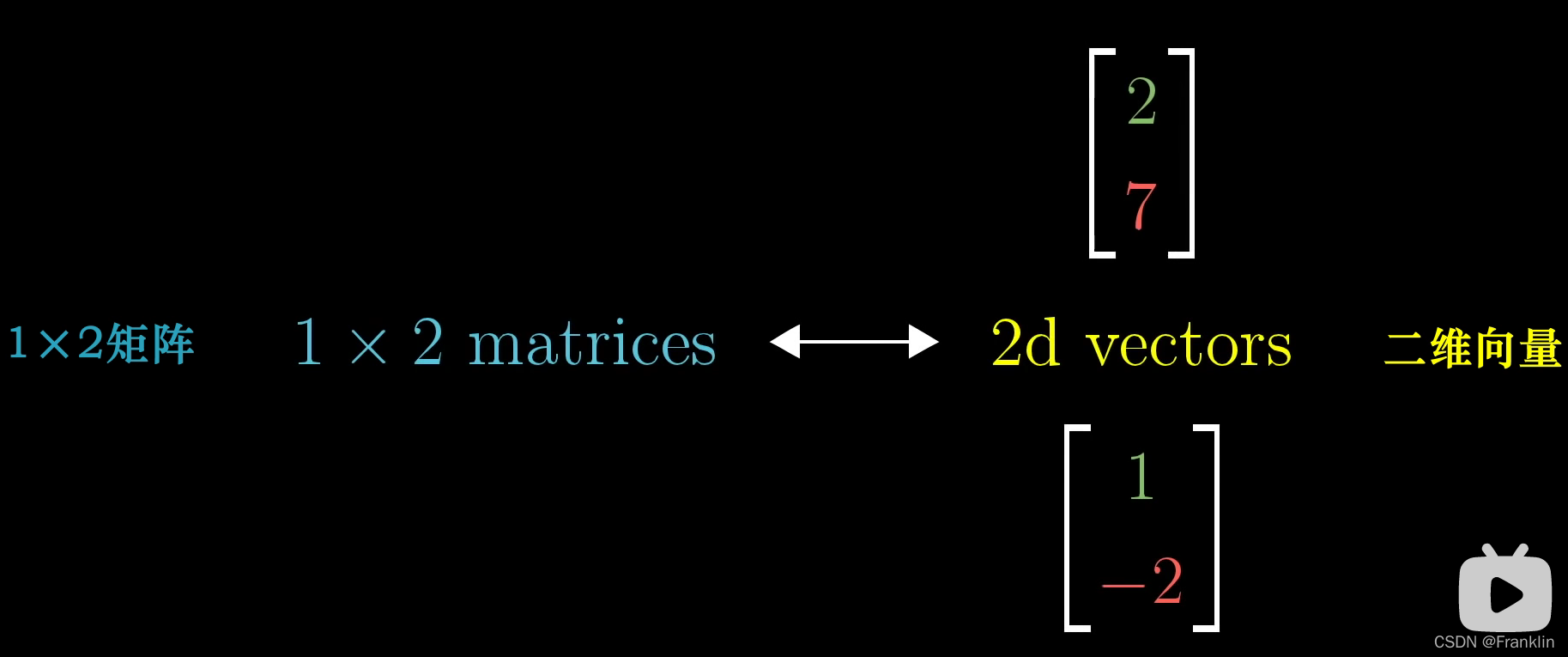
上面是一对二维向量
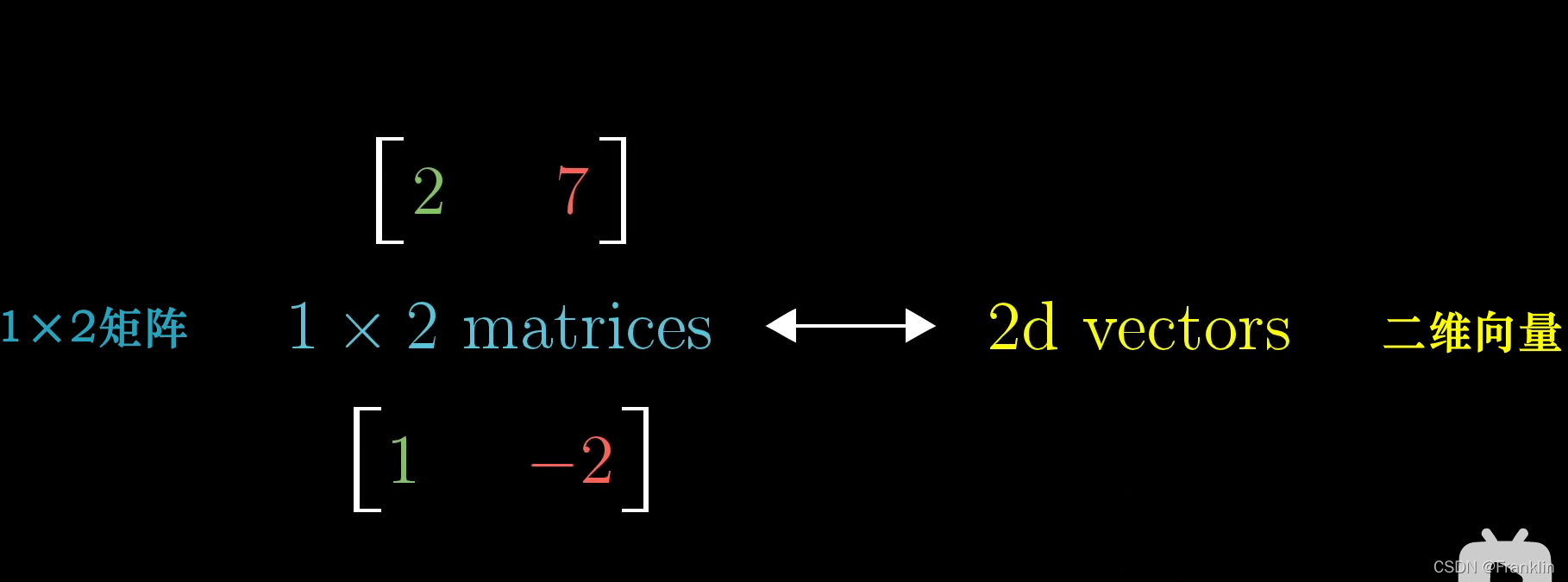
上面是一对1x2的矩阵
然后，我们看他们之间向量空间的几何关系，
1 构建一个斜向的数轴：
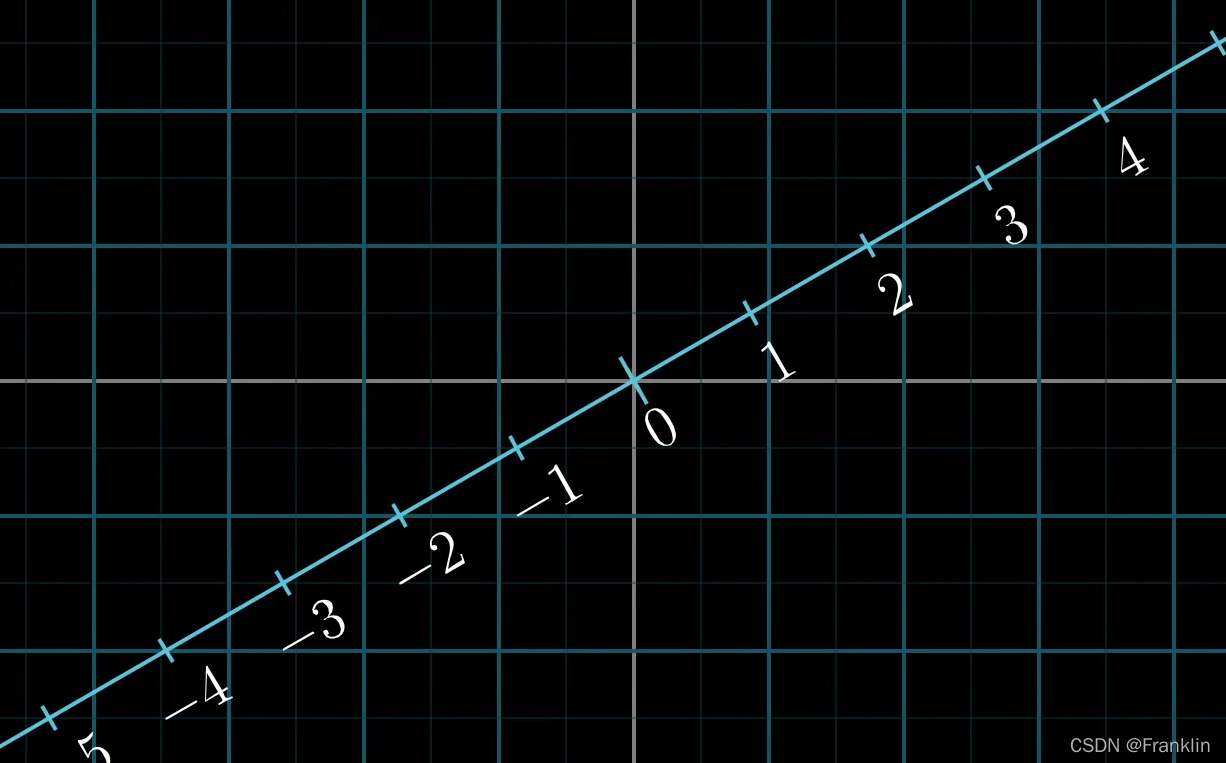
【案，这个数轴是在一个二维空间】
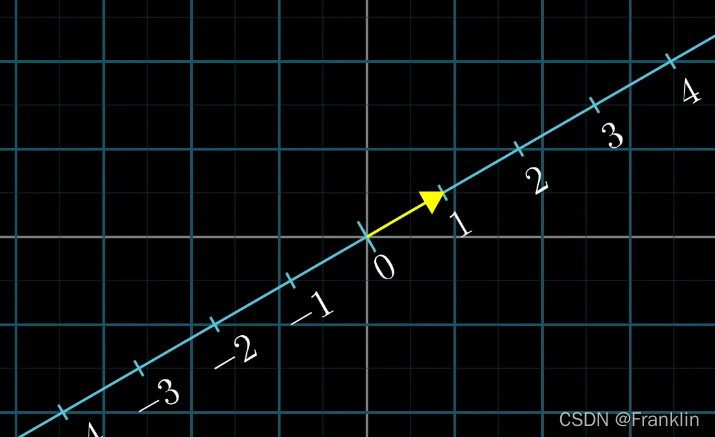
2 在这个数轴上，有一个二维向量U，终点落在这个数轴的1上。
【落在1上，考虑为单位向量】
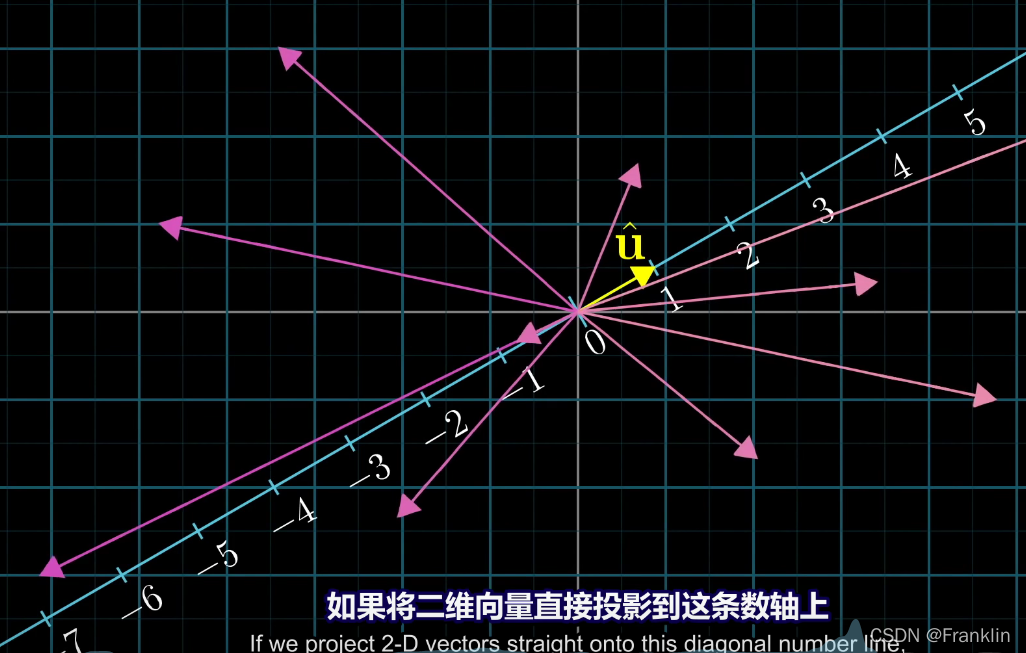
如果将二维向量直接投射到这个数轴上，前面我们已经讨论，我们只需要考虑向量的尖部tips,也就是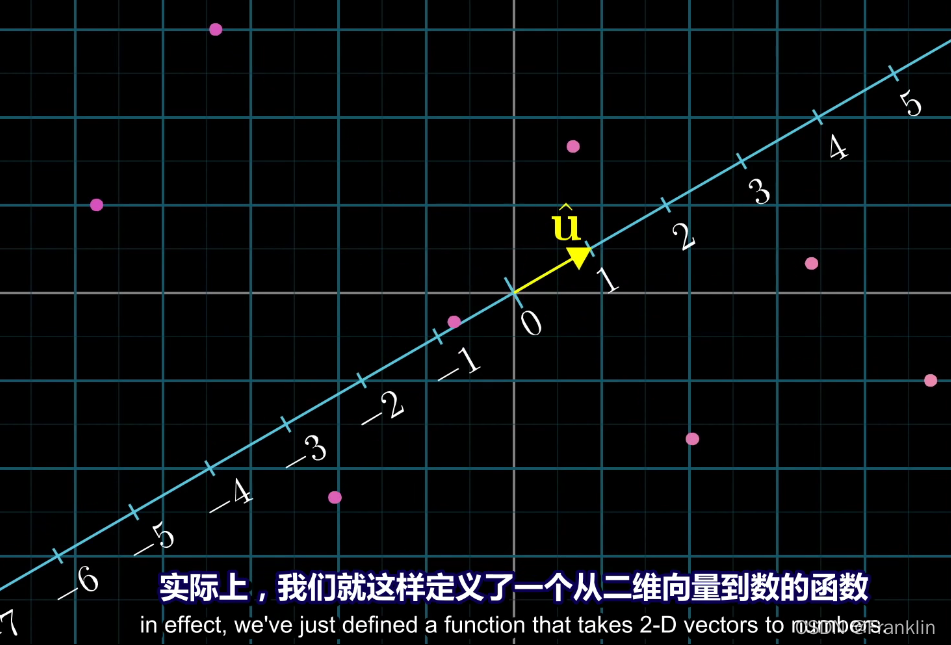
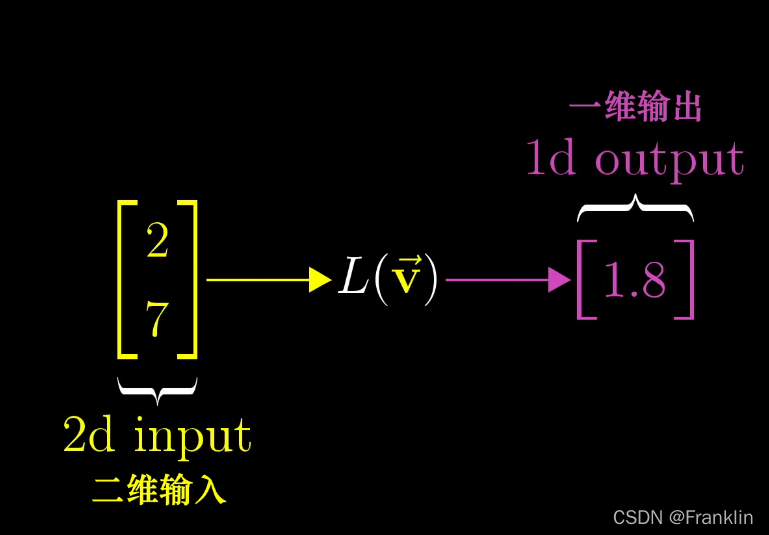
这样我们就构建了一个，二维向量到数轴上的数的一个映射，也就是函数。
【前面的章节我们提到过，这个对应关系其实是可以理解为函数，但是，因为向量有方向，所以，我们用变换来代替函数。但是，现在又是一个数了，这个映射可以再理解为函数】
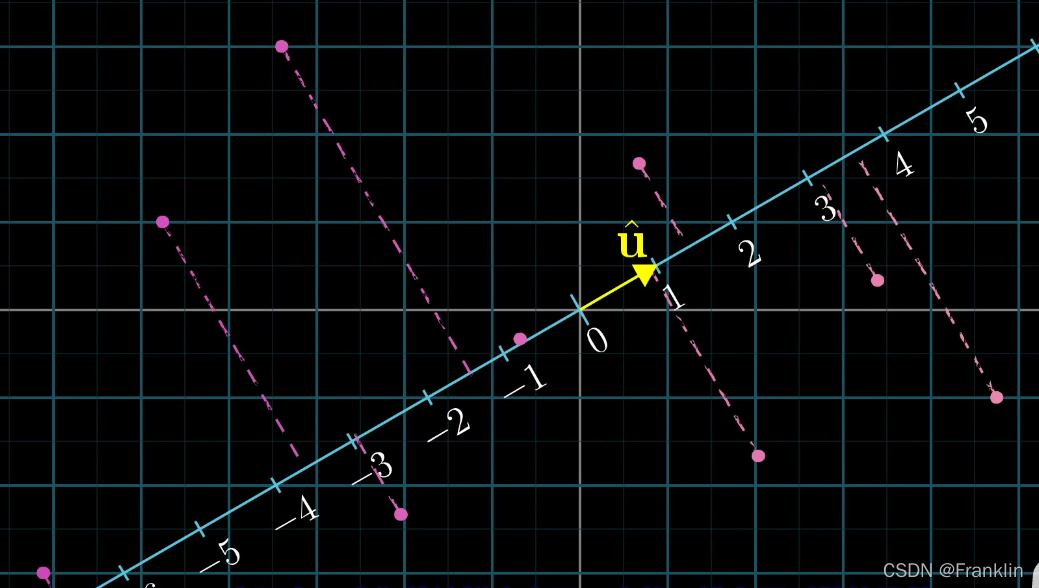
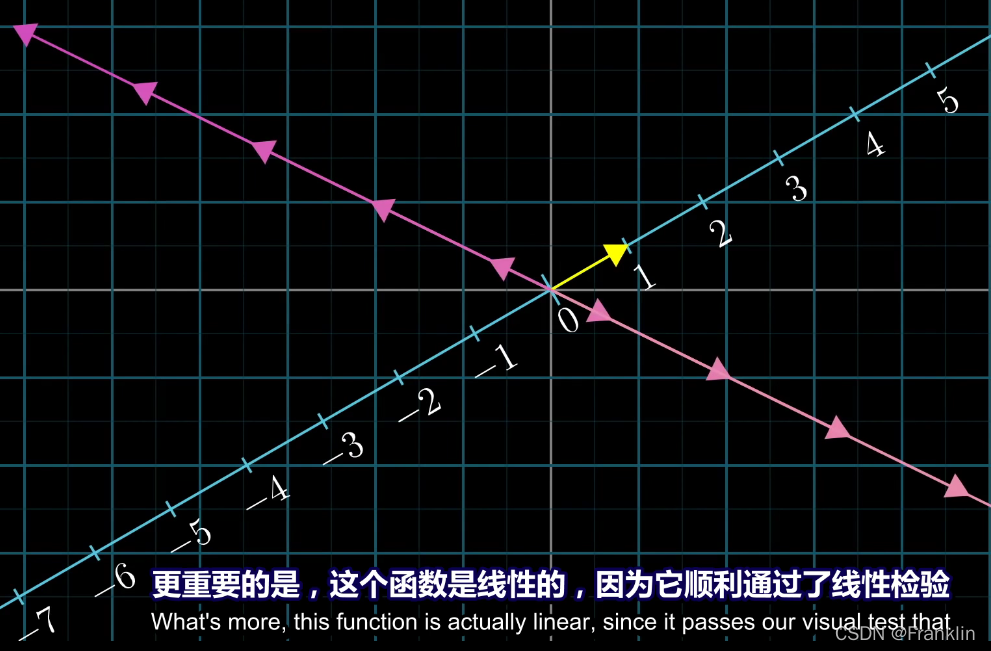
当然，这个函数是线性的，因为投射也是等距离的。
然而，我们刚才定义的U向量，是众多二维向量空间的一个向量，他正好和数轴重叠。
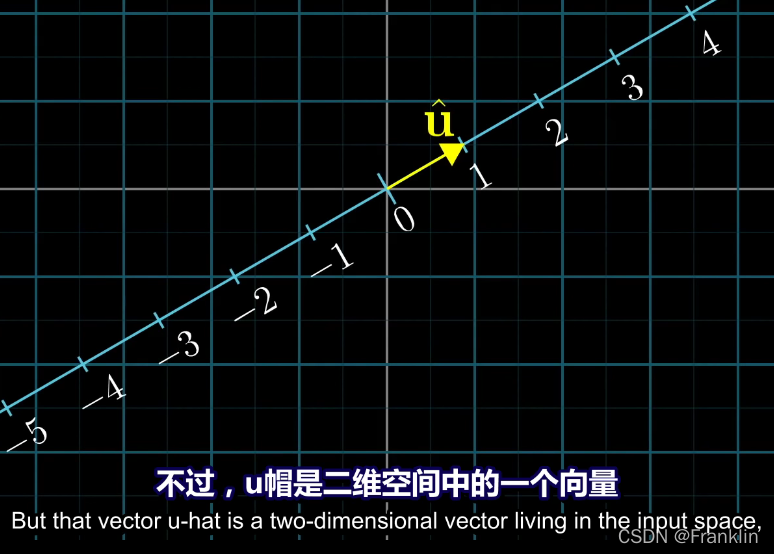
而这个投影，正是一个二维向量到数的一个线性变换。【注意，这里是一个数，而不是一个向量，这样后面的讨论就比较方便】
现在，我们来来尝试找到能够描述这个变换的1x2的矩阵，
为了找到这个变换的矩阵，
我们把这个斜着的数轴放大来看：
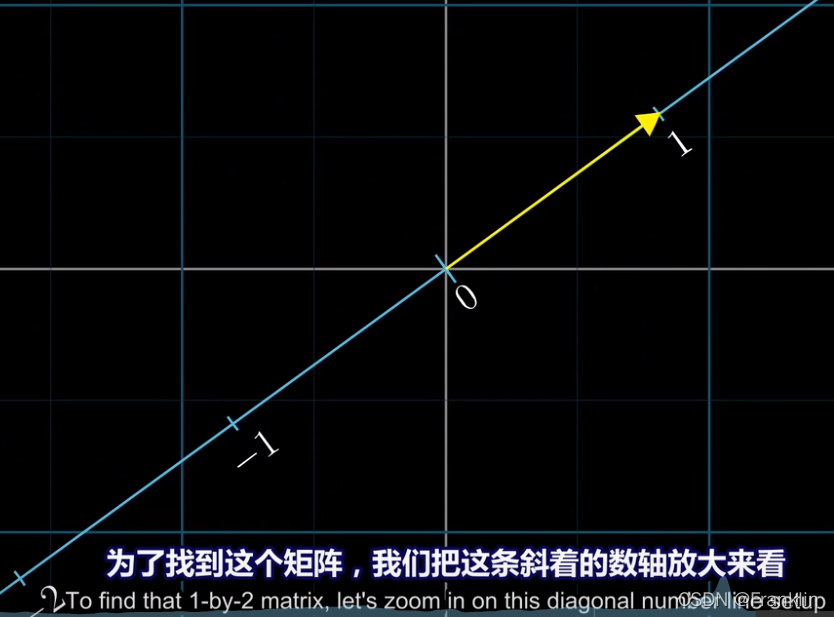
并且需要考虑变化后，基向量的位置【基向量就是要找的矩阵的列】
【以下部分非常精彩】
【通过精妙的对称性来进行推理】
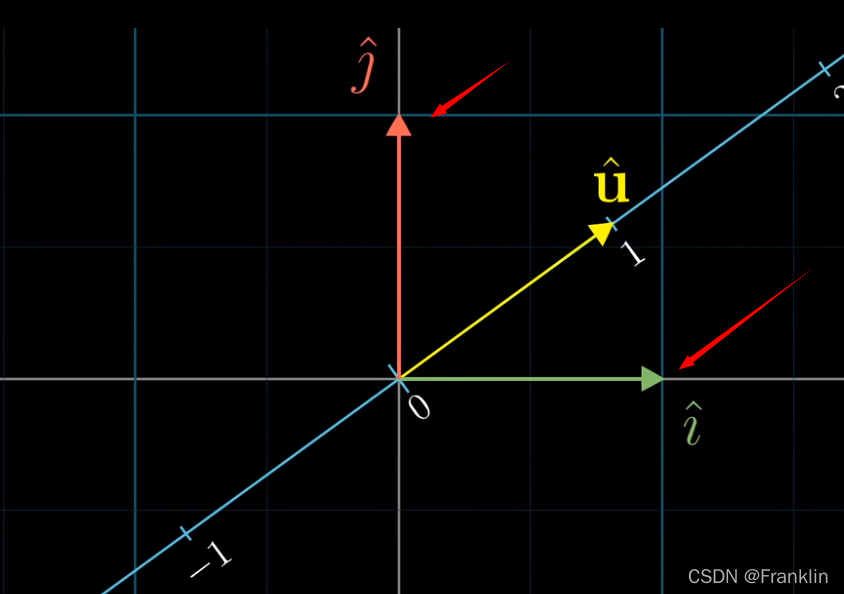
并且需要考虑变化后，基向量的位置【基向量就是要找的矩阵的列】
【^i】和【^u】都是单位向量，
由于U向量的特殊性，我们有，向量U投影就是向数轴投影。
【这一点其实前面已经讨论，再讨论一下】
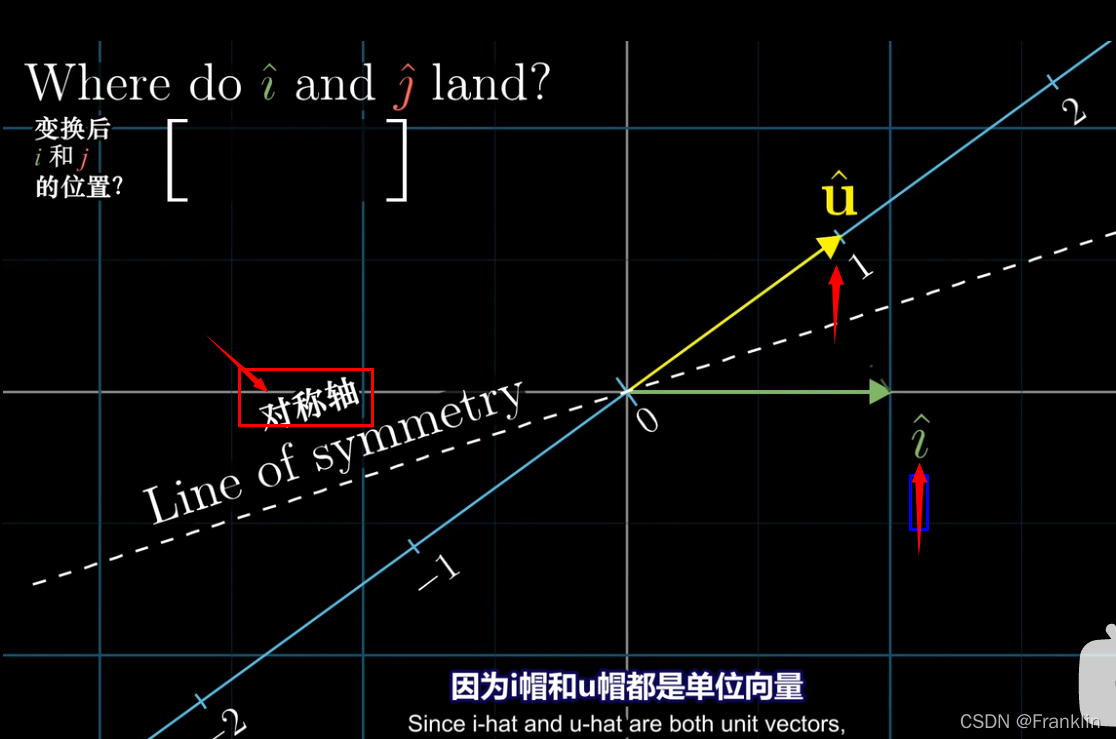
单位向量，那么长度一致，由于对称，所以，【^i】向【^u】的所在直线的投影和【^u】向【^i】的X轴的投影是对称的。
【所以，如果要问【^i】投影后落在这个斜向的数轴的哪个数上？
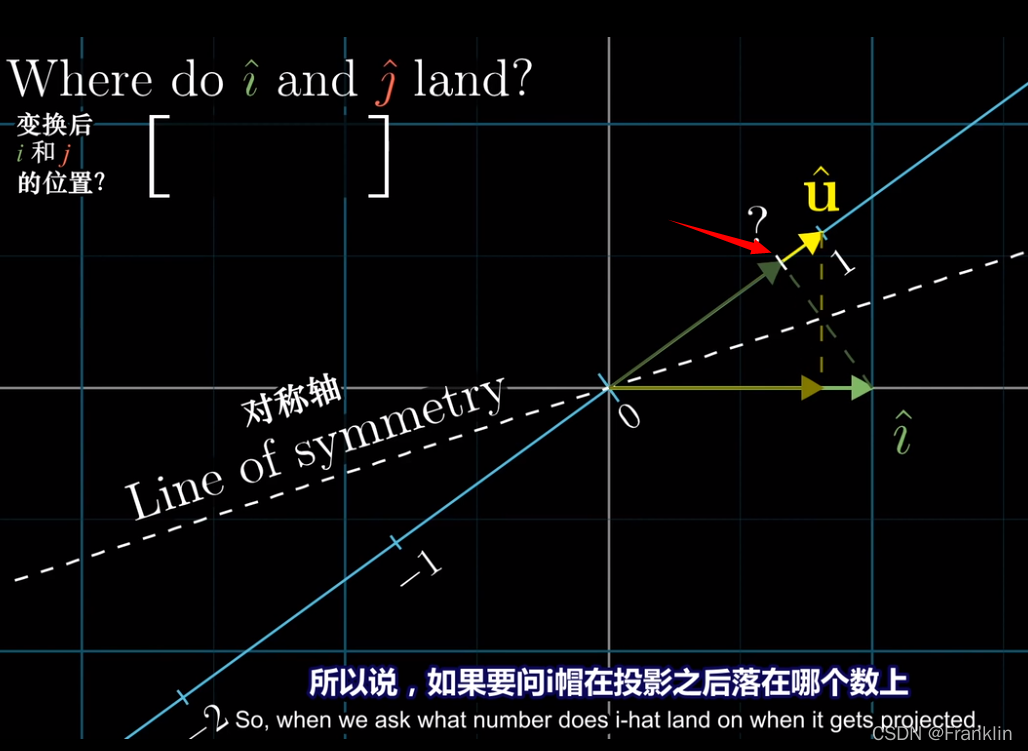
答案就是【^u】向X轴的对称投影所得的数。
而，
【^u】向X轴的投影，正是【^u】的横坐标，
也即是，
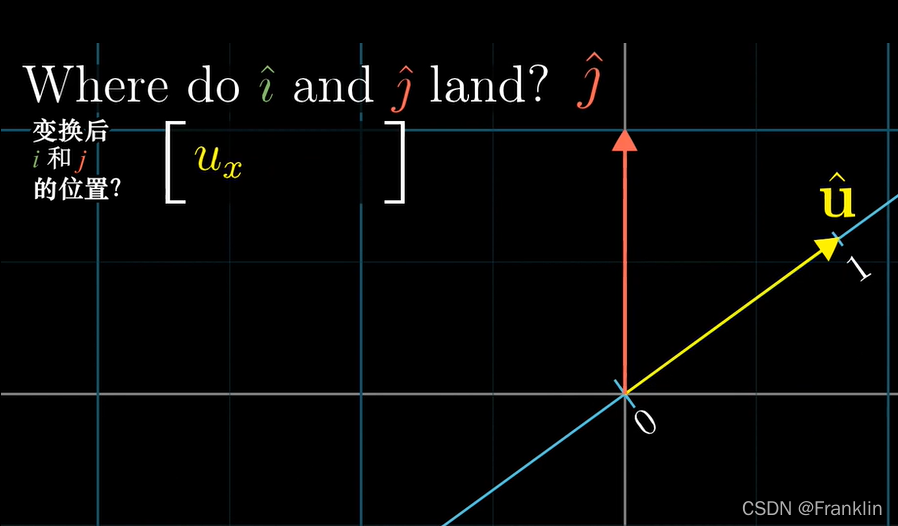
同理的【^j】的在斜向数轴投影后数，就是他的Y坐标。
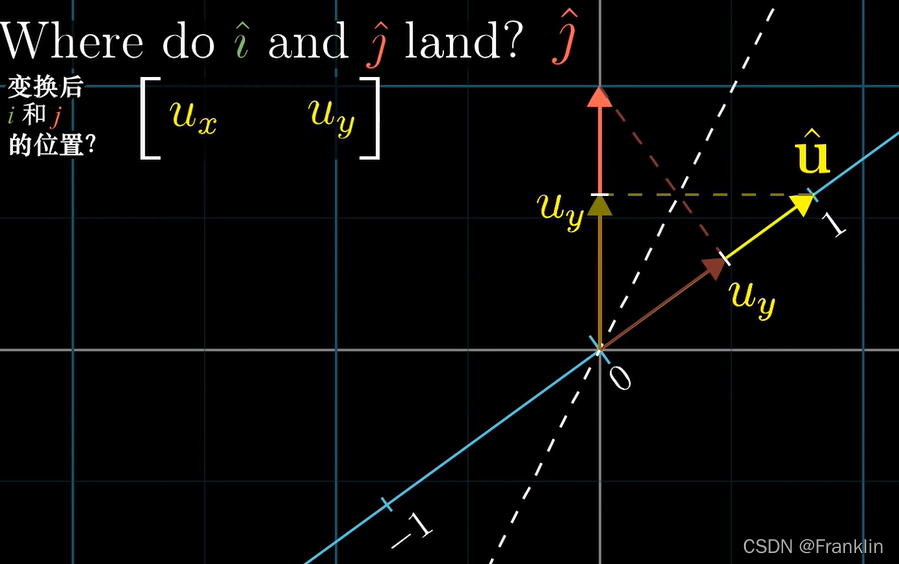
由此，并且需要考虑变化后，基向量的位置【基向量就是要找的矩阵的列】
所以，这个1x2矩阵【ux,uy】表述了一个二维向量【^u】到数的投影变换，而这个变换，的就是你要投影的基向量【^u】的两个坐标构成的。
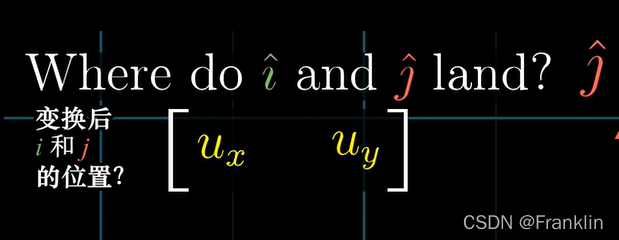
上面的例子，我们找到了一个单位向量u的投影变换【ux,uy】。
现在，
如果是整个二维空间的向量x,y，推而广之，就是
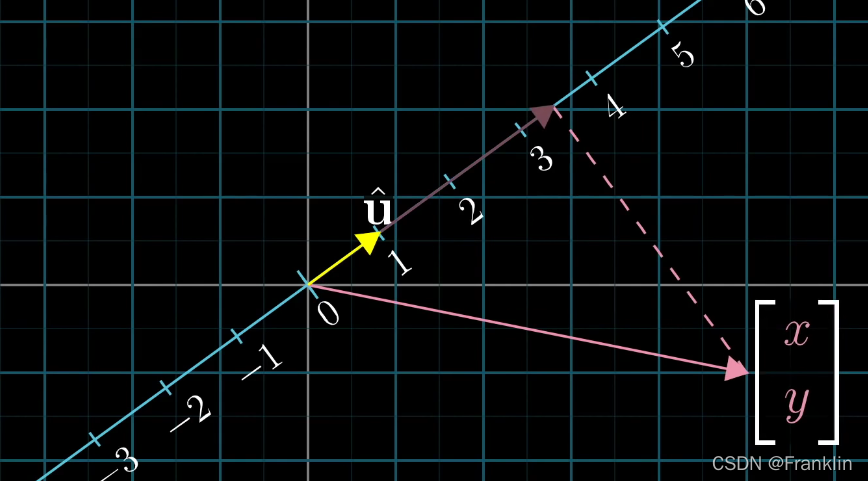
计算空间任意一个向量的投影变换，我们命名这个向量为【v】，
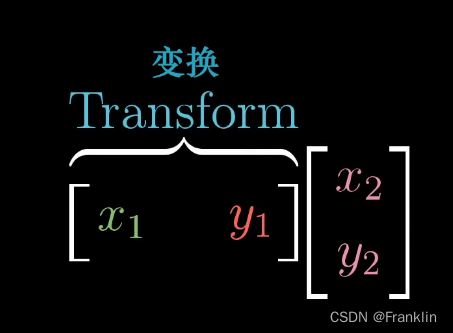
就是投影矩阵【Transform】和这个要变换的向量 v【x,y】的乘积。
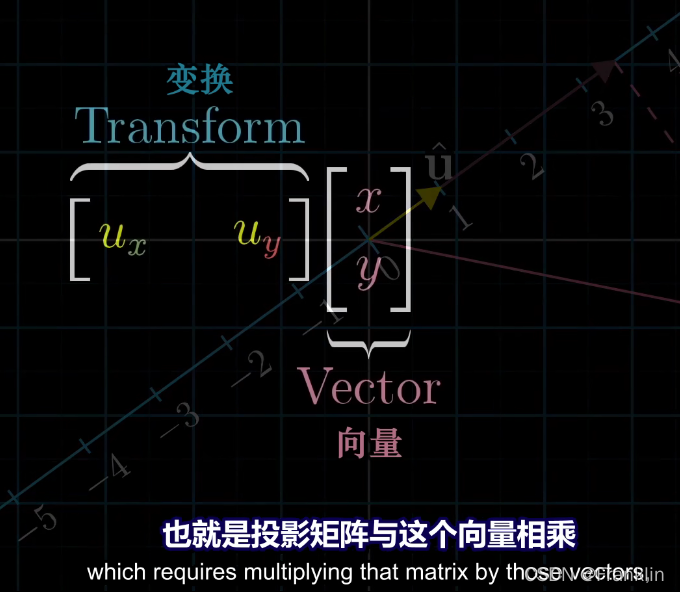
最后，我们得出结论：【微妙的联系】
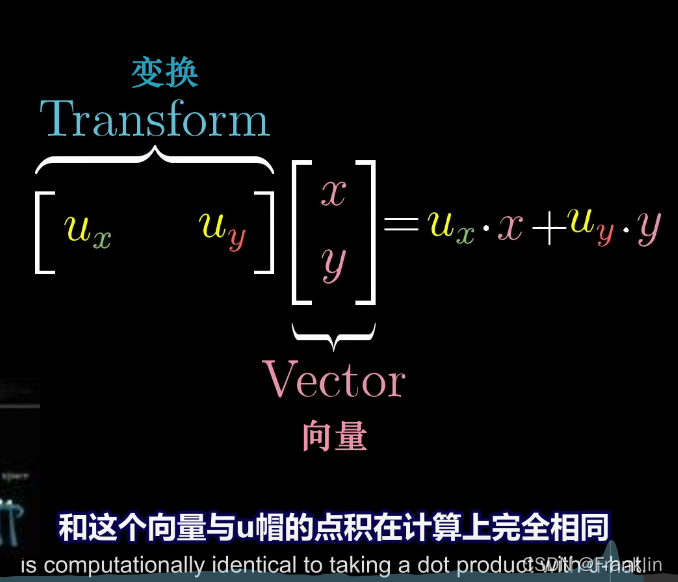
矩阵向量的乘积和点积之间的表达的关系，如下：
这就是为什么，与单位向量的点积，可以解读为 将向量【v】投影到单位向量【u】所张成的空间上（SPAN）【这个例子里是一条斜的数轴直线】，所得的投影的长度。
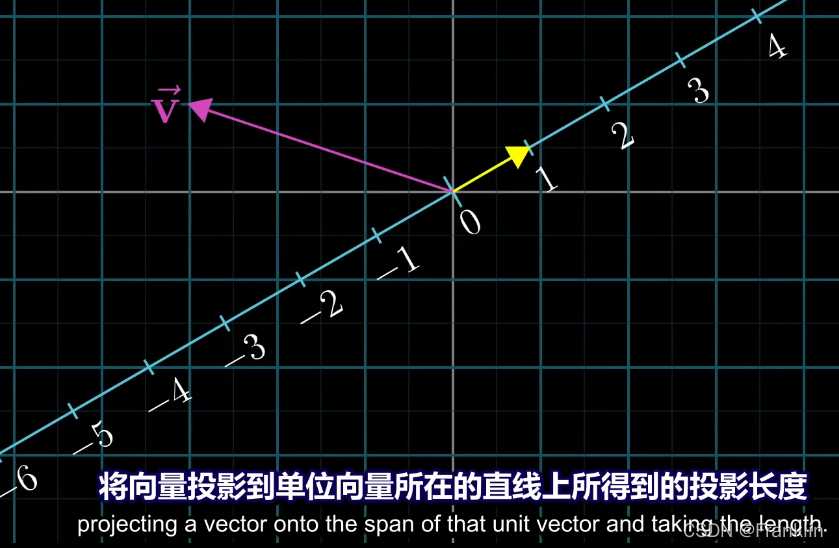
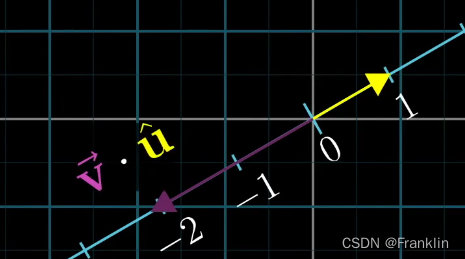
【注意上面，这里出现了向量v和单位向量u的点积】 V * ^u
上面，我们把一个单位向量【^u】的一个二维到一维的投射变换，推广到了任意向量V【x，y】投影到单位向量【^u】所张成空间的一个投射变换。现在，我们再推而广之，就是如果向量V,投射到非单位向量(所张成的空间）是什么情况呢？
1 假如我们将单位向量【^u】扩大3倍，
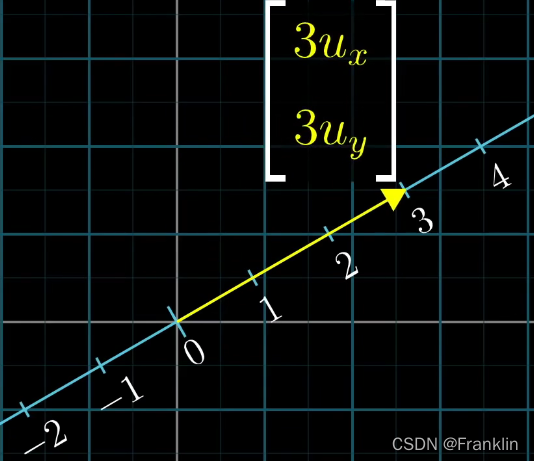
2 依据上小节的方法，可以得到投影变换矩阵如下
3 因为是线性的，可以看成是任意向量向斜着的数轴的投影，然后将结果乘以3
也就是与非给定单位向量的u的点积可以解读为：
首先，向给定的向量投影
然后，将投影的值乘以给定的非单位向量的长度。
【思考】由此，我们得到一个二维空间到数轴的线性变换，这个变换不是点积运算定义得到的，而是，通过将空间投影到给定的数轴来定义的。因为这个变换是线性的，所以，必须用1x2的矩阵表述，
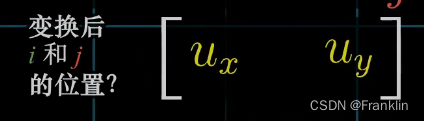
又因为这个1x2的矩阵与二维向量相乘的计算过程，和他的转置矩阵并求点积的计算过程相同，
这个投影变换，必然会与某个二维向量相关。
任何一个，二维到一维的线性变换，只要他 输出空间是一维的数轴，
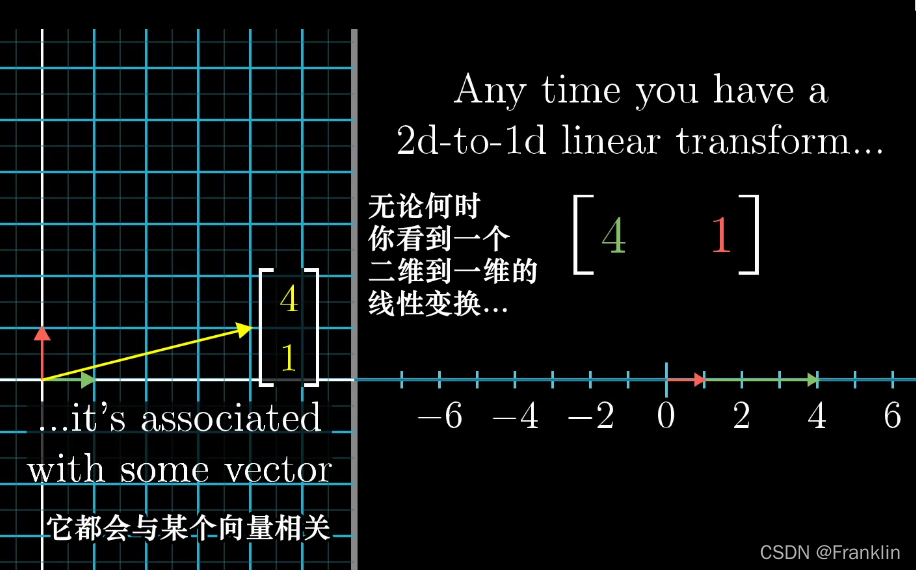
他都会和某个向量相关。这个线性变换【也就是这个1x2的矩阵相乘】和与这个相关的向量的点积做了同样的事情。
7 点积的应用：
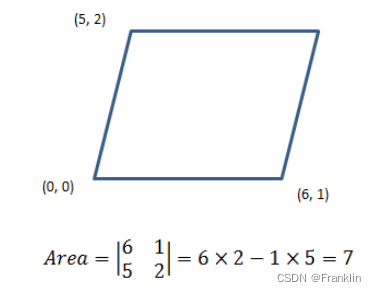
7.1 点积来计算面积：
7.1.1 例一
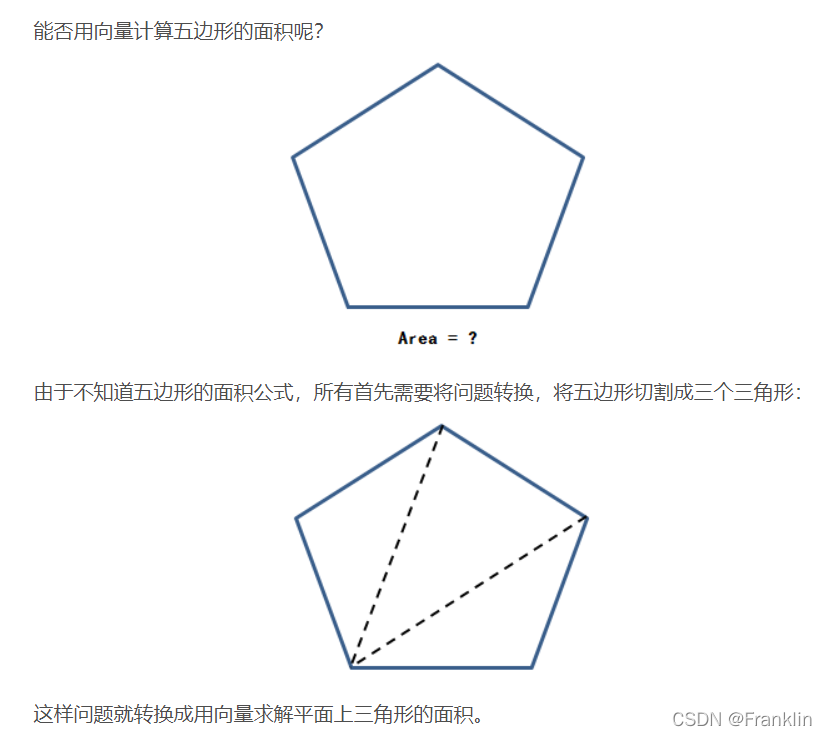
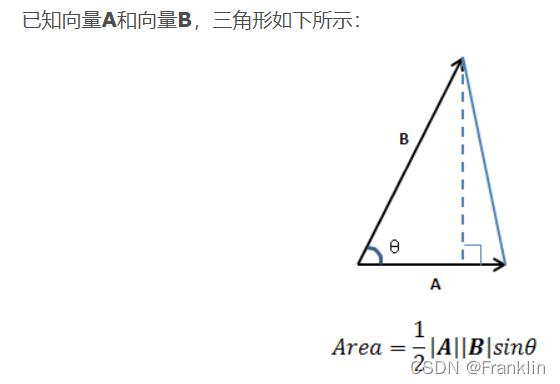
【案，这里和点积的公式已经很像了】
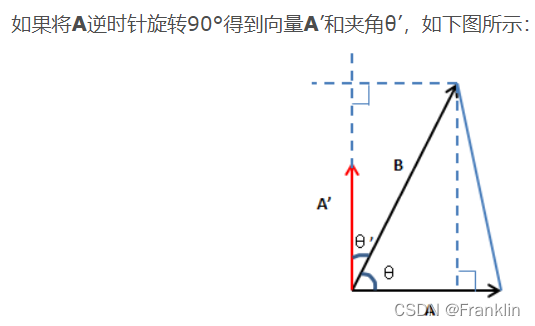
【这样就把点积可以用上了】
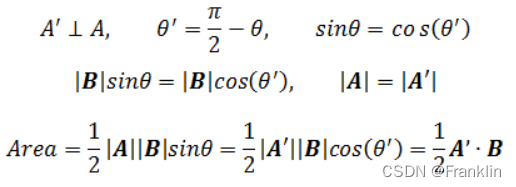
【现在求A'】
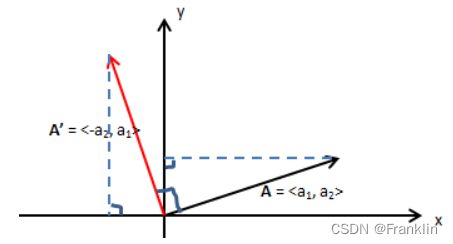
如果A = <a1, a2>，则A’ = A = <-a2, a1>，对于任意象限，该结论都适用。由此：
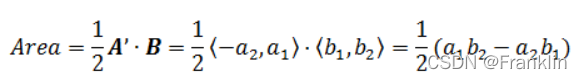
推而广之：计算平行四边形面积：‘
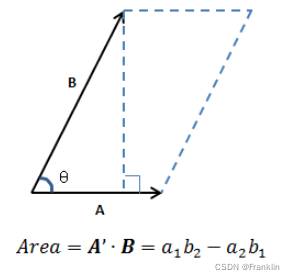
【案，这个公式和之前定义行列式的几何意义是一致的】
7.1.2 例二
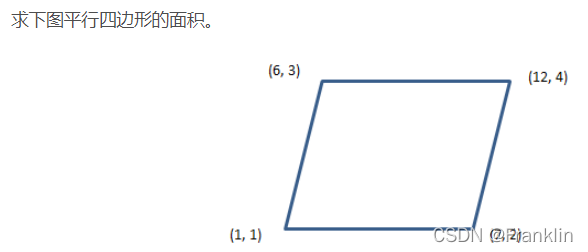
似乎是很简单的点积计算，需要注意的是，点积只对向量有意义，对普通的点则没有任何意义，所以需要把其中的两边转换成向量：
7.2 计算向量的角度
7.2.1 例一
-----------------------------------------
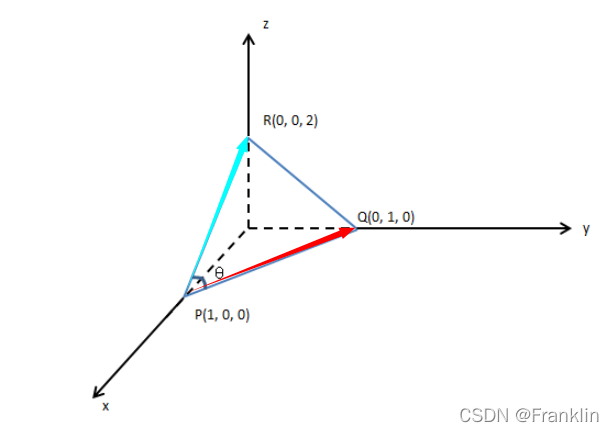
7.2.2 例二
例：i, j, k是不同的向量，求向量i +j + 2k， 2i –j + k间的夹角
7.2.3 例三
小结：
一个向量的对偶，是由他定义的线性变换。
一个线性变换的对偶，是某个特定的相关向量。
表面上看，点积知识理解投影的有利的一个几何工具：
例如：
鉴定向量的方向是否相同：
向量是否垂直：【正交性】
向量是否相反：
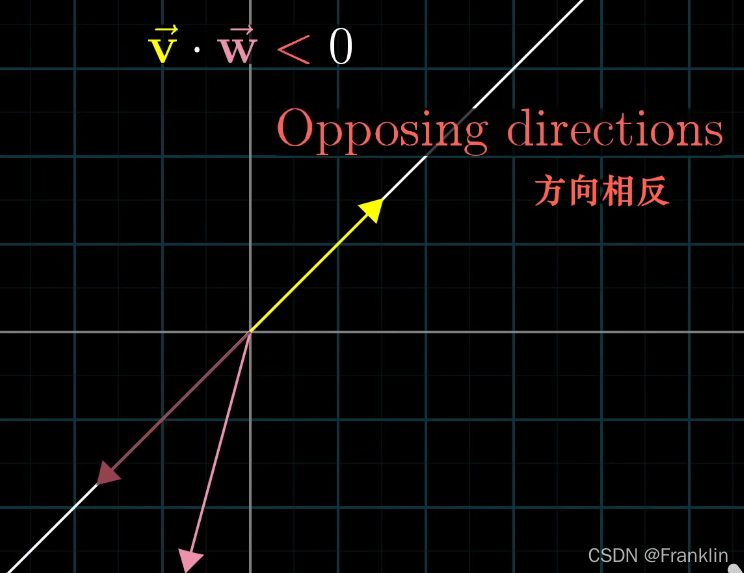
但是，从我们这节的研究来看，
两个向量的点积，就是
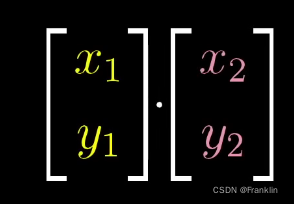
就是将其中一个向量变成了一个线性变换：虽然，点积和线性变换的数学计算过程一致，
向量不是空间的箭头，他是线性变换的物质载体。是一个特定变换的概念性记号。
(45条消息) 线性代数笔记3——向量2（点积）_我是8位的-CSDN博客
https://iam8bits.blog.csdn.net/article/details/78872549
(59条消息) 点乘 线性代数_线性代数笔记3——向量2（点积）_weixin_39890289的博客-CSDN博客https://blog.csdn.net/weixin_39890289/article/details/113018065
参考：
3Blue1Brown:“线性代数的本质”完整笔记 - 简书 (jianshu.com)
【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibili
词汇：
1 Dot product 点积
2 Duality 对偶性
3 Non-unit vector 非单位向量
4 Perpendicular 互相垂直
5 Symmetry对称性
