转置算子(transpose)的一种实现

transpose算子也叫做permute算子，根据白嫖有道英汉大词典的结果，他俩都是转置，改变排列顺序的意思。

算法逻辑是：

通过当前输出的一维偏移量(offset)计算输入矩阵对应的高维索引
然后根据参数pos重新排列输出索引，进而得到输出索引。
将输出索引转换成输入偏移量.
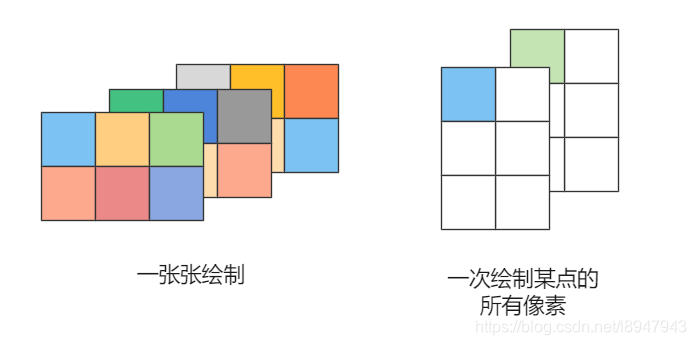
最后进行数据移动，整个过程的示意图如下.

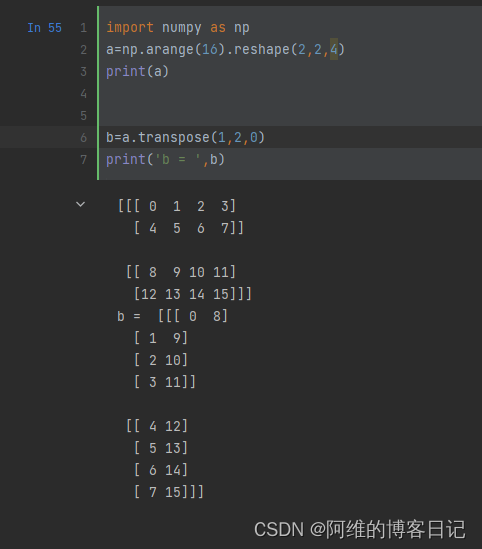
上代码，pos[]数组表示将输入矩阵的pos[i]维，映射到输出矩阵的第i维。

/** ===========================================================================================**       Filename:  transpose.c**    Description:  transpose operator impl.**        Version:   *         Create:  2021-11-07 14:08:50*       Revision:  none*       Compiler:  GCC:version 7.2.1 20170904 (release),ARM/embedded-7-branch revision 255204**         Author:  *   Organization:  Last Modified : 2021-11-07 20:22:56** ===========================================================================================*/
#include <stdio.h>
#include <stdlib.h>#define DBG(fmt, ...)   do{ printf("%s line %d, "fmt"\n", __func__, __LINE__, ##__VA_ARGS__); } while(0)void transpose_matrix(float *matrix_A, float **matrix_B, int *shape_A, int dims_A, int *pos)
{float *B;int element_count;int i;element_count = 1;for(i = 0; i < dims_A; i ++){element_count *= shape_A[i];}B = (float *)malloc(element_count * sizeof(float));if(B == NULL){DBG("malloc buffer for B failure.");return;}int* shape_B = (int *)malloc(sizeof(int) * dims_A);if(shape_B == NULL){DBG("malloc shape buffer for B failure.");return;}for(int i = 0; i < dims_A; i++){shape_B[i] = shape_A[pos[i]];}int* indexA = (int*)malloc(sizeof(int) * dims_A);if(indexA == NULL){DBG("failure to malloc matrix A index.");return;}int* indexB = (int*)malloc(sizeof(int) * dims_A);if(indexB == NULL){DBG("failure to malloc matrix B index.");return;}for(int src = 0; src < element_count; src++){int temp = src;for(i = dims_A-1; i >= 0; i--){indexA[i] = temp % shape_A[i];temp = temp / shape_A[i];}for(i = 0; i < dims_A; i++){indexB[i] = indexA[pos[i]];}int dst = 0;temp = 1;for(i = dims_A - 1; i >= 0; i--){dst = dst + indexB[i] * temp;temp = temp * shape_B[i];}B[dst] = matrix_A[src];}free(indexA);free(indexB);indexA = indexB = NULL;*matrix_B=B;return;
}void print_tensor(const float* A, int* shape, int dim)
{                     int elem = 1;     for(int i = 0; i < dim; i++){                 elem = elem * shape[i];}                 printf("Array size: %d\n", elem);for(int i = 0; i < elem; i++){                 printf( "%f ", A[i] );int split = 1;         for(int j = dim-1; j > 0; j--){                      split = split * shape[j];if( (i+1) % split == 0){printf("\n");}         }             }                 
} int main(void)
{float* B;float A[24] ={ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24};  int shapeA[] = {2, 3, 4}; int dimA = 3;print_tensor(A, shapeA, dimA);// Transposeint perm[] = { 2, 0, 1}; transpose_matrix(A, &B, shapeA, dimA, perm);// Print Bint shapeB[] = {4, 2, 3}; int dimB = 3;print_tensor(B, shapeB, dimB);int shapeM[] = {2, 2, 2, 3}; int dimM = 4;print_tensor(A, shapeM, dimM);// Transposeint permM[] = {3, 0, 1, 2}; transpose_matrix(A, &B, shapeM, dimM, permM);// Print Bint shapeO[] = {3, 2, 2, 2}; int dimO = 4;print_tensor(B, shapeO, dimO); // Free memoryfree(B);return 0;
}

运行结果

(base) caozilong@caozilong-Vostro-3268:~/Workspace/transpose$ ./a.out 
Array size: 24
1.000000 2.000000 3.000000 4.000000 
5.000000 6.000000 7.000000 8.000000 
9.000000 10.000000 11.000000 12.000000 13.000000 14.000000 15.000000 16.000000 
17.000000 18.000000 19.000000 20.000000 
21.000000 22.000000 23.000000 24.000000 Array size: 24
1.000000 5.000000 9.000000 
13.000000 17.000000 21.000000 2.000000 6.000000 10.000000 
14.000000 18.000000 22.000000 3.000000 7.000000 11.000000 
15.000000 19.000000 23.000000 4.000000 8.000000 12.000000 
16.000000 20.000000 24.000000 Array size: 24
1.000000 2.000000 3.000000 
4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 
10.000000 11.000000 12.000000 13.000000 14.000000 15.000000 
16.000000 17.000000 18.000000 19.000000 20.000000 21.000000 
22.000000 23.000000 24.000000 Array size: 24
1.000000 4.000000 
7.000000 10.000000 13.000000 16.000000 
19.000000 22.000000 2.000000 5.000000 
8.000000 11.000000 14.000000 17.000000 
20.000000 23.000000 3.000000 6.000000 
9.000000 12.000000 15.000000 18.000000 
21.000000 24.000000 (base) caozilong@caozilong-Vostro-3268:~/Workspace/transpose$

通过这个程序，发现一个很有意思的规律，大概描述如下，在N维空间下，<=N的tensor做转置，不需要对tensor做结构上的改变，只需要转换观察角度即可,因为空间维度容的下数据向各个方向的扩展.

以三维空间为例，对于二维矩阵的转置操作，我们只需要分别从列向量和行向量的方向上观察即可，不需要做矩阵做调整。

对于三维的物体也是一样，我们以魔方为例在说明：

不管魔方是几阶的，它都是三维的，都可以用一个三维的数组来表示。A[M][N][P],对于，M，N，P全排列中的任何一个，我们都可以通过切换观察视角来理解它的转置操作，而不需要对它做结构上的调整。

但是，当高维矩阵在内存中存储时，由于内存模型是线性表模型，它是一维的，一维的空间容不下多个维度，所以必须要扁平化 “降维” 成1维。对于N维tensor来说，这个降维排布方式有N！种方式。对应了高维空间中的几种观察视角的变化切换。

那么四维空间中魔方该如和表示置换操作呢？我们生活的空间是三维的，对于四维空间，我们缺乏像对三维空间那样直观的认识，更别说四维的魔方了。它超出了我们的认知范围，但是从数学的角度看，我们可以通过将第四维看成是是在某个三维方向上的拓展或者对某个维度的复用，还是以魔方为例，我们可以通过将组成魔方的每个小方块在划分维度，比如1维，2维。。。等等，想象一个魔方中的魔方，每个小方块还是一个魔方，那就是3*3*3*（3*3*3）六个维度，通过这种方式，我们可以定义任意维度的魔方，构造上有点像俄罗斯套娃。

但是，理解这种构造魔方的转置还有一个局限，就是它的维度已经超过了所在空间的维度，所有，有些维度会复用，造成“冲突”，还是以魔方为例，俄罗斯套娃方式构造的魔方，每个小方框其实都是对三维空间的复用，它不存在真正的它所在的高维对应的维度，所以，如果要完成置换，可能需要对魔方的构造进行调整，而不单单是仅仅是进行视角的变化。

这是由矩阵转置联想到的一点粗浅的理解，可能有错误，但这并不重要，每个人的认识都是在不断的纠正错误中前进的，权且记录下来，以便日后思考，更正吧。

总结：

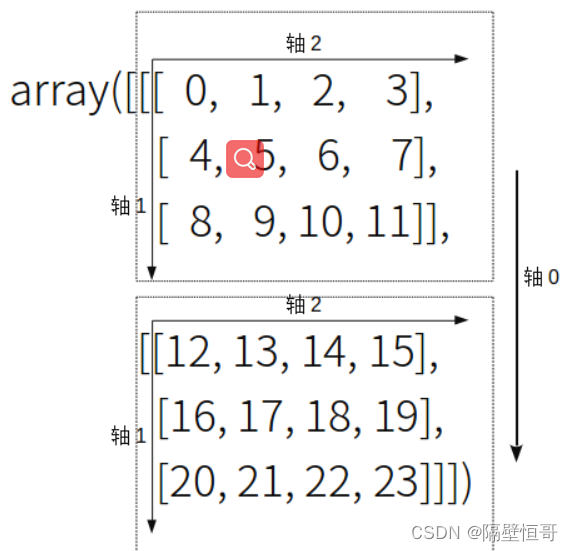
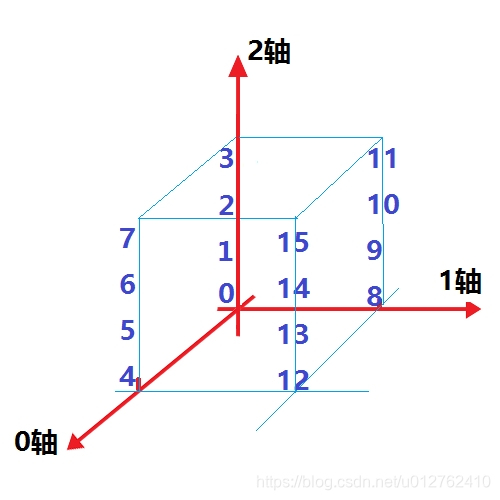
代码中，shape和数组形式定义的维度序关系如下:

imple by myself:

#include <stdio.h>int main(void)
{static int abc = 0;int a[6][6][3];int b[3][6][6];int i,j,k;for(i = 0; i < 6; i ++){for(j = 0; j < 6; j ++){for(k = 0; k < 3; k ++)a[i][j][k] =  abc ++;}}for(i = 0; i < 6; i ++){for(j = 0; j < 6; j ++){for(k = 0; k < 3; k ++)printf("%3d ", a[i][j][k]);printf("\n");}printf("\n");printf("\n");}printf("========================================\n");for(i = 0; i < 3; i ++){for(j = 0; j < 6; j ++){for(k = 0; k < 6; k ++)b[i][j][k] =  a[j][k][i];}}for(i = 0; i < 3; i ++){for(j = 0; j < 6; j ++){for(k = 0; k < 6; k ++)printf("%3d ", b[i][j][k]);printf("\n");}printf("\n");printf("\n");}return 0;
}