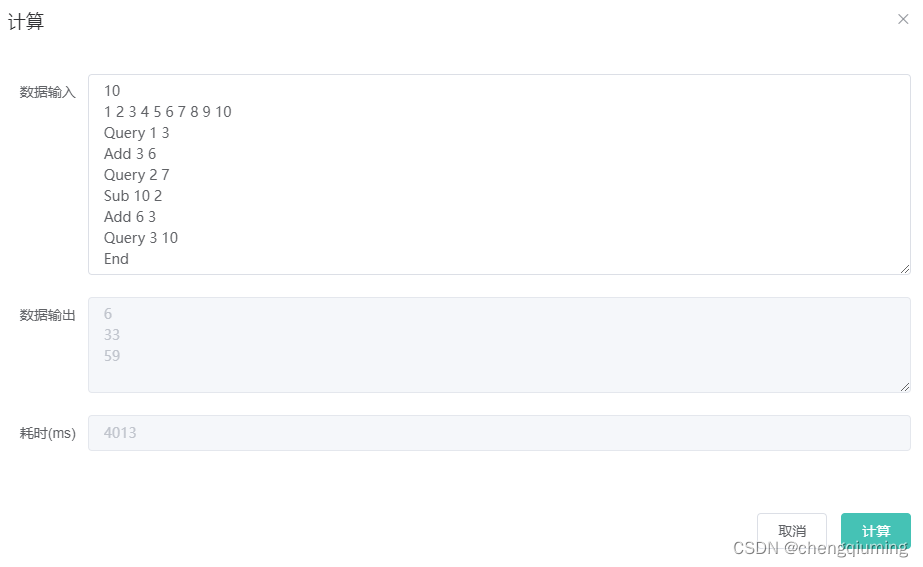
第四题:D-换队伍


分析:
1.问题本身很简单,也只有两条队伍,一个队伍中的人换到另一个队伍的末尾。问题在于对其他人排队位置的保存和排序。
2.用什么数据结构进行保存,是一个很关键的问题,对问题解决的方法和时间复杂度都有很大关系。如果使用简单的数组,那么每执行一次换队伍,会需要对后面的人进行前移一个位置,那么时间复杂度就上升了。
3.很显然,一看到题,第一个想法就是链表,使用两个链表分别表示两个队伍,每个人作为链表的一个结点。当执行换队伍操作时,从一个链表中删除一个结点然后加到另一个链表末尾。这个方法是可行的,但是由于只有两个队伍,因此还可以采取更直接的方法。比如直接用一个map,将第i个人映射到{队伍0或1,在队伍中序号}这样的映射对中。
4.题目中保证了给的序号是正常的(不会超限),因此不需要进行序号判断可以直接进行换队伍。且保证队伍一定会有一个人。
5.注意n1,n2最大为10^5,因此一共最多可以有2x10 ^5 个人。
6.还有一个问题,为什么不直接用两个数组来表示队伍,换队伍时在原位置置0,在另一个队伍末尾赋值人员编号。这样在每个人只换一次队伍时是简单办法,但是如果某人换两次队伍,就会存在找不到这个人的问题,这也是需要考虑的。
7.如果使用链表,要注意链表末尾结点要不同处理,判断下一结点是否指向NULL。
代码:
下面以别人提交的方案进行理解,来源均注明
方案1:https://ac.nowcoder.com/acm/contest/view-submission?submissionId=47614394
这个方案是代码量小。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int n1,n2,q;
int a[2][N*3],cnt[2];
int pos[N*2];
int main(){cin>>n1>>n2>>q;for(int i=1;i<=n1;i++){a[0][i]=i;pos[i]=i; //给队伍1的每个人赋值序号,pos存储位置}for(int i=1;i<=n2;i++){a[1][i]=i+n1;pos[i+n1]=N*10+i; //同理,给队伍2同样操作,但是把位置赋值 10N+i,避免与队伍1 的位置重复}cnt[0]=n1,cnt[1]=n2; //对两个队伍的人数 计数for(int i=1;i<=q;i++){ int x;cin>>x;if(pos[x]<N*10)a[1][++cnt[1]]=x,pos[x]=N*10+cnt[1];// 如果原本pos[x]小于10N,说明原来是队伍1的,那么把他放到队伍2的最末尾// 队伍2 ++cnt[1],计数加1,然后把这个人的位置赋值10N+cnt[1]else a[0][++cnt[0]]=x,pos[x]=cnt[0];// 反之,说明原来是队伍2的,那么队伍1 cnt[0]++// 然后把他放到队伍1末尾最后一个,位置赋值 cnt[0]}for(int i=1;i<=cnt[0];i++)if(pos[a[0][i]]==i)cout<<a[0][i]<<" ";cout<<endl;for(int i=1;i<=cnt[1];i++)if(pos[a[1][i]]==N*10+i)cout<<a[1][i]<<" ";cout<<endl;//最后进行一个判断输出
}
方案2:https://ac.nowcoder.com/acm/contest/view-submission?submissionId=47614831
基本和上面思路相同,存储队伍号,和在该队伍的位置,不同之处在于定义了一个结构体来存储
#include<bits/stdc++.h>
#define repo(i,c,n) for(int i = c; i < n; i++)
using namespace std;struct Pos{int que_num;int pos;
};int main()
{int n1,n2,q;cin>>n1>>n2>>q;//q1表示队伍1,q2表示队伍2vector<int> q1(n1+1),q2(n2+1);//定义一个辅助数组存储每个编号以及其在对应的队伍中的位置vector<Pos> que_num_pos(n1+n2+1);repo(i,1,n1+1){q1[i] = i;que_num_pos[i].que_num = 1;que_num_pos[i].pos = i;}repo(i,n1+1,n1+n2+1){q2[i-n1] = i;que_num_pos[i].que_num = 2;que_num_pos[i].pos = i-n1;}repo(i,0,q){int tmp;cin>>tmp;if(que_num_pos[tmp].que_num == 1){q1[que_num_pos[tmp].pos] = 0;que_num_pos[tmp].que_num = 2;n2++;que_num_pos[tmp].pos = n2;q2.emplace_back(tmp);}else{q2[que_num_pos[tmp].pos] = 0;que_num_pos[tmp].que_num = 1;n1++;que_num_pos[tmp].pos = n1;q1.emplace_back(tmp);}}//输出结果for(vector<int>::iterator iter = q1.begin(); iter != q1.end(); ++iter){if(*iter == 0) continue;cout<<*iter<<" ";}cout<<endl;for(vector<int>::iterator iter = q2.begin(); iter != q2.end(); ++iter){if(*iter == 0) continue;cout<<*iter<<" ";}return 0;
}
还有一种方案,大同小异,以一个数组来存队列号,两个数组分别存位置
方案3:
https://ac.nowcoder.com/acm/contest/view-submission?submissionId=47572108
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <set>using namespace std;
typedef long long LL;
typedef pair<int, int> PII;int a;
set<PII> s1, s2;
int mp[1000010];int main()
{int n1, n2, q;cin >> n1 >> n2 >> q;for (int i = 1; i <= n1; i ++){s1.insert({i, i});mp[i] = i;}for (int i = n1 + 1; i <= n1 + n2; i ++){s2.insert({i, i});mp[i] = i;}int idx = n1 + n2;while (q --){cin >> a; // a 为人员编号 mp[a]为位置if (s1.count({mp[a], a})) //count()--返回某个值元素的个数,这里存在就执行if{s1.erase({mp[a], a}); //erase()--删除集合中的元素mp[a] = ++ idx;s2.insert({mp[a], a});//insert()--在集合中插入元素}else{s2.erase({mp[a], a});mp[a] = ++ idx;s1.insert({mp[a], a});} // 改变位置都是排在最后,那么只要把 mp[a]赋值为当前最大值} // 然后加到对应的红黑树 s1或s2 中,会自动按键值大小排序,最后输出for (auto x:s1)cout << x.second << ' ';cout << endl;for (auto x:s2)cout << x.second << ' ';
}
https://www.cnblogs.com/yoke/p/6867302.html
set和pair 结合使用
2.元素的插入与中序遍历
采用inset()方法把元素插入到集合中,插入规则在默认的比较规则下,
是按元素值从小到大插入,如果自己指定了比较规则函数,则按自定义比较规则函数插入。
使用前向迭代器对集合中序遍历,结果正好是元素排序后的结果。
s.insert(5); //第二次插入5,重复元素,不会插入
4.元素的删除
与插入元素的处理一样,集合具有高效的删除处理功能,并自动重新调整内部的红黑树的平衡。
set中每个元素的值都唯一,而且系统能根据元素的值自动进行排序