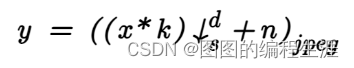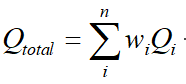2020年中兴捧月傅里叶派决赛题目

article/2025/10/14 3:56:31

 

目录

题目：

模型建立

题目分析

注意的小问题

计算结果

 代码

模型改进和精细预测

写在最后

题目：

假设：

  1. 病毒正在一个居民总数为N=100,000, \small R_a=25\% 的城市里扩散。在我们研究的时间段内（300天），没有新生儿出生，也没有死亡病例发生
  2. 所有居民按照其自身年龄，可以划分为：未成年，青壮年和中老年。根据事先统计，未成年占比为Rc=25%，青壮年占比为Ra=55%，中老年占比为Ro=20%。
  3. 所有居民按照其感染情况，可以划分为：健康者，潜伏者，发病者和康复者
  4. 病毒传播过程如下：

  •      每天健康者接触到潜伏者后，根据其所在的年龄类别（未成年，青壮年和中老年）分别以概率\beta_c^e, \beta_a^e和\beta_o^e变为潜伏者

  • 每天健康者接触到发病者后，根据其所在的年龄类别（未成年，青壮年和中老年）分别以概率\beta_c^i, \beta_a^i和\beta_o^i为潜伏者
  • 每天所有年龄类型的潜伏者都以概率α变为发病者（α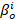的取值范围在0.01~0.05）
  • 每天发病者根据其所在的年龄类别（未成年，青壮年和中老年），分别以概率γc, γa和γo变为康复者
  • 康复者在所研究的时间段内（300天）不再被感染和感染别人
  • 在研究的时间段内（300天），每人每天接触的人数r=10，且所有人两两接触的概率相等

以上就是题目的假设，同时给出前面四十天的数据：如下图所示，一共有四十天的数据

发病者　康复者
未成年青壮年中老年 未成年青壮年中老年
112125305 568773
92115302 839887
79110309 102114106
68107316 119129122
65107332 136138134
64110353 149152152

模型建立

通过题目的分析，可以知道，这个题目要首先建立一个模型，然后根据数据进行估算回原本的参数，通过简单的查询资料，我们可以知道，关于病毒模型，网上很多，包括SI,SEI,SEIR模型等，通过对模型的分析，可以知道，这个题目比较适合SEIR模型，

于是建立SEIR模型：

 

 

 

 说明：S，E，I，R 分别表示的是，S:易感人群，也就是健康人群，  E:暴露人群，也就是潜伏者，I：患病人群，R：健康人群。

第一个公式的意思：S_n人群当前阶段的数量是上一个阶段的数量 \large S_{n-1}减去上一个阶段\large S_{n-1}人群中转换为E_n暴露人群的数量，

第二个公式的意思：E_n人群的当前数量是上一个E_{n-1}的数量加上\large S_{n-1}阶段转换的人群，减去E_{n-1}转换为I_n的数量

第三个公式的意思:I_n的数量是上一个阶段I_{n-1}的数量加上E_{n-1}转换为I_n的数量，然后减去I_{n-1}中康复的数量

第四个公式意思：R_n是数量等于R_{n-1}阶段的数量加上I_{n-1}中康复的数量

注意的小问题：上面列出来的公式，只是children 未成年人的公式，其实每个年龄段都有四个一样的公式，但是都是一样的，只是下标不同，但是值得注意的是三个年龄段中的I^{total}_n,E^{total}_n表示的是目前三个年龄阶段中所有的暴露人群和患病人群的总数，并不是三个年龄段各自的暴露人群和患病人群。

         说明一下：这里的易感人群转换为暴露人群的公式，是一个近似是公式。他计算的是每个暴露人群碰到的易感人群的数量后转换成暴露人去的个数  +  每个患病人群加上易感人群并转换为暴露人群的数量。这个假设成立的条件是：每个暴露人群碰到一个易感易感人群，易感人群的感染率就增加，每个患病人群碰到易感易感人群，易感人群的感染概率也是增加的。换句话说，对于每个易感人群，他转换的概率是和碰到暴露人群和患病人群的数量有关系的，数量越多，感染的概率就越大。 同时，暴露人群碰到每个人的概率是相同的。患病人群碰到每个人的概率也是相同的。 这个概率不会因为前面碰到的人是什么类型的而改变。当数量很大的时候，应该是近似相等的。如果想更加具体的模型，应该是可以用C（n,m），也就是排列组合来严格计算。但是实际计算发现，N=100000的时候计算机已经计算不过来了。最后还是用了这个模型来计算。

       我也曾经尝试过用其他的转换概率模型。比如说假设每个易感人群只要碰到暴露人群并且不接触患病人群，不管是碰到几个暴露人群，那么感染概率都是相同的，也就是\beta_c^e, \beta_a^e和\beta_o^e。  每个易感人群只要是碰到患病人群，不管碰到几个患病人群，那么他的感染概率都是\beta_c^i，\beta_a^i或者是\beta_o^i。  也就是说。我认为碰到患病人群后的感染概率要高于碰到暴露人群，并且覆盖了碰到了暴露人群的感染概率。和碰到的数量没有关系。因为，我认为，只要碰到了暴露人群或者是患病人群，易感人群就类似于碰到了病菌了，不管是碰到多少个病菌，转换为携带者的概率都是相同的。而且患病人群的病菌要比携带者更毒一点，所以覆盖了暴露人群的病菌  但是，经过实际的检验。发现基于这个建立的模型，拟合的结果不是那么完美。所以我猜测。对于易感人群，转换为暴露人群的概率和碰到暴露人群和患病者的数量是有关系的。

     以上是个人的理解，不知道自己的理解有没有问题。但是查询到网上的模型都是这个。整个模型唯一的近似的地方也就是易感人群转换为暴露人群的地方了。后面的 更加精细的模型也就是算更加准确的转移概率了！当然了，整个模型除了这个地方，其他地方都是很直白的。也没有什么好精细的建模的~~

题目分析

首先，我们可以看看我们目前已经知道什么条件，我们可以知道前面四十天的暴露人群和易感人群的每天的数量，患病人群的每天的数量，康复者的每天的数量。然后，我们分析一下，我们要求的参数，发现可以大致的分成三类

  1. γc, γa和γo  
  2. α
  3. \beta_c^e, \beta_a^e，\beta_o^e 和\beta_c^i, \beta_a^i和\beta_o^i

 

首先，第一类的参数和其他的参数简直是没有关系。可以直接通过公式计算出来。

也是就是：\gamma =\frac{R_n-R_{n-1}}{I_{n-1}}  这也就可以简单的计算出来了：计算后画个图，如下：

      所以可以非常容易的求出了，不管是求平均还是后面的加权求平均，都可以非常容易的计算出来。

第二个参数的求取和第三类的参数求取是关联的，如果知道第二个参数，那么其实根据现在的α 是可以计算出来每个\beta_c^e, \beta_a^e，\beta_o^e 和\beta_c^i, \beta_a^i和\beta_o^i的。

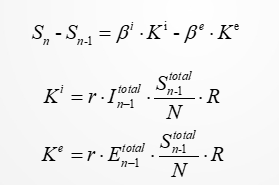
第二个参数的，和其他的参数的关系可以变成如图所示，假设我们知道了 α 那么，对于每个阶段，其实都有一个上面的方程，同时每个阶段的K^i和K^e是知道的，那么我们可以获取若干个这种类似于二元一次方程的等式，那么我们就可以用最小二乘法类型的方式来计算出\beta_c^e, \beta_a^e，\beta_o^e 和\beta_c^i, \beta_a^i和\beta_o^i。

所以我们可以假设一个α ，通过两个时间阶段的值，求出\beta_c^e, \beta_a^e，\beta_o^e 和\beta_c^i, \beta_a^i和\beta_o^i。然后预测第三个阶段的S+W的值，根据预测的结果来判断α的值预测的是不是正确的。

注意的小问题

（1）首先，我们可以基本上肯定，如果碰上患病人群的感染概率一定是大于碰上潜伏者的感染概率。所以我们在计算的时候，可以加上限制条件 \beta^e<\beta^i 。具体到Matlab公式是怎么样的嘞

我们可以改变第二项的计算是前两项的和，并且限制两个待求的参数都是大于0的，然后重新计算一下第二项系数。

（2） 通过实际的计算可以发现如果直接计算老年人群体里面的易感人群，你会发现，易感人群是波动的，同时在后期，比如33天后，数量居然会回升，如下图所示，下图中蓝色线条和橙色线条是易感人群，红色和蓝色是易感人群的一阶微分的负数。这个回升显然是非常不合理的。这样计算出来的\beta一定是会有负数的。这个地方，我不知道的处理方式是用多阶的线性方程模拟一下，近似于进行了滤波操作，同时，计算\beta的区间只选择中间的阶段，因为中间的阶段看上要正常很多。应该有其他的处理方式，比如说，剔除掉一阶微分中为符号反常的数据。 我这里只是简单的多阶拟合一下，然后取中间的比较好的数据段。

其他的年龄段的计算还是比较正常的，但是应该也可以shaxuan 

计算结果

最终的计算结果和仿真如下图所示，其中α=0.434 。大概率是比较接近的

 然后预测后面的人数如下图所示：

 代码

  代码如下：

clc;
clear all;r = 10;exc = xlsread('Data.xlsx');
Ic = exc(:,1);
Ia = exc(:,2);
Io = exc(:,3);Rc = exc(:,5);
Ra = exc(:,6);
Ro = exc(:,7);TRc=diff(Rc)./Ic(1:39);
gamma_c = mean(TRc(10:39));TRa=diff(Ra)./Ia(1:39);
gamma_a = mean(diff(Ra)./Ia(1:39));TRo=diff(Ro)./Io(1:39);
gamma_o = mean(TRo(10:39));% figure(1);
% plot([1:39],TRc, [1:39],TRa, [1:39],TRo); 
% title('三个阶段的gamma');%遍历 a 求最小均方根误差的值
N=100000;
NumberOfDivition=1000;
RMS = zeros(NumberOfDivition,3);
a=0.01:(0.05-0.01)/NumberOfDivition:0.05;
beta_c_list=zeros(NumberOfDivition,2);
beta_a_list=zeros(NumberOfDivition,2);
beta_o_list=zeros(NumberOfDivition,2);
for k =1:NumberOfDivitionSEc=20000 - Ic - Rc;SEa=20000 - Ia - Ra;SEo=20000 - Io - Ro;Ec=-diff(SEc)/a(k);Ea=-diff(SEa)/a(k);Eo=-diff(SEo)/a(k);Sc = 25000 - Ic(1:39) - Rc(1:39) - Ec;Sa = 55000 - Ia(1:39) - Ra(1:39) - Ea;So = 20000 - Io(1:39) - Ro(1:39) - Eo;So_old=So;p = polyfit([1:39]' ,So, 4);  %p为拟合后的多项式系数So=polyval(p, [1:39]' );S_all =Sc +Sa +So;E_all = Ec + Ea + Eo;I_all = Ic + Ia + Io;R_all =Rc+Ra+Ro;%     figure
%     plot([1:39]' , So, [1:39]', Eo(1:39),   'linewidth',2);ttc = 10*Sc.*I_all(1:39)./N; ssc = 10*(Sc).*E_all(1:39)./N; xc=[ssc(1:38),ttc(1:38)];tta =  10*Sa.*I_all(1:39)./N;   ssa = 10*(Sa).*E_all(1:39)./N; xa=[ssa(1:38),tta(1:38)];tto =  10*So.*I_all(1:39)./N;   sso = 10*(So).*E_all(1:39)./N; xo=[sso(1:38),tto(1:38)];Yc = -diff(Sc);Ya = -diff(Sa);Yo = -diff(So);Yo_old=-diff(So_old);
%     plot([1:39],So, [1:38], Yo,[1:39],So_old, [1:38], Yo_old,'linewidth',2);
%     title('群体：老年人中的易感人群');fun=inline('c(1).*x(:,1)+(c(1)+c(2)).*x(:,2)','c','x');beta_c = lsqcurvefit(fun,[0.01 0.01],xc(10:35,:),Yc(10:35),[0,0],[0.5,0.5]);beta_a = lsqcurvefit(fun,[0.01 0.01],xa(10:35,:),Ya(10:35),[0,0],[0.5,0.5]);beta_o = lsqcurvefit(fun,[0.01 0.01],xo(5:30,:),Yo(5:30),[0,0],[0.5,0.5]);beta_c(2)=beta_c(1)+beta_c(2);beta_a(2)=beta_a(1)+beta_a(2);beta_o(2)=beta_o(1)+beta_o(2);beta_c_list(k,1)=beta_c(1);  beta_c_list(k,2)=beta_c(2);beta_a_list(k,1)=beta_a(1);  beta_a_list(k,2)=beta_a(2);beta_o_list(k,1)=beta_o(1);  beta_o_list(k,2)=beta_o(2);%testY = beta_c(1).*E_all(1:38) + beta_c(2).*I_all(1:38);%plot([1:38],Yc,[1:38], testY)%初值Ic_diff = diff(Ic);Ia_diff = diff(Ia);Io_diff = diff(Io);Ic_ans = Ic(1);Ia_ans = Ia(1);Io_ans = Io(1);Rc_ans = Rc(1);Ra_ans = Ra(1);Ro_ans = Ro(1);Ec_ans = (Ic_diff(1) + gamma_c.*Ic(1))./a(k);Ea_ans = (Ia_diff(1) + gamma_a.*Ia(1))./a(k);Eo_ans = (Io_diff(1) + gamma_o.*Io(1))./a(k);Sc_ans = 25000 - Ic_ans - Rc_ans - Ec_ans;Sa_ans = 55000 - Ia_ans - Ra_ans - Ea_ans;So_ans = 20000 - Io_ans - Ro_ans - Eo_ans;for i = 2:40Ic_ans(i) = Ic_ans(i-1) + a(k) * Ec_ans(i-1) - gamma_c * Ic_ans(i-1);Ia_ans(i) = Ia_ans(i-1) + a(k) * Ea_ans(i-1) - gamma_a * Ia_ans(i-1);Io_ans(i) = Io_ans(i-1)+ a(k) * Eo_ans(i-1)-gamma_o * Io_ans(i-1);Rc_ans(i) = Rc_ans(i-1) + gamma_c*Ic_ans(i-1);Ra_ans(i) = Ra_ans(i-1) + gamma_a*Ia_ans(i-1);Ro_ans(i) = Ro_ans(i-1) + gamma_o*Io_ans(i-1);Ec_ans(i) = Ec_ans(i-1) + r * Sc_ans(i-1)/100000*( beta_c(1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_c(2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Ec_ans(i-1);Ea_ans(i) = Ea_ans(i-1) + r * Sa_ans(i-1)/100000*( beta_a(1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_a(2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Ea_ans(i-1);Eo_ans(i) = Eo_ans(i-1) + r * So_ans(i-1)/100000*( beta_o(1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_o(2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Eo_ans(i-1);Sc_ans(i) = 25000 - Ic_ans(i) - Rc_ans(i) - Ec_ans(i);Sa_ans(i) = 55000 - Ia_ans(i) - Ra_ans(i) - Ea_ans(i);So_ans(i) = 20000 - Io_ans(i) - Ro_ans(i) - Eo_ans(i);end%     figure
%     plot([1:40],Ic,[1:40],Ic_ans(1:40));
%     title('人群：青年')
%     figure
%     plot([1:40],Ia,[1:40],Ia_ans(1:40));
%     title('人群：成年人')
%     figure
%     plot([1:40],Io,[1:40],Io_ans(1:40));
%     title('人群：老年人')%均方根误差RMS(k,1) = sum(sqrt((Ic_ans-Ic').^2))/40;RMS(k,2) = sum(sqrt((Ia_ans-Ia').^2))/40;RMS(k,3) = sum(sqrt((Io_ans-Io').^2))/40;
end% 找到最小误差点
RMS_mean = (RMS(:,1)+RMS(:,2)+RMS(:,3))/3;
%RMS_mean = RMS(:,1);
k = find(RMS_mean == min(RMS_mean));
for i = 2:300Ic_ans(i) = Ic_ans(i-1) + a(k) * Ec_ans(i-1) - gamma_c * Ic_ans(i-1);Ia_ans(i) = Ia_ans(i-1) + a(k) * Ea_ans(i-1) - gamma_a * Ia_ans(i-1);Io_ans(i) = Io_ans(i-1)+ a(k) * Eo_ans(i-1)-gamma_o * Io_ans(i-1);Rc_ans(i) = Rc_ans(i-1) + gamma_c*Ic_ans(i-1);Ra_ans(i) = Ra_ans(i-1) + gamma_a*Ia_ans(i-1);Ro_ans(i) = Ro_ans(i-1) + gamma_o*Io_ans(i-1);Ec_ans(i) = Ec_ans(i-1) + r * Sc_ans(i-1)/100000*( beta_c_list(k,1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_c_list(k,2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Ec_ans(i-1);Ea_ans(i) = Ea_ans(i-1) + r * Sa_ans(i-1)/100000*( beta_a_list(k,1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_a_list(k,2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Ea_ans(i-1);Eo_ans(i) = Eo_ans(i-1) + r * So_ans(i-1)/100000*( beta_o_list(k,1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_o_list(k,2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Eo_ans(i-1);Sc_ans(i) = 25000 - Ic_ans(i) - Rc_ans(i) - Ec_ans(i);Sa_ans(i) = 55000 - Ia_ans(i) - Ra_ans(i) - Ea_ans(i);So_ans(i) = 20000 - Io_ans(i) - Ro_ans(i) - Eo_ans(i);
endsubplot(2,3,1);
plot([1:40],Ic,[1:40],Ic_ans(1:40));
title('人群：青年')
subplot(2,3,2);
plot([1:40],Ia,[1:40],Ia_ans(1:40));
title('人群：成年人')
subplot(2,3,3);
plot([1:40],Io,[1:40],Io_ans(1:40));
title('人群：老年人')subplot(2,3,4);
plot([1:300],Ic_ans,[1:300],Rc_ans,[1:300],Ec_ans,[1:300],Sc_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：青年')subplot(2,3,5);
plot([1:300],Ia_ans,[1:300],Ra_ans,[1:300],Ea_ans,[1:300],Sa_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：成年人')subplot(2,3,6);
plot([1:300],Io_ans,[1:300],Ro_ans,[1:300],Eo_ans,[1:300],So_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：老年')r=1;
for i = 40:300Ic_ans(i) = Ic_ans(i-1) + a(k) * Ec_ans(i-1) - gamma_c * Ic_ans(i-1);Ia_ans(i) = Ia_ans(i-1) + a(k) * Ea_ans(i-1) - gamma_a * Ia_ans(i-1);Io_ans(i) = Io_ans(i-1)+ a(k) * Eo_ans(i-1)-gamma_o * Io_ans(i-1);Rc_ans(i) = Rc_ans(i-1) + gamma_c*Ic_ans(i-1);Ra_ans(i) = Ra_ans(i-1) + gamma_a*Ia_ans(i-1);Ro_ans(i) = Ro_ans(i-1) + gamma_o*Io_ans(i-1);Ec_ans(i) = Ec_ans(i-1) + r * Sc_ans(i-1)/100000*( beta_c_list(k,1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_c_list(k,2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Ec_ans(i-1);Ea_ans(i) = Ea_ans(i-1) + r * Sa_ans(i-1)/100000*( beta_a_list(k,1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_a_list(k,2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Ea_ans(i-1);Eo_ans(i) = Eo_ans(i-1) + r * So_ans(i-1)/100000*( beta_o_list(k,1)*(Ec_ans(i-1) + Ea_ans(i-1) + Eo_ans(i-1)) + beta_o_list(k,2)*(Ic_ans(i-1)+Ia_ans(i-1)+Io_ans(i-1)) ) - a(k)*Eo_ans(i-1);Sc_ans(i) = 25000 - Ic_ans(i) - Rc_ans(i) - Ec_ans(i);Sa_ans(i) = 55000 - Ia_ans(i) - Ra_ans(i) - Ea_ans(i);So_ans(i) = 20000 - Io_ans(i) - Ro_ans(i) - Eo_ans(i);
end
subplot(1,3,1);
plot([1:300],Ic_ans,[1:300],Rc_ans,[1:300],Ec_ans,[1:300],Sc_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：青年')subplot(1,3,2);
plot([1:300],Ia_ans,[1:300],Ra_ans,[1:300],Ea_ans,[1:300],Sa_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：成年人')subplot(1,3,3);
plot([1:300],Io_ans,[1:300],Ro_ans,[1:300],Eo_ans,[1:300],So_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：老年')I_ans=Ic_ans+Ia_ans+Io_ans;
R_ans=Rc_ans +Ra_ans+Ro_ans;
S_ans=Sc_ans+Sa_ans+So_ans;figure;
plot([1:300],I_ans,[1:300],Ro_ans,[1:300],R_ans,[1:300],S_ans,'linewidth',2);
legend('Infectious people','Recovered people','Exposed people','Susceptible people');
xlabel('天数')
ylabel('人员数量')
title('人群：总的人群')

模型改进和精细预测

   整个模型中，易感人群转换为暴露人群的概率和数量应该是可以进一步精细的。比如说用蒙特卡罗方法来模拟N个人群中随机碰撞的情况，然后计算下一个阶段的人群的不同数量情况，例如，可以将某个阶段中N个人群的随机分布，期中的不同年龄阶段的暴露人群和患病人群，易感人群和移出人群都随笔分布，然后计算每个易感人群前后的10个人中的易感人群和患病人群的情况，计算这个人的转换概率，然后遍历一下，计算出新的人群数量的分布。

写在最后

        本次的比赛，让我感触良多，对最后的结果也很可惜。但是仔细想想，也没有什么可惜的，自己确实是没有比别人做的更好。自己身上还是有很大的不足，其实一直有意识到自己的不足。但是并没有什么行动，但是这一次，感觉更加深刻， 如果当时可以头脑更加清晰一点，运算过程更加清晰一点，代码更加清晰一点，写的过程更加仔细一点。也许结果会更好一点。

      到了这个年龄段，有时候会意识到，自己未来短暂时间的所有可以取得的成绩，都是之前所有努力，所有选择的影响。人应该一直保持进步，一直积极向上。积极改变自己身上的陋习，这个过程可能会比较难，也比较漫长，效果也是非短期可见的。但是，还是要试一试。

    慢慢尝试改变自己，人生也还很长，未来可期。做人还是要开心~！

附件：

        每天的数据：

发病者　康复者
未成年青壮年中老年 未成年青壮年中老年
112125305 568773
92115302 839887
79110309 102114106
68107316 119129122
65107332 136138134
64110353 149152152
66119381 166167169
69129414 178181189
74145454 192196208
82162505 209212234
94182563 230232256
107209633 252251285
125242713 276277317
145276806 305304353
165319908 334338393
1933701031 373379437
2174271165 415421489
2504941315 468472546
2865671478 524529615
3266541665 590601686
3747481864 663678769
4208532080 748767862
4779742314 846869969
53511042561 9549851084
60212492818 107811161212
67114033084 121212661351
74515743360 136814341504
81917623639 154116231672
90319583917 172518351855
98121654189 193320702049
106923844455 215723292261
115526114708 240426132481
123628484948 266929282719
132030915173 295032672967
140433385376 325436403225
147835885562 357740413490
155538375727 391844683770
162340845876 427549324054
168543296002 464454214351
174345676105 503359374651

http://chatgpt.dhexx.cn/article/V8dScb8m.shtml

相关文章

2022中兴捧月算法挑战赛（RAW图像去噪）——初赛到决赛总结与反思

2022中兴捧月算法挑战赛（RAW图像去噪）——初赛到决赛总结与反思

文章目录 1. 初赛经历&炼丹详情1.1 初赛经历1.2 炼丹详情 2、复赛经历&反思与总结2.1 复赛经历2.2 复赛反思 3、决赛经历&反思与总结3.1 决赛题目3.2 决赛思路总结3.3 冠军方案记录3.4 决赛经历3.5 决赛反思 1. 初赛经历&炼丹详情 1.1 初赛经历 最后分数57.2…
阅读更多...
2020中兴捧月算法大赛迪杰斯特拉赛道初赛题解

2020中兴捧月算法大赛迪杰斯特拉赛道初赛题解

目录 摘要1 程序中使用的数据结构1.1 几个基本数据类型1.2 车道(Lane)1.3 道路(Road)1.4 站点(Station)1.5 货物(Goods)1.6 系统资源(SystemResource)1.7 物流系统(LogisticsSystem) 2 算法思路2.1 初赛初版&#xff1a;路由表、深度优先搜索、路径惩罚2.1.1 搜索策略2.1.2 路径…
阅读更多...
中兴捧月营销精英挑战赛回顾

中兴捧月营销精英挑战赛回顾

先上图 为期四天的比赛结束了&#xff0c;把这次比赛的收获做一个总结和分享。希望能帮上后面有需要的同学吧。 主要内容分为比赛流程、决赛内容和心得体会三部分。 一.比赛流程 比赛流程分为三部分&#xff0c;初赛、复赛和决赛。初赛开始需要每位同学从瑞伊、加勒斯和奥格…
阅读更多...
2023中兴捧月图像赛道-任意尺度盲超分初赛第三方案

2023中兴捧月图像赛道-任意尺度盲超分初赛第三方案

任意尺度盲超分-初赛第三方案 吐槽篇方案篇一、左脚踩右脚二、梯度攻击 建议篇 吐槽篇 正文内容.正式讲述方案之前&#xff0c;容我先吐槽两句&#xff0c;真tm的是比赛&#xff0c;纯纯ex人。学历厂就别打着以赛招聘的口号&#xff0c;要985计算机的直接去他们学校里宣讲嘛&am…
阅读更多...
中兴捧月之旅

中兴捧月之旅

上个月底&#xff0c;我怀着激动的心情来到古都西安参加了第十一届中兴捧月算法大赛的全国总决赛&#xff0c;因为这是我第一次参加的线下封闭开发的现场竞赛&#xff0c;特以此文记录这趟快乐的西安之旅。 中兴捧月是中兴通讯公司举办的大型算法比赛&#xff0c;今年共有6大赛…
阅读更多...
2020中兴捧月算法大赛——傅里叶赛道 第1名方案

2020中兴捧月算法大赛——傅里叶赛道 第1名方案

大家好&#xff0c;我是轶扬。 最近我在总结研究生阶段参与的一些项目和比赛&#xff0c;翻到了2020年参加的中兴捧月算法大赛&#xff0c;题目很有意思&#xff0c;解法上也有一些有趣的创新&#xff0c;所以拿出来特别记录一下。 中兴捧月算法大赛是中兴通讯公司主办的算法赛…
阅读更多...
2023 中兴捧月算法挑战赛-自智网络-参赛总结

2023 中兴捧月算法挑战赛-自智网络-参赛总结

“中兴捧月”是由中兴通讯面向在校大学生举办的全球性系列赛事活动&#xff0c;致力于培养学生建模编程、创新、方案策划和团队合作能力。今年是在学校的宣传下了解到比赛&#xff0c;最初抱着学习的态度报名了比赛&#xff0c;最终进入了决赛&#xff0c;完成了封闭的开发与赛…
阅读更多...
谈谈中兴捧月大赛决赛以及总结

谈谈中兴捧月大赛决赛以及总结

前言 四月份&#xff0c;在师兄的推荐下&#xff0c;报名参加了中兴捧月大赛。一开始只是为了混一个面笔试的资格&#xff08;因为提交有效成绩即可免笔试&#xff09;&#xff0c;然后为了找一个简单的赛道&#xff0c;注册了几个号看了两三个赛道的题目。发现自己每个都不熟…
阅读更多...
我得重新集结部队（模拟）

我得重新集结部队（模拟）

思路&#xff1a;感觉问题不大&#xff0c;不知道为啥一直WA WA代码&#xff1a; package 练习; import java.util.*; import java.io.*; import java.lang.*; public class Main{public static void main(String[] args) {Scanner scnew Scanner (System.in);int nsc.nextInt…
阅读更多...
攻防演习紫队第一篇之介绍和组织

攻防演习紫队第一篇之介绍和组织

文章目录 0x01 什么是紫队0x02 如何组织攻防实战攻防演习一、实战攻防演习组织要素二、实战攻防演习组织形式三、实战攻防演习组织关键 摘抄 0x01 什么是紫队 ● 紫队&#xff0c;一般是指网络实战攻防演习中的组织方。 ● 紫队是在实战攻防演习中&#xff0c;以组织方角色&am…
阅读更多...
java毕业设计民兵管理系统（附源码、数据库）

java毕业设计民兵管理系统（附源码、数据库）

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat8.5 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; Springboot mybatis Maven Vue 等等组成&#xff0c;B/…
阅读更多...
哨兵数据的介绍

哨兵数据的介绍

转载&#xff1a;[哨兵数据的介绍(http://www.spacemagazines.org/h-nd-193.html) “哨兵”卫星家族概览 据欧洲航天局网站2014年5月28日的报道&#xff0c;欧洲哨兵&#xff0d;1A&#xff08;Sentinel&#xff0d;1A&#xff09;卫星尽管还没有正式工作&#xff0c;但已为波…
阅读更多...
创建Dota游戏中的兵营类（Barrack），创建3个兵营，通过控制台为每个兵营定义兵营名称，并指定该兵营需要创建的士兵人数。

创建Dota游戏中的兵营类（Barrack），创建3个兵营，通过控制台为每个兵营定义兵营名称，并指定该兵营需要创建的士兵人数。

上面图标里的这个类是创建的兵营类,下面的代码是兵营类的测试类: package com.xjc; /任务一&#xff0c; 1.创建Dota游戏中的兵营类&#xff08;Barrack&#xff09;&#xff0c;该类中有一个类成员变量count&#xff08;类属性&#xff09;、一个实例变量name和另一个实例变…
阅读更多...
敌兵布阵问题

敌兵布阵问题

一 问题描述 A 国在海岸线沿直线部署了 N 个工兵营地&#xff0c;C 国通过先进的监测手段&#xff0c;对 A 国的每个工兵营里的人数都掌握的一清二楚&#xff0c;每个工兵营的人数都可能发生变动&#xff0c;可能增加或减少若干人数。 二 输入和输出 1 输入 第 1 行包含一个…
阅读更多...
红蓝对抗-红队打点的那些事

红蓝对抗-红队打点的那些事

红蓝对抗-红队打点的那些事 攻防演练中作为攻击方&#xff0c;效率很重要&#xff0c;例如2019 BCS红队行动议题&#xff1a; RedTeam-BCS 半自动化的资产收集 域名/IP/需要交互的系统 当拿到目标的时候&#xff0c;首先需要利用天眼查获取目标企业结构&#xff0c;有子公司…
阅读更多...
如何快速搭建红队练习靶场

如何快速搭建红队练习靶场

使用项目：Vulhub Vulhub是一个基于docker和docker-compose的漏洞环境集合，进入对应目录并执行一条语句即可启动一个全新的漏洞环境，让漏洞复现变得更加简单，让安全研究者更加专注于漏洞原理本身。 前期准备 安装docker curl -s https://get.docker.com/ | sh
阅读更多...
UGC、PGC、OGC比较详解

UGC、PGC、OGC比较详解

UGC、OGC 和 PGC &#xff0c;是网络平台上三种常见的内容生产模式&#xff0c;本文主要对其差别进行比较。 UGC模式 UGC&#xff08;全称为 User Generated Content&#xff0c;即用户输出内容&#xff09; 主要是通过激励用户生产内容&#xff0c;形成社区氛围。 UGC模式…
阅读更多...
OGC服务接口一张图

OGC服务接口一张图

阅读更多...
【学习心得】OGC城市地理标记语言（CityGML）编码标准_CityGML一般性特征

【学习心得】OGC城市地理标记语言（CityGML）编码标准_CityGML一般性特征

CityGML概述 CityGML是一种基于XML格式的、用于存储和交换虚拟3D城市模型的开放数据模型。它是地理标记语言3.1.1版 本(GML3)的一个应用模式&#xff0c;是由OGC和ISO TC211发布的用于空间数据交换的可扩展国际标准 开发CityGML的目标是为了对三维城市模型的基本实体、属性和…
阅读更多...
UGC、PGC、OGC概念、例子和关联和区别

UGC、PGC、OGC概念、例子和关联和区别

https://www.jianshu.com/p/c02881007758 概念&例子&#xff1a; UGC: User-generated Content 用户生产内容。是指用户将自己原创的内容通过互联网进行展示或者给其他用户。它是一种以Web2.0概念而新兴的方式&#xff0c;现在由原来的以下载为主变成下载和上传并重。 …
阅读更多...
推荐文章

Copyright @ 2022~2023