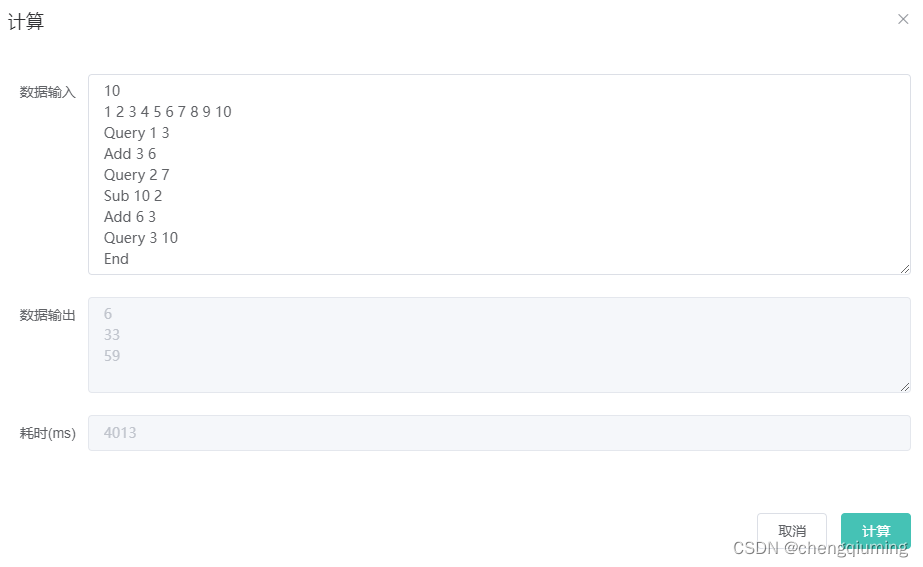
第二题:B - 切绳子
题目如下图所示:


这道题目难度中等,但是有很多细节要注意。
分析:
1.首先数据类型问题, 1<n<1e18,这个显然超过了int的长度65535,需要使用big int 或者是long long 型进行定义变量,才不会报错。
2.包含 T 组数据,意味着需要处理多个,那么对存储空间就有要求,不能将每切一次的数据都保存,否则可能会存储超限。
3.每切一次,会分成[m/2],n-[m/2],那么只需要取其中长的那一段,一定是这两段中需要切的次数最多的,以此可以简化程序。
4.考虑使用迭代的方法,定义一个子函数作为切割绳子的处理,只需要返回处理的次数(即天数)。
思路:
- 这道题一开始的时候,我的思路是使用二叉树进行分割,左孩子为n-[m/2],右孩子为[m/2],这样交换的好处是可以构成一个完全二叉树(!注意不是满二叉树,除非绳子长度恰好是2^n,才会刚好构成满二叉树)。一直分下去,直到结点的值为1,构成叶结点,那么这颗二叉树的深度就是剪绳子需要的天数。但是这个想法由于水平不够,我没能想出实现的程序。因此考虑了第二种更为直接的思路。
- 第二种思路,是基于这个问题的数学表达式,抽象为数学问题,就是把一个数n不断地除以2,取整。那么我们想,2^n 这个数需要n次除法得到1,2 ^(n+1)这个数需要n+1次除法得到1,那么在这两个数之间的数字,得到1所需要的除法次数一定是在[n,n+1]内的,那么按题目所给的信息,除法后取整,这个次数必然是一个整数,那么只能是n+1。可以举例来验证这个思路:如 2 ^3=8,2 ^ 4=16,那么12需要几次呢,
12-> 6 -> 3 -> 2 ->1 ,一共是4次,即12需要4次才能全部变成1 ,这里面只需要取两个数中最大的那个进行下一次剪操作。
因此,思路简化为,比较绳子长度与2^ n进行比较,返回第一个比绳子长度大的2 ^n 的 n值。考虑边界,当绳子长度为1,不需要剪,因此n应该从0开始比较。
求解代码如下:
// 第二题:B - 切绳子
#include <queue>
#include <vector>
#include <cmath>
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<math.h>
using namespace std;int Getday(long long n)
{int day =1;while(n>1){long long m = n/2;n = max(m,n-m);day++;}return day;
}int main()
{int T;cin >> T;vector<int>res;long long n;for (int i = 0; i < T; i++){cin >> n;int day = Getday(n);res.push_back(day);}for (int i = 0; i < T; i++)cout << res[i] << endl;return 0;
}