在前期推送的内容中,我们介绍了构建多因素回归模型,探讨对结局指标有独立作用的影响因素,就好比侦探破案找出真凶的过程。我们作为研究人员,就像是一名侦探,通过统计学方法及专业知识,在众多的嫌疑人中一一排查,来一次『白夜追凶』,最终才能找出真正的凶手X。
相关阅读:嫌疑人X的献身:如何理解回归模型中的"调整"和"独立作用"
当然,要做一名好侦探,你一定要有一种可靠的直觉,能够准确划定嫌疑人的范围,这才是成功破案最为关键的一步,如果事先连嫌疑人都判断错了,那就只能让凶手逃之夭夭了。
同样,对于一个研究来说,我们通常会收集很多数据资料,但由于受到样本量、或者结局事件数量的限制,我们不可能把所有的变量都带入到多因素回归中进行分析。那么,在面对众多自变量需要进行分析时,到底如何来确定谁是可疑因素,哪些因素需要被纳入到嫌疑人的范围内,从而进入到多因素回归分析呢?今天就跟着小咖一起,教大家如何筛选多因素回归分析的候选变量。
研究实例
学习标准的统计方法,最直观便捷的一个途径就是从文献中去学习,看看在高分期刊上发表文章的大牛们都是怎么进行分析的。
我们首先来看一篇2011年发表在The New England Journal of Medicine (影响因子:72.4)的文章:《A Prospective Natural-History Study of Coronary Atherosclerosis》[1]。
我们先不管这篇文章都做了哪方面的研究,就单凭作者对于统计学方法的描述,小咖觉得已经足够膜拜的了。
关于如何筛选多因素回归分析的候选变量,作者原文中这样写道:
Baseline variables that were considered clinically relevant or that showed a univariate relationship with outcome were entered into multivariate Cox proportional-hazards regression model. Variables for inclusion were carefully chosen, given the number of events available, to ensure parsimony of the final model.
小咖觉得这句话写的实在是太经典了,有需要的小伙伴可以先把它收藏起来,作为一个模板以后用在自己的文章里。这句话很精炼地概括出了在多因素回归分析中进行变量筛选时需要满足的几个基本条件:
1. Clinical Relevant
作为对结局事件有影响的候选变量,首先从临床专业知识的角度考虑,它的作用一定是被人们可接受的,可以从某个生理机制或途径去进行合理的解释。我们常见的候选变量包括以下几类:
(1) 人口学资料:例如性别、年龄、学历、职业、身高、体重等
(2) 生活习惯:例如吸烟、饮酒、体育锻炼等
(3) 病史信息:例如家族史、既往史(高血压、糖尿病、心梗等)等
(4) 检查信息:例如血液指标(LDL-C、CRP)、其他检查项目等
(5) 治疗信息:例如用药、手术等
(6) 暴露/处理因素
针对以上很多候选变量无从下手时,我们可以参考既往发表的文献,总结出已公开发表报道过的对结局事件有独立作用的变量,将它们作为重点的候选变量以供备选。
2. Univariate relationship with outcome
第二个筛选变量的角度是从单因素分析的结果入手。我们在前几期推送的文章中,已经讨论过了传统单因素分析和单因素回归分析的关系,以及单因素分析和多因素分析的关系。
需要复习的同学可以戳这里:
- 搞懂传统单因素分析和单因素回归分析的纠葛,有这篇文章就够了!
- 单因素分析和多因素分析的结果不一致,怎么办?
其中提到单因素分析的结果可以作为我们多因素分析的一个参考,也就是说通过单因素分析的结果,可以帮助我们来判断哪些因素是对结局事件有影响的可疑因素,从而将其作为多因素分析的候选变量。
我们再来看一篇文章,2013年发表在JACC杂志(影响因子:19.9)上的文章《Predictors for Functionally Significant In-Stent Restenosis》[2]。
作者在统计方法中这样写道:
Candidate variables with a p value <0.2 on univariate analysis were included in multivariable model.
由于在单因素分析中,其结果之间的差异并不能很真实得反映出该因素对结局事件的效应,我们可以将单因素分析结果有统计学显著性的变量(P<0.05),作为候选变量的第一梯队。
当然,我们也可以适当地将纳入标准放宽到P<0.1,或者P<0.2,甚至有的研究放宽到P<0.25,这样可以有效地避免遗漏一些重要变量。虽然它们在单因素分析中无统计学显著性,但其真实的效应有可能被低估或者被掩盖,这样可以尽可能多地纳入可疑的混杂因素放入模型中进行调整。
3. Given the number of events available
当然,在多因素回归分析中纳入的变量并非越多越好,我们还要从模型的稳健程度去考虑。
我们前期推送的这篇文章:
- 说到控制混杂因素,怎么能不提多因素分析!咋筛选变量进入多因素回归
文中已经提到控制混杂因素的个数主要取决于发生结局事件的多少,控制的混杂因素越多,所需要的结局事件的例数就越多。对于多重线性回归模型,样本量应至少为10-15的自变量个数,而对于logistic回归和Cox回归,结局事件则应至少为15-20倍的自变量个数。
也就是说,如果你打算做多重线性回归,想要在模型中纳入10个变量,那就要求样本量至少为100-150个;如果你准备做logistic或Cox回归,想要在模型中纳入10个变量,那么要求所需要的结局事件至少为150-200个。
需要注意的是,这里指的是结局事件的数量,而不是总的样本量,总样本量当然还要远远多于结局事件的数量。
分析步骤
好了,我们来总结一下这种变量筛选方法的分析套路:
第一步:单因素分析,对研究对象的基线资料进行比较;
第二步:筛选变量,需要考虑上述几点:
(1) 统计学有显著性,P<0.05,但此时P值已经并不十分重要,可以将P值放宽到0.1甚至0.2;
(2) 统计学上无显著性,但有临床意义,或者前期文献报道过有意义的变量;
(3) 结合自己的样本量或结局事件的数量,确定适宜的候选变量数量。
第三步:多因素回归分析,对模型参数进行解释。
结合我们前期推送的文章《说到控制混杂因素,怎么能不提多因素分析!》,对于观察性研究,我们常常要通过构建多因素回归模型,控制混杂因素的影响,从而探索暴露/处理因素的独立效应。
今天的内容我们就具体介绍了如何在多因素分析中进行变量筛选,这是我们最常用到的简单易行的方法,相信大家在平时自己分析数据的时候也会多多少少用到这种方法。但上述方法在筛选变量的时候,最主要的还是要看单因素分析的P值,由P值来主导自变量的去留。
不过如果组间各因素在基线状态下较为均衡,单因素分析结果并无显著差异,那么仅从单因素分析的P值并不能给我们提供太多的信息。而且近几年来统计学家们也呼吁大家不要太过于看重P值的地位,仔细想一想那些P>0.2的变量,它们就真的与结局事件无关了么?
所以,如果你以为筛选变量就这么简单,那就小看统计学的魅力了。对于在多因素回归分析中进行变量筛选的进阶方法,我们会在下期内容中继续向大家进行介绍。
相信许多小伙伴们在做多因素回归时候总是看文献的做法,先进行一次单因素回归,然后将单因素回归的有意义的指标纳入多因素回归中,简直就是无脑纳入,只要有意义,全部纳入,而无异议的看都不看就直接扔了,其实这样是不对的,但是这对于你发表论文可能没什么影响,因为很多审稿人根本就不知道多因素回归,(包括多因素logistics回归以及多因素cox回归)的具体定义,也不知道其纳入方法,外国人更是傻傻分不清楚了,但是说归说,我们还是要从本质去学习,了解什么是真理,什么是目的,目的是需要手段去实现的,但是真理才是永恒的。这里重要的一点是单纯纳入单因素分析中有意义的指标进入多因素分析,结果是不靠谱的,因为你很可能将重要的影响因素排除在外!!
举个例子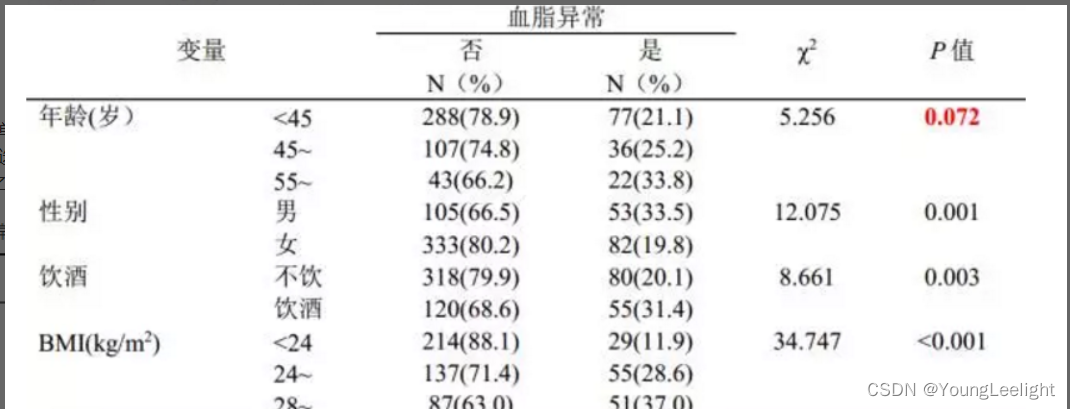
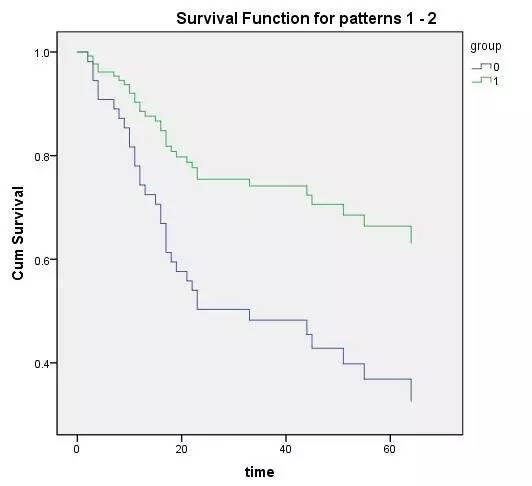
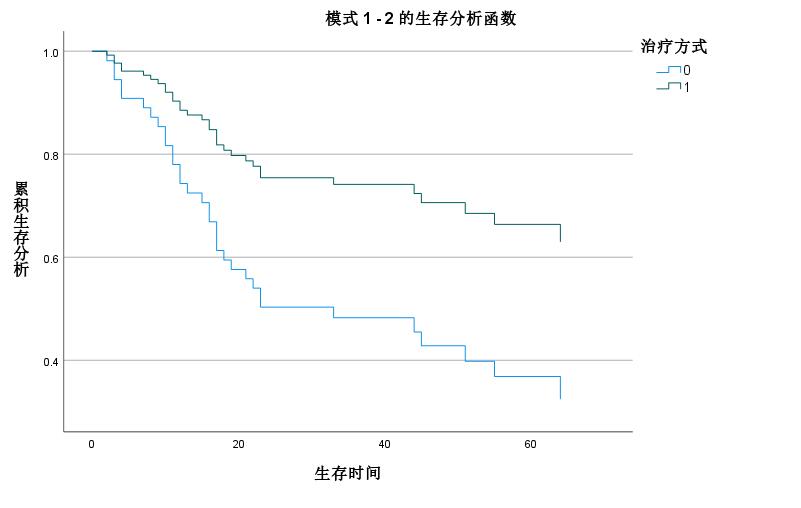
这里显然在单因素回归中(此处为单因素logistics回归)年龄是无意义的,但是地球人用脚趾头想想都能知道血脂的异常跟年龄是显著有关的啊,
这里先别着急将年龄从血脂异常候选影响因素中删去,我们再来看看多因素Logistic回归分析结果。SPSS软件的多因素Logistic回归结果显示,55-岁组血脂异常的患病风险是<45岁组的2.093倍。之所以会出现这种现象,是因为在做单因素分析时,往往无法识别混杂因素的存在,而混杂因素很可能会干扰我们关注的变量与结局之间的关系。
请仔细看这里的解释,55-岁组血脂异常的患病风险是<45岁组的2.093倍(我们并没有说45-55岁之间的人怎么怎么样,因为他p值没意义,so这里的描述要追求真理的情况下,显然需要更加细化的描述,就跟前面蓝字一样的描述,如果你傻傻分不清,论文是初级选手,或者不想写那么细化的论文,想简单点,请参照下图将年龄划出去就行
就是这里,不要将年龄这个变量纳入分类变量,那么就能显示出你想要的结果)
所以,如果多因素Logistic回归分析时,只纳入单因素分析有统计学意义的自变量,则有时候某些影响因素就没有机会进入多因素模型(比如栗子中的年龄,而年龄确实对血脂异常有影响)。
因此,采用单因素分析进行影响因素的筛选时,应注意适当调整检验水平(P<0.05并不是万能的,影响因素的探索性分析可以适当放开检验水准,比如设定为α=0.10 or 0.15),并结合临床专业(变量与结局之间的关系临床上是否讲得通),选择纳入多因素分析的变量,不要一味地舍弃单因素分析无统计学意义的自变量,要避免漏掉重要的影响因素
一个更好的方法是使用LASSO(LeastAbsolute Shrinkage and Selection Operator)法来构建模型,这种方法一方面惩罚回归系数的绝对值大小进而实现选择变量(Selection),另一方面降低极端变量的权重(Shrinkage)。
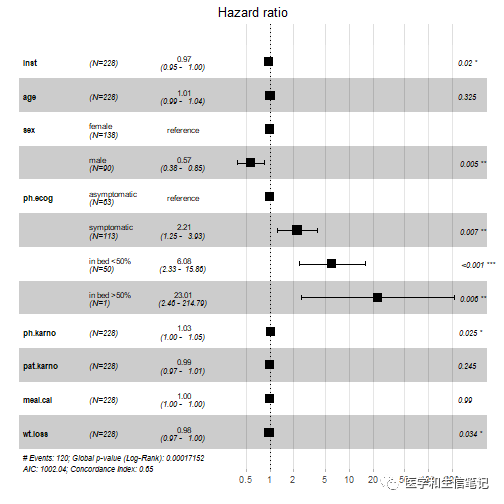
图展示了GOF图,使用的是Cox回归模型。预测变量的任何组合中,很明显年龄是最强的因素,包括年龄的模型是最好的,包括BMI但不包括年龄的模型一般是最糟糕的。因此,最好的多因素模型是不包含BMI的其他所有变量的模型。然而,需要明确的是BMI仍然是一个重要的预测因素,比如说,BMI测量比较方便,但是血脂却不方便测量,我们可以考虑用BMI替代血脂
从图2不难看出,GOF图有一个明显的缺点——制作太耗费时间,这才7个变量就有128种组合,如果更多变量呢?相信很多小伙伴头都要大了,但是不可否认,目前我们的研究中变量相对还较少,借助统计软件,GOF图还是比较实用
3. 除了上述的两个方面外,还需要考虑变量之间是否存在交互。如果交互确实存在,那么变量的交互项也需要纳入到预测模型中。当然还有一个比较简单的解决方案,就是分层拟合预测模型。举个栗子,ASSIGN评分对于不同性别就有独立的风险评分()。
总之,变量筛选需要结合临床专业判断和统计学方法,才能选出最好的模型!
注:本文中用的图有一部分是logistics回归,一部分我有点偷懒,所以用了原有数据的cox回归,其实两个回归之间的差别就是最终你观测的变量cox回归是时间连续变量,而logistics回归是二分类变量或者多分类变量罢了。原理都一样
|
|