激光SLAM
帧间匹配方法:
- Point-to-Plane ICP
- NDT
- Feature-based Method
回环检测方法:
- Scan-to-Scan
- Scan-to-Map
LOAM创新点
- 定位和建图的分离:
- 里程计模块:高频低质量的帧间运动估计
- 建图模块:低频高质量的用于点云的精细匹配和配准
- 基于特征的帧间匹配
- 提取边缘特征点(edge)和平面特征点(plannar)
激光雷达里程计
特征点提取
第k次扫描(sweep)的点云表示为 P k \mathcal{P}_k Pk,其中一个扫描点 i ∈ P k i\in\mathcal{P}_k i∈Pk,令 S i \mathcal{S}_i Si表示同一扫描中点i周围的点集,点i的曲率:
c i = 1 ∣ S ∣ ∥ X ( k , i ) L ∥ ∥ ∑ j ∈ S , j ≠ i ( X ( k , i ) L − X ( k , j ) L ) ∥ ( 1 ) c_i=\frac{1}{|\mathcal{S}|\lVert X_{\left( k,i \right)}^{L} \rVert}\lVert \sum_{j\in \mathcal{S},j\ne i}{\left( X_{\left( k,i \right)}^{L}-X_{\left( k,j \right)}^{L} \right)} \rVert \qquad\qquad(1) ci=∣S∣∥X(k,i)L∥1∥j∈S,j=i∑(X(k,i)L−X(k,j)L)∥(1)
根据曲率值对一次扫描中的点进行排序,选取曲率最大的点为边缘特征点(edge point),选取曲率最小的点为平面特征点(plannar point)。边缘特征点的曲率需要大于某个阈值,平面特征点的曲率需要小于某个阈值。已经被选择的特征点附近的点不再考虑,选择的特征点总量也有限制。
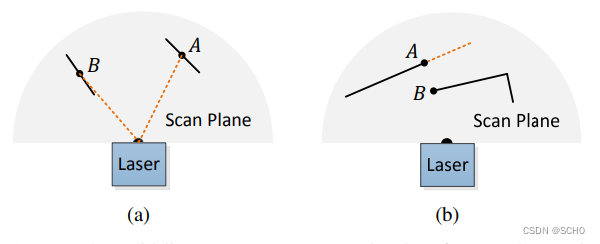
另外,还需要排除一些异常值:
1)排除平行于激光扫描平面的点,候选点及其附近点集合拟合的平面与激光线束的夹角不能过小,对应(a);
2)排除遮挡区域边界的点,候选点附近的点集中没有与候选点在激光束方向上间距过大的点,对应(b)。

特征匹配
基于特征的Scan-to-Scan匹配方法
在开始于 t k t_k tk的第k次sweep扫描完成之后, P k \mathcal{P}_k Pk被重投影到时刻 t k + 1 t_{k+1} tk+1,记作 P ˉ k \bar{\mathcal{P}}_k Pˉk,并存储在3D KD-tree中用于快速检索,以方便之后的匹配。

在第k+1次sweep扫描开始后, P k + 1 \mathcal{P}_{k+1} Pk+1随着接收到更多的点而逐渐增长,按照上一章的提取方法提取边缘特征点和平面特征点。令 E k + 1 \mathcal{E}_{k+1} Ek+1和 H k + 1 \mathcal{H}_{k+1} Hk+1分别表示k+1次sweep边缘特征点和平面特征点的集合。从 P ˉ k \bar{\mathcal{P}}_k Pˉk中找到边缘线作为 E k + 1 \mathcal{E}_{k+1} Ek+1中点的对应,平面块作为 H k + 1 \mathcal{H}_{k+1} Hk+1中点的对应。
激光里程计在一次扫描过程中迭代估计自身运动,在每次迭代中,使用当前估计的变换将将 E k + 1 \mathcal{E}_{k+1} Ek+1和 H k + 1 \mathcal{H}_{k+1} Hk+1重投影到扫描开始时刻,记为 E ~ k + 1 \tilde{\mathcal{E}}_{k+1} E~k+1和 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1。
下图左侧表示寻找边缘点的对应边缘线的过程,设i为 E ~ k + 1 \tilde{\mathcal{E}}_{k+1} E~k+1中的一个点, i ∈ E ~ k + 1 i\in \tilde{\mathcal{E}}_{k+1} i∈E~k+1,边缘线由两个点表示。设j是i在 P ˉ k \bar{\mathcal{P}}_k Pˉk中的最近邻点,l是i在j的相邻线束扫描中的最近邻点。(j,l)构成了i的对应边缘线。然后需要根据曲率式(1)验证j和l都是边缘点。这样做的考虑是单个扫描线不能包含来自同一边缘线的多个点,只有一个例外:边缘线平行于扫描平面,这种情况是异常情况不会提取特征点。
下图右侧表示寻找平面点的对应平面块,与边缘点类似,在 P ˉ k \bar{\mathcal{P}}_k Pˉk中找i的最近邻点j。然后在j的相同扫描线和相邻扫描线中分别找i的最近邻点l和m,这保证了三个点不共线。然后根据曲率公式验证是平面点。

点到线的距离:
d E = ∣ ( X ~ ( k + 1 , i ) L − X ˉ ( k , j ) L ) × ( X ~ ( k + 1 , i ) L − X ˉ ( k , l ) L ) ∣ ∣ X ~ ( k + 1 , i ) L − X ˉ ( k , l ) L ∣ d_{\mathcal{E}}=\dfrac{\left\lvert \left(\tilde{\boldsymbol{X}}^L_{(k+1,i)}-\bar{\boldsymbol{X}}^L_{(k,j)}\right) \times \left(\tilde{\boldsymbol{X}}^L_{(k+1,i)}-\bar{\boldsymbol{X}}^L_{(k,l)}\right)\right\rvert}{\left\lvert\tilde{\boldsymbol{X}}^L_{(k+1,i)}-\bar{\boldsymbol{X}}^L_{(k,l)}\right\rvert} dE=∣ ∣X~(k+1,i)L−Xˉ(k,l)L∣ ∣∣ ∣(X~(k+1,i)L−Xˉ(k,j)L)×(X~(k+1,i)L−Xˉ(k,l)L)∣ ∣
点到面的距离:
d H = ∣ ( X ~ ( k + 1 , i ) L − X ˉ ( k , j ) L ) ⋅ ( X ˉ ( k , j ) L − X ˉ ( k , l ) L ) × ( X ˉ ( k , j ) L − X ˉ ( k , m ) L ) ∣ ∣ ( X ˉ ( k , j ) L − X ˉ ( k , l ) L ) × ( X ˉ ( k , j ) L − X ˉ ( k , m ) L ) ∣ d_{\mathcal{H}}=\dfrac{\left\lvert \left(\tilde{\boldsymbol{X}}^L_{(k+1,i)}-\bar{\boldsymbol{X}}^L_{(k,j)} \right) \cdot \left(\bar{\boldsymbol{X}}^L_{(k,j)}-\bar{\boldsymbol{X}}^L_{(k,l)}\right) \times \left(\bar{\boldsymbol{X}}^L_{(k,j)}-\bar{\boldsymbol{X}}^L_{(k,m)}\right)\right\rvert}{\left\lvert \left(\bar{\boldsymbol{X}}^L_{(k,j)}-\bar{\boldsymbol{X}}^L_{(k,l)}\right) \times \left(\bar{\boldsymbol{X}}^L_{(k,j)}-\bar{\boldsymbol{X}}^L_{(k,m)}\right)\right\rvert} dH=∣ ∣(Xˉ(k,j)L−Xˉ(k,l)L)×(Xˉ(k,j)L−Xˉ(k,m)L)∣ ∣∣ ∣(X~(k+1,i)L−Xˉ(k,j)L)⋅(Xˉ(k,j)L−Xˉ(k,l)L)×(Xˉ(k,j)L−Xˉ(k,m)L)∣ ∣
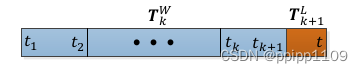
令 T k + 1 L \boldsymbol{T}^L_{k+1} Tk+1L代表 t k + 1 t_{k+1} tk+1到 t t t的雷达位姿变换
点-线残差:
f E ( X ( k + 1 , i ) L , T k + 1 L ) = d E , i ∈ E k + 1 f_{\mathcal{E}}(\boldsymbol{X}^L_{(k+1,i)},\boldsymbol{T}^L_{k+1})=d_{\mathcal{E}}\ ,\ i\in\mathcal{E}_{k+1} fE(X(k+1,i)L,Tk+1L)=dE , i∈Ek+1
点-面残差:
f H ( X ( k + 1 , i ) L , T k + 1 L ) = d H , i ∈ H k + 1 f_{\mathcal{H}}(\boldsymbol{X}^L_{(k+1,i)},\boldsymbol{T}^L_{k+1})=d_{\mathcal{H}}\ ,\ i\in\mathcal{H}_{k+1} fH(X(k+1,i)L,Tk+1L)=dH , i∈Hk+1
将所有点-线残差和点-面残差结合起来得到残差矢量
f ( T k + 1 L ) = d \boldsymbol{f}(\boldsymbol{T}^L_{k+1})=\boldsymbol{d} f(Tk+1L)=d
最小二乘问题:
min T k + 1 L F ( x ) = 1 2 ∥ f ( T k + 1 L ) ∥ Ω 2 \min_{\boldsymbol{T}^L_{k+1}} F(x)=\dfrac{1}{2} \left\lVert \boldsymbol{f}(\boldsymbol{T}^L_{k+1}) \right\rVert^2_{\Omega} Tk+1LminF(x)=21∥ ∥f(Tk+1L)∥ ∥Ω2
其中 ∥ x ∥ Ω 2 = x T Ω x \left\lVert \boldsymbol{x}\right\rVert_{\Omega}^2=\boldsymbol{x}^T\Omega \boldsymbol{x} ∥x∥Ω2=xTΩx, Ω \Omega Ω是权重矩阵,又叫信息矩阵。
该算法为每个特征点分配一个二方权重。与其对应的距离较大的特征点被分配较小的权重,距离大于阈值的特征点被认为是异常值并分配零权重。