SciPy简单应用
SciPy是在NumPy的基础上增加了大量用于数学计算,科学计算以及工程计算的模块,包括线性代数,常微分方程求解,信号处理,图像处理于稀疏矩阵等。参考文档
目录
- SciPy简单应用
- 文件输入/输出:scipy.io
- 特殊函数:scipy.special
- 线性代数操作:scipy.linalg
- 优化及拟合:scipy.optimize
- 统计和随机数:scipy.stats
SciPy主要模块如下表:
| 模块 | 说明 |
|---|---|
scipy.cluster | 向量计算 / Kmeans |
scipy.constants | 物理和数学常量 |
scipy.fftpack | 傅里叶变换 |
scipy.integrate | 积分程序 |
scipy.interpolate | 插值 |
scipy.io | 数据输入和输出 |
scipy.linalg | 线性代数程序 |
scipy.ndimage | n-维图像包 |
scipy.odr | 正交距离回归 |
scipy.optimize | 优化 |
scipy.signal | 信号处理 |
scipy.sparse | 稀疏矩阵 |
scipy.spatial | 空间数据结构和算法 |
scipy.special | 一些特殊数学函数 |
scipy.stats | 统计 |
他们全都依赖于numpy, 但是大多数是彼此独立的。导入Numpy和Scipy的标准方式:
import numpy as np
from scipy import stats # 其他的子模块类似
文件输入/输出:scipy.io
- 载入和保存matlab文件:
from scipy import io as spio
a = np.ones((3, 3))
spio.savemat('file.mat', {'a': a}) # savemat expects a dictionary
data = spio.loadmat('file.mat', struct_as_record=True)
data['a']
array([[1., 1., 1.],[1., 1., 1.],[1., 1., 1.]])
- 载入文本文件
numpy.loadtxt(fname, dtype=<class 'float'>, comments='#', delimiter=None, converters=None, skiprows=0, usecols=None, unpack=False, ndmin=0, encoding='bytes', max_rows=None)
from io import StringIO # StringIO behaves like a file object
import numpy as np
c = StringIO(u"0 1\n2 3")
print(np.loadtxt(c))
[[0. 1.][2. 3.]]
d = StringIO(u"M 21 72\nF 35 58")
np.loadtxt(d, dtype={'names': ('gender', 'age', 'weight'), # dtype指定解析出来的数据类型'formats': ('S1', 'i4', 'f4')})
array([(b'M', 21, 72.), (b'F', 35, 58.)],dtype=[('gender', 'S1'), ('age', '<i4'), ('weight', '<f4')])
c = StringIO(u"1,0,2\n3,0,4")
"""
delimiter指定文件中数据之间的分隔符
usecols 指定读取文件中的哪些列,在下面的函数中,usecols=(0,2)表示只读取文件的第1、3列
unpack:读出来的数据是否需要解包,注意接受函数的变量个数要与读出来的行数或列数吻合
"""
x, y = np.loadtxt(c, delimiter=',', usecols=(0, 2), unpack=True)
x
array([1., 3.])
y
array([2., 4.])
特殊函数:scipy.special
常用的一些函数如下:
- 贝塞尔函数,比如scipy.special.jn() (第n个整型顺序的贝塞尔函数)
- 椭圆函数 (scipy.special.ellipj() Jacobian椭圆函数, …)
- Gamma 函数: scipy.special.gamma(), 也要注意 scipy.special.gammaln() 将给出更高准确数值的 Gamma的log。
- Erf, 高斯曲线的面积:scipy.special.erf(),也叫误差函数
线性代数操作:scipy.linalg
- scipy.linalg.det() 函数计算方阵的行列式:
from scipy import linalg
arr = np.array([[1, 2],[3, 4]])
linalg.det(arr)
-2.0
arr = np.array([[3, 2],[6, 4]])
linalg.det(arr) # 科学计数法 6.661338147750939e-16 =6.661338147750939 x 10^-16 约等于0
6.661338147750939e-16
- scipy.linalg.inv() 函数计算逆方阵
arr = np.array([[1, 2],[3, 4]])
iarr = linalg.inv(arr)
iarr
array([[-2. , 1. ],[ 1.5, -0.5]])
np.allclose(np.dot(arr, iarr), np.eye(2)) # numpy的allclose方法,比较两个array是不是每一元素都相等,默认在1e-05的误差范围内
True
计算行列式为0的矩阵将抛出LinAlgError :
arr = np.array([[3, 2],[6, 4]])
linalg.inv(arr)
---------------------------------------------------------------------------LinAlgError Traceback (most recent call last)<ipython-input-20-a62c7b607b7e> in <module>1 arr = np.array([[3, 2],2 [6, 4]])
----> 3 linalg.inv(arr)~\Anaconda3\envs\tf2\lib\site-packages\scipy\linalg\basic.py in inv(a, overwrite_a, check_finite)972 inv_a, info = getri(lu, piv, lwork=lwork, overwrite_lu=1)973 if info > 0:
--> 974 raise LinAlgError("singular matrix")975 if info < 0:976 raise ValueError('illegal value in %d-th argument of internal 'LinAlgError: singular matrix
- 奇异值分解(SVD)
A = U Σ V T A=U\varSigma V^T A=UΣVT
arr = np.arange(9).reshape((3, 3)) + np.diag([1, 0, 1])
print(arr)
uarr, spec, vharr = linalg.svd(arr)
[[1 1 2][3 4 5][6 7 9]]
结果的数组频谱(矩阵的特征值$\lambda $组成的对角阵)是:
spec
array([14.88982544, 0.45294236, 0.29654967])
U矩阵为:
uarr
array([[-0.1617463 , -0.98659196, 0.02178164],[-0.47456365, 0.09711667, 0.87484724],[-0.86523261, 0.13116653, -0.48390895]])
V矩阵为:
vharr
array([[-0.45513179, -0.54511245, -0.70406496],[ 0.20258033, 0.70658087, -0.67801525],[-0.86707339, 0.45121601, 0.21115836]])
根据公式,我们可以根据UV矩阵和特征值矩阵还原原始矩阵
sarr = np.diag(spec) # 将spec矩阵化为对角阵
svt_mat = uarr.dot(sarr).dot(vharr)
print(svt_mat)
[[1. 1. 2.][3. 4. 5.][6. 7. 9.]]
- 快速傅立叶变换:scipy.fftpack
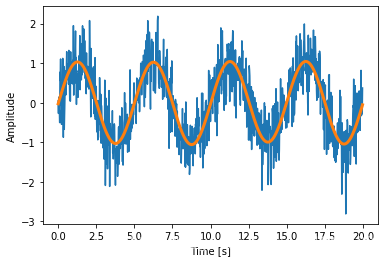
假设一个(有噪音)的信号输入是这样:
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)# sin(wt+n)
sig = np.sin(2 * np.pi / period * time_vec) + \0.5 * np.random.randn(time_vec.size)
假设信号来自真实的函数,因此傅立叶变换将是对称的。scipy.fftpack.fftfreq() 函数将生成样本序列,而将计算快速傅立叶变换:
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d=time_step) # 通过DFFT生成样本序列
sig_fft = fftpack.fft(sig)
因为生成的幂是对称的,寻找频率只需要使用频谱为正的部分:
pidxs = np.where(sample_freq > 0)
freqs = sample_freq[pidxs]
power = np.abs(sig_fft)[pidxs]
寻找信号频率:
freq = freqs[power.argmax()] # 频谱中功率的最高点就是信号的原始频率
np.allclose(freq, 1./period) # 检查是否找到了正确的频率
True
现在高频噪音将从傅立叶转换过的信号移除:
sig_fft[np.abs(sample_freq) > freq] = 0
生成的过滤过的信号可以用scipy.fftpack.ifft()函数做傅里叶逆变换:
main_sig = fftpack.ifft(sig_fft)
查看结果:
plt.figure()
plt.plot(time_vec, sig )
plt.plot(time_vec, np.real(main_sig), linewidth=3 )
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.show()
优化及拟合:scipy.optimize
- 寻找标量函数的最小值
from scipy import optimize
让我们定义下面的函数:
def f(x):return x**2 + 10*np.sin(x)x = np.arange(-10, 10, 0.1)
plt.plot(x, f(x))
plt.show()
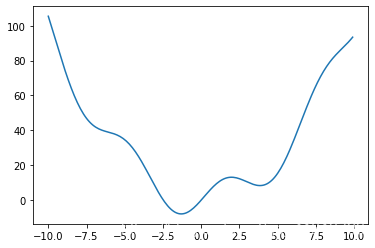
这个函数在-1.3附近有一个全局最小并且在3.8有一个局部最小。
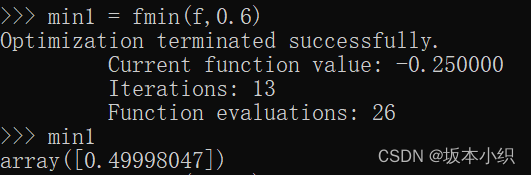
找到这个函数的最小值的常用有效方式是从给定的初始点开始进行一个梯度下降。BFGS算法是这样做的较好方式:
optimize.fmin_bfgs(f, 0)
Optimization terminated successfully.Current function value: -7.945823Iterations: 5Function evaluations: 18Gradient evaluations: 6array([-1.30644012])
这个方法的一个可能问题是,如果这个函数有一些局部最低点,算法可能找到这些局部最低点而不是全局最低点,这取决于初始点:
optimize.fmin_bfgs(f, 3, disp=0) # 将起点设置为3,无法找到全局最低点
array([3.83746709])
如果我们不知道全局最低点,并且使用其临近点来作为初始点,那么我们需要付出昂贵的代价来获得全局最优。要找到全局最优点,最简单的算法是暴力算法,算法中会评估给定网格内的每一个点:
grid = (-10, 10, 0.1)
xmin_global = optimize.brute(f, (grid,))
xmin_global
array([-1.30641113])
- 寻找标量函数的根scipy.optimize.fsolve():
要寻找上面函数f的根,比如f(x)=0的一个点
root = optimize.fsolve(f, 1) # 我们的最初猜想是1
root
array([0.])
注意只找到一个根。检查f的图发现在-2.5左右还有应该有第二个根。通过调整我们最初的猜想,我们可以发现正确的值:
root2 = optimize.fsolve(f, -2.5)
root2
array([-2.47948183])
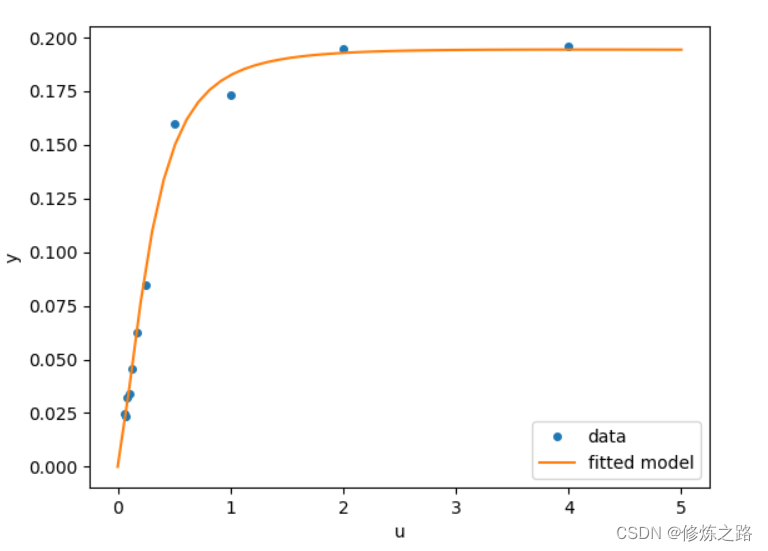
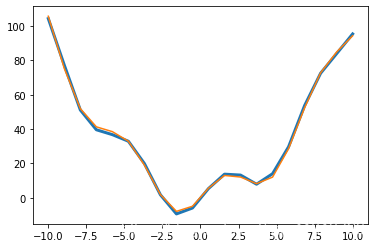
- 曲线拟合
假设我们有来自f的样例数据,带有一些噪音:
y=h(t) * x(t)+n(t)
xdata = np.linspace(-10, 10, num=20)
ydata = f(xdata) + np.random.randn(xdata.size) # 第二项为噪音
现在,如果我们知道这些sample数据来自的函数(这个案例中是 x 2 + s i n ( x ) x^2 + sin(x) x2+sin(x))的函数形式,而不知道每个数据项的系数,那么我们可以用最小二乘曲线拟合在找到这些系数。首先,我们需要定义函数来拟合:
def f2(x, a, b): # a,b为拟合参数,即x^2 和sin(x) 的系数return a*x**2 + b*np.sin(x)
然后我们可以使用scipy.optimize.curve_fit()来找到a和b:
guess = [2, 2] # 猜测的参数,合理设置该参数可以大幅度降低计算量
params, params_covariance = optimize.curve_fit(f2, xdata, ydata, guess)
params
array([ 0.99987461, 10.45777129])
plt.plot(xdata,ydata,linewidth=3)
a,b = params
plt.plot(xdata,f2(xdata,a,b))
[<matplotlib.lines.Line2D at 0x22ee2622a88>]
统计和随机数:scipy.stats
常见分布
可能用到的分布对照表
| 名称 | 含义 |
|---|---|
| beta | beta分布 |
| f | F分布 |
| gamma | gam分布 |
| poisson | 泊松分布 |
| hypergeom | 超几何分布 |
| lognorm | 对数正态分布 |
| binom | 二项分布 |
| uniform | 均匀分布 |
| chi2 | 卡方分布 |
| cauchy | 柯西分布 |
| laplace | 拉普拉斯分布 |
| rayleigh | 瑞利分布 |
| t | 学生T分布 |
| norm | 正态分布 |
| expon | 指数分布 |
通用函数
stats连续型随机变量的公共方法:
| 名称 | 备注 |
|---|---|
| rvs | 产生服从指定分布的随机数 |
| 概率密度函数 | |
| cdf | 累计分布函数 |
| sf | 残存函数(1-CDF) |
| ppf | 分位点函数(CDF的逆) |
| isf | 逆残存函数(sf的逆) |
| fit | 对一组随机取样进行拟合,最大似然估计方法找出最适合取样数据的概率密度函数系数。 |
- 离散分布的简单方法大多数与连续分布很类似,但是pdf被更换为密度函数pmf。
import numpy as np
from scipy import stats
a = np.random.normal(size=1000) # 生成正态分布
bins = np.arange(-4, 5) # -4~5的采样点
# a
bins
array([-4, -3, -2, -1, 0, 1, 2, 3, 4])
histogram = np.histogram(a, bins=bins, normed=True)[0]
bins = 0.5*(bins[1:] + bins[:-1])
bins
C:\Users\ASUS\Anaconda3\envs\tf2\lib\site-packages\ipykernel_launcher.py:1: VisibleDeprecationWarning: Passing `normed=True` on non-uniform bins has always been broken, and computes neither the probability density function nor the probability mass function. The result is only correct if the bins are uniform, when density=True will produce the same result anyway. The argument will be removed in a future version of numpy."""Entry point for launching an IPython kernel.array([-3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5])
from scipy import stats
import pylab as pl
b = stats.norm.pdf(bins) # 相当于np.random.normal,生成正态分布
pl.plot(bins, histogram)
pl.plot(bins, b)
pl.show()
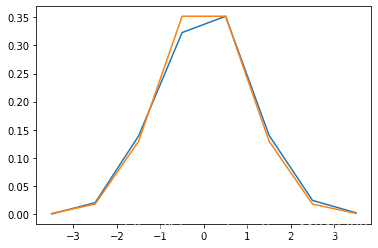
- 生成服从指定分布的随机数
norm.rvs通过loc和scale参数可以指定随机变量的偏移和缩放参数,这里对应的是正态分布的期望和标准差。size得到随机数数组的形状参数。(也可以使用np.random.normal(loc=0.0, scale=1.0, size=None))
normpdf = stats.norm.rvs(loc=0,scale=1.0,size=10)
normpdf
array([-0.35670277, -0.35593883, 0.55816991, -1.02267389, -0.26461898,1.46413836, -1.11843986, -1.67888616, 0.39230616, -0.32538297])
np.random.normal(loc=0.0, scale=1.0, size=10)
array([-0.17223573, 0.34488558, 1.30292964, -0.29186785, -0.35257427,-1.99991253, -0.27301159, 1.52191222, 0.51331207, 0.77448018])
stats.norm.rvs(loc = 3,scale = 10,size=(2,2))
array([[-8.97012362, 0.82079641],[ 6.5068092 , 8.60501163]])
- 求概率密度函数指定点的函数值
# stats.norm.pdf正态分布概率密度函数。
stats.norm.pdf(0,loc = 0,scale = 1) # 求原点的函数值
0.3989422804014327
stats.norm.pdf(np.arange(3),loc = 0,scale = 1)# 求0,1,2三个点的服从N~(0,1)标准正态分布的函数值
array([0.39894228, 0.24197072, 0.05399097])