章节
- SciPy 介绍
- SciPy 安装
- SciPy 基础功能
- SciPy 特殊函数
- SciPy k均值聚类
- SciPy 常量
- SciPy fftpack(傅里叶变换)
- SciPy 积分
- SciPy 插值
- SciPy 输入输出
- SciPy 线性代数
- SciPy 图像处理
- SciPy 优化
- SciPy 信号处理
- SciPy 统计
优化是指在某些约束条件下,求解目标函数最优解的过程。机器学习、人工智能中的绝大部分问题都会涉及到求解优化问题。
SciPy的optimize模块提供了许多常用的数值优化算法,一些经典的优化算法包括线性回归、函数极值和根的求解以及确定两函数交点的坐标等。
导入scipy.optimize模块,如下所示:
from scipy import optimize
标量函数极值求解
fmin_bfgs方法
函数f(x)是一个抛物线,求它的极小值:
f ( x ) = x 2 + 2 x + 9 f(x) = x^2 + 2x + 9 f(x)=x2+2x+9
我们先画出函数曲线:
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt# 定义函数
def f(x):return x**2 + 2*x + 9# x取值:-10到10之间,间隔0.1
x = np.arange(-10, 10, 0.1)# 画出函数曲线
plt.plot(x, f(x))
# plt.savefig('./opt2-1.png') # 保存要显示的图片
plt.show()
计算该函数最小值的有效方法之一是使用带起点的BFGS算法。该算法从参数给定的起始点计算函数的梯度下降,并输出梯度为零、二阶导数为正的极小值。BFGS算法是由Broyden,Fletcher,Goldfarb,Shanno四个人分别提出的,故称为BFGS校正。
示例
使用BFGS函数,找出抛物线函数的最小值:
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt# 定义函数
def f(x):return x**2 + 2*x + 9# x取值:-10到10之间,间隔0.1
x = np.arange(-10, 10, 0.1)# 画出函数曲线
plt.plot(x, f(x))# 第一个参数是函数名,第二个参数是梯度下降的起点。返回值是函数最小值的x值(ndarray数组)
xopt = optimize.fmin_bfgs(f, 0)xmin = xopt[0] # x值
ymin = f(xmin) # y值,即函数最小值
print('xmin: ', xmin)
print('ymin: ', ymin)# 画出最小值的点, s=20设置点的大小,c='r'设置点的颜色
plt.scatter(xmin, ymin, s=20, c='r')#plt.savefig('./opt3-1.png') # 保存要显示的图片
plt.show()输出
Optimization terminated successfully.Current function value: 8.000000Iterations: 2Function evaluations: 9Gradient evaluations: 3
xmin: -1.00000000944232
ymin: 8.0
fmin_bfgs有个问题,当函数有局部最小值,该算法会因起始点不同,找到这些局部最小而不是全局最小。
让我们看另一个函数,该函数有多个局部最小值:
g ( x ) = x 2 + 20 s i n ( x ) g(x) = x^2 + 20sin(x) g(x)=x2+20sin(x)
画出该函数的曲线:
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt# 定义函数
def g(x):return x**2 + 20*np.sin(x)# x取值:-10到10之间,间隔0.1
x = np.arange(-10, 10, 0.1)# 画出函数曲线
plt.plot(x, g(x))
# plt.savefig('./opt4-1.png') # 保存要显示的图片
plt.show()
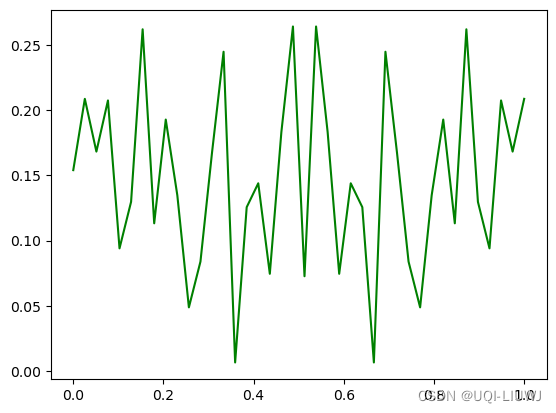
函数曲线
可以看到,该函数有多个底部。如果初始值设置不当,获得的最小值有可能只是局部最小值。
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt# 定义函数
def g(x):return x**2 + 20*np.sin(x)# x取值:-10到10之间,间隔0.1
x = np.arange(-10, 10, 0.1)# 画出函数曲线
plt.plot(x, g(x))# 第一个参数是函数名,第二个参数是梯度下降的起点。返回值是函数最小值的x值(ndarray数组)
# 可以看到5.0附近有个局部最小,把初始值设置为7, 返回的应该是这个局部最小值。
xopt = optimize.fmin_bfgs(g, 7)xmin = xopt[0] # x值
ymin = g(xmin) # y值,即函数最小值
print('xmin: ', xmin)
print('ymin: ', ymin)# 画出最小值的点, s=20设置点的大小,c='r'设置点的颜色
plt.scatter(xmin, ymin, s=20, c='r')#plt.savefig('./opt5-1.png') # 保存要显示的图片
plt.show()输出
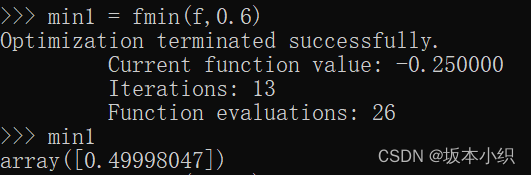
Optimization terminated successfully.Current function value: 0.158258Iterations: 3Function evaluations: 27Gradient evaluations: 9
xmin: 4.271095444673479
ymin: 0.15825752683190686可以看到5.0附近有个局部最小,把初始值设置为7, 返回的是这个局部最小值。
如果把初始值设置为0,应该就能返回真正的全局最小值:
basinhopping 方法
对于这种情况,可以使用scipy.optimize提供的basinhopping()方法。该方法把局部优化方法与起始点随机抽样相结合,求出全局最小值,代价是耗费更多计算资源。
调用语法
optimize.basinhopping(func, x0)
- func 目标函数
- x0 初始值
示例
import numpy as np
from scipy import optimize# 定义函数
def g(x):return x**2 + 20*np.sin(x)# 求取最小值,初始值为7
ret = optimize.basinhopping(g, 7)print(ret)输出
fun: 0.15825752683178962lowest_optimization_result: fun: 0.15825752683178962hess_inv: array([[0.04975718]])jac: array([4.76837158e-07])message: 'Optimization terminated successfully.'nfev: 12nit: 2njev: 4status: 0success: Truex: array([4.27109533])message: ['requested number of basinhopping iterations completed successfully']minimization_failures: 0nfev: 1641nit: 100njev: 547x: array([4.27109533])
可以看到全局最小值被正确找出:fun: 0.15825752683178962,x: array([4.27109533])
scipy.optimize.brute函数蛮力法也可用于全局优化,但效率较低。蛮力方法的语法为:
scipy.optimize.brute(f, 0)
fminbound
要求取一定范围之内的函数最小值,可使用fminbound方法。
调用语法
optimize.fminbound(func, x1, x2)
- func 目标函数
- x1, x2 范围边界
示例
import numpy as np
from scipy import optimize# 定义函数
def g(x):return x**2 + 20*np.sin(x)# 求取-10到-5之间的函数最小值。full_output=True表示返回详细信息。
ret = optimize.fminbound(g, -10, -5, full_output=True)print(ret)
输出
(-7.068891380019064, 35.82273589215206, 0, 12)
函数最小值是:35.82273589215206,对应的x值:-7.068891380019064。
函数求解
对于一个函数f(x),当f(x) = 0,求取x的值,即为函数求解。这种情况,可以使用fsolve()函数。
调用语法
optimize.fsolve(func, x0)
- func 目标函数
- x0 初始值
解单个方程
示例
解单个方程:
import numpy as np
from scipy import optimize# 定义函数
def g(x):return x**2 + 20*np.sin(x)# 函数求解
ret = optimize.fsolve(g, 2)print(ret)
输出
[0.]
解出的根值是:0
解方程组
如果要对如下方程组求解:
f 1 ( u 1 , u 2 , u 3 ) = 0 f 2 ( u 1 , u 2 , u 3 ) = 0 f 3 ( u 1 , u 2 , u 3 ) = 0 f1(u1,u2,u3) = 0 \\ f2(u1,u2,u3) = 0 \\ f3(u1,u2,u3) = 0 f1(u1,u2,u3)=0f2(u1,u2,u3)=0f3(u1,u2,u3)=0
func可以定义为:
def func(x):u1,u2,u3 = xreturn [f1(u1,u2,u3), f2(u1,u2,u3), f3(u1,u2,u3)]
示例
解方程组:
4 x + 9 = 0 3 y 2 − s i n ( y z ) = 0 y z − 2.5 = 0 4x + 9 = 0 \\ 3y^2 - sin(yz) = 0 \\ yz - 2.5 = 0 4x+9=03y2−sin(yz)=0yz−2.5=0
from scipy.optimize import fsolve
from math import sin,cosdef f(x):x0 = float(x[0])x1 = float(x[1])x2 = float(x[2])return [4*x1 + 9,3*x0*x0 - sin(x1*x2),x1*x2 - 2.5]
result = fsolve(f, [1,1,1])
print (result)
输出
[-0.44664383 -2.25 -1.11111111]
拟合
curve_fit
假设有一批数据样本,要创建这些样本数据的拟合曲线/函数,可以使用Scipy.optimize模块的curve_fit()函数。
调用形式
optimize.curve_fit(func, x1, y1)
- func 目标函数
- x1, y1 样本数据
我们将使用下面的函数来演示曲线拟合:
f ( x ) = 50 c o s ( x ) + 2 f(x) = 50cos(x) + 2 f(x)=50cos(x)+2
示例
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt# 函数模型用于生成数据
def g(x, a, b):return a*np.cos(x) + b# 产生含噪声的样本数据
x_data = np.linspace(-5, 5, 100) # 采样点
y_data = g(x_data, 50, 2) + 5*np.random.randn(x_data.size) # 加入随机数作为噪声# 使用curve_fit()函数来估计a和b的值
variables, variables_covariance = optimize.curve_fit(g, x_data, y_data)# 输出结果
print('\n求出的系数a, b: ')
print(variables)print('\nvariables_covariance: ')
print(variables_covariance)
输出
求出的系数a, b:
[49.66367999 2.09557981]variables_covariance:
[[0.55593391 0.10388677][0.10388677 0.26071478]]variables是给定模型的最优参数,variables_covariance可用于检查拟合情况,其对角线元素值表示每个参数的方差。可以看到我们正确求出了系数值。
绘制曲线:
import matplotlib.pyplot as plty = g(x_data, variables[0], variables[1])plt.plot(x_data, y_data, 'o', color="green", label = "Samples")
plt.plot(x_data, y, color="red", label = "Fit")
plt.legend(loc = "best")#plt.savefig('./opt10-1.png') # 保存要显示的图片
plt.show()生成
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-98kPUfcs-1571731570441)(https://www.qikegu.com/wp-content/uploads/2019/07/opt10-1.png)]
leastsq()函数
最小二乘法是非常经典的数值优化算法,通过最小化误差的平方和来寻找最符合数据的曲线。
optimize模块提供了实现最小二乘拟合算法的函数leastsq(),leastsq是least square的简写,即最小二乘法。
调用形式
optimize.leastsq(func, x0, args=())
- func 计算误差的函数
- x0 是计算的初始参数值
- args 是指定func的其他参数
示例
import numpy as np
from scipy import optimize # 样本数据
X = np.array([160,165,158,172,159,176,160,162,171]
Y = np.array([58,63,57,65,62,66,58,59,62])# 偏差函数, 计算以p为参数的直线和原始数据之间的误差
def residuals(p):k, b = preturn Y-(k*X+b)# leastsq()使得residuals()的输出数组的平方和最小,参数的初始值为[1, 0]
ret = optimize.leastsq(residuals, [1, 10])
k, b = ret[0]
print("k = ", k, "b = ", b)
输出
k = 0.4211697393502931 b = -8.288302606523974
绘制曲线:
import matplotlib.pyplot as plt#画样本点
plt.figure(figsize=(8, 6)) ##指定图像比例: 8:6
plt.scatter(X, Y, color="green", label="Samples", linewidth=2)#画拟合直线
x = np.linspace(150, 190, 100) ##在150-190直接画100个连续点
y = k*x + b ##函数式
plt.plot(x,y,color="red", label="Fit",linewidth=2)
plt.legend() #绘制图例
plt.savefig('./opt11-1.png') # 保存要显示的图片
plt.show()输出