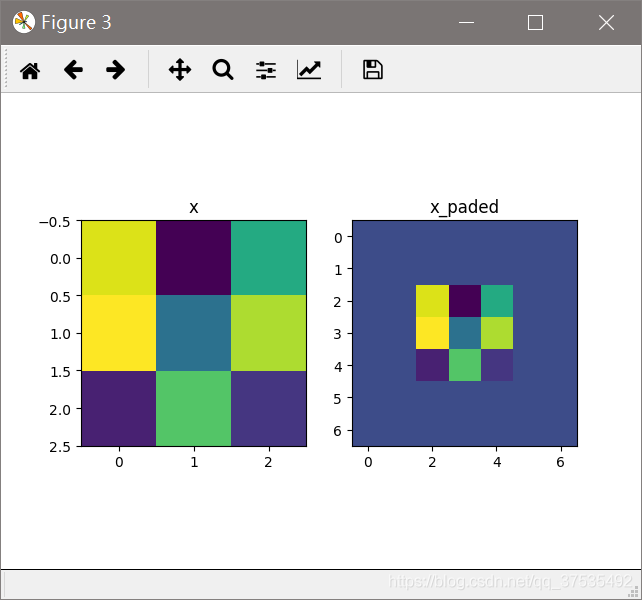
数学笔记;离散傅里叶变化 DFT_UQI-LIUWJ的博客-CSDN博客
数学笔记:FFT(快速傅里叶变换)_快速傅里叶变换矩阵_UQI-LIUWJ的博客-CSDN博客
【个人理解:FFT是DFT的一种优化,DFT需要N个谱域信号来表示N个时域信号,而FFT只需要N/2个谱域信号即可】
1 导入库&数据生成
import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as pltx=np.linspace(0,1,40)
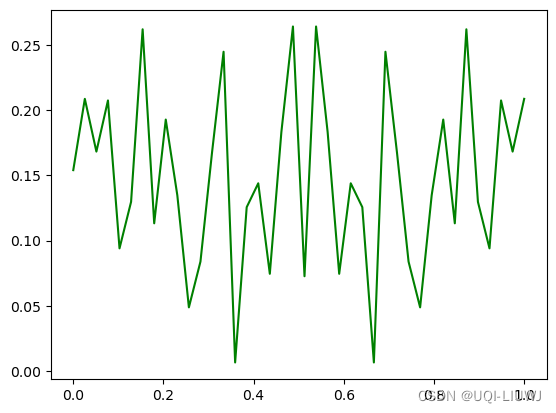
y=np.random.randn(40)plt.plot(x,y)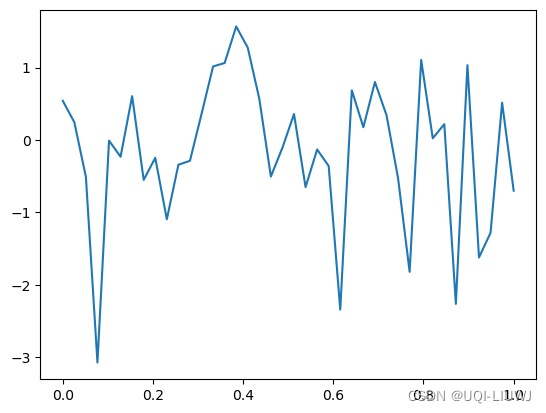
2 FFT
fft_y=fft(y)
len(fft_y)
#40fft_y
'''
array([-6.15873059-0.j , -7.29200331-4.05456983j,-2.23578346+6.34453713j, 6.56731493-5.0657468j ,-2.65104048+2.66979677j, 3.35337807+3.95677639j,10.36303604+1.52428879j, 0.51714401+4.49958009j,2.48422329-7.29706994j, 4.356219 -3.17138859j,1.8923956 +0.48467422j, -3.28973165-0.661626j ,-6.69114433-0.14581842j, -4.57713041-8.65049585j,0.13366315-0.22953073j, -3.70512463-3.39291042j,
...
'''abs_y=np.abs(fft_y)
plt.plot(x,abs_y)
经过FFT之后,得到的是40个谱域的点,且关于0.5轴对称
——>40个谱域的点相当于DFT的结果,FFT的话只需要取前一半即可
2.1 振幅归一化
上面是振幅未归一化的情况,如果对振幅进行归一化,则有:
normalization_y=abs_y/40
plt.plot(x,normalization_y,'g')