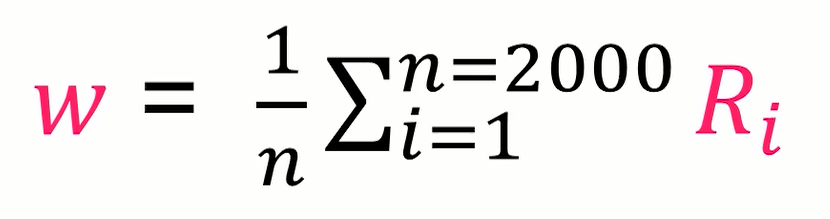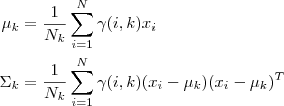高斯混合模型学习笔记
根据师兄(王延凯的博客)以及其他博主大佬的总结学习高斯混合模型,自己也作一下学习记录。
目录
- 高斯混合模型学习笔记
- 1、模型介绍
- 2、模型求解步骤
- 举个栗子
- 通用背景模型UBM[\[2\]](https://blog.csdn.net/weixin_44278406/article/details/103853779)
- 参考:
1、模型介绍
高斯混合模型(Gaussian Mixture Mode), K K K个高斯分布 g ( x ∣ μ k , ∑ k ) g\left( x|\mu _k,\sum_k{} \right) g(x∣μk,∑k)(均值为 μ k \mu_k μk协方差矩阵为 ∑ k \sum_k ∑k)以权重为 ω k \omega_k ωk线性组合( ∑ k K ω k = 1 \sum_k^K{\omega_k}=1 ∑kKωk=1)的概率分布模型[1]。
P ( x ) = ∑ k = 1 K ω k g ( x ∣ μ k , ∑ k ) P(x)=\sum_{k=1}^{K}{\omega_kg(x|\mu_k,\sum _k)} P(x)=k=1∑Kωkg(x∣μk,k∑)
多个一维高斯分布叠加为一个一维高斯分布,当 K = 2 K=2 K=2时,对于一维高斯分布不同权重 ω k \omega_k ωk叠加而成的一维高斯分布如下:

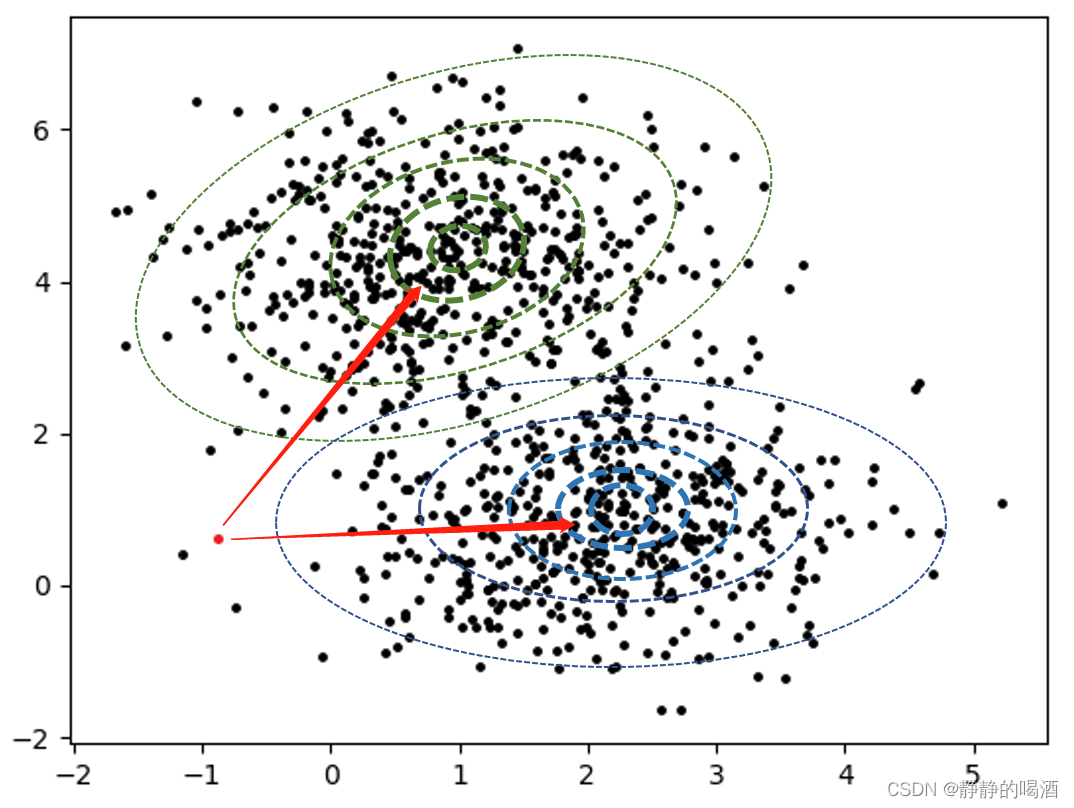
同样的二维高斯分布叠加:
K = 2 K=2 K=2时,平面点阵及三维视图如下:


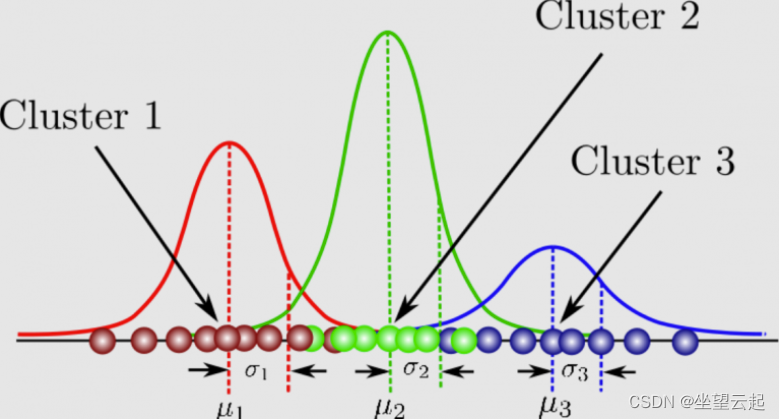
K = 3 K=3 K=3时,三维视图如下:

到此,我们可以看出高斯混合模型的3个基本参数,均值 μ k \mu_k μk,方差 σ k 2 \sigma_k^2 σk2(替代协方差),权重 ω k \omega_k ωk。
2、模型求解步骤
步骤中包含期望最大化(EM)算法:
Step 1. 初始化参数:初始化高斯混合模型的3个基本参数,均值 μ k \mu_k μk,方差 σ k 2 \sigma_k^2 σk2(替代协方差),权重 ω k \omega_k ωk。
计算每个高斯分布中(假设每个分布数据量相同)所有混合数据 x j x_j xj( j = 1 , 2 , , ⋯ , K ∗ N j=1,2,,\cdots,K*N j=1,2,,⋯,K∗N)在第 k k k个高斯分布 g ( x ∣ μ k , ∑ k ) g\left( x|\mu _k,\sum_k{} \right) g(x∣μk,∑k)的响应值 R i ( k ) R_i^{(k)} Ri(k),其中 i = 1 , 2 , ⋯ , N i=1,2,\cdots,N i=1,2,⋯,N,表示每个分布有N个元素:
g ( x i ∣ μ k , σ k ) = 1 2 π σ k e − ( x i − u k ) 2 2 σ k 2 g(x_i|\mu_k,\sigma_k)=\frac{1}{\sqrt{2\pi}\sigma_k}e^{-\frac{{(x_i-u_k)}^2}{2\sigma_k^2}} g(xi∣μk,σk)=2πσk1e−2σk2(xi−uk)2
R j ( k ) = ω k ∗ g ( x j ∣ μ k , σ k ) ∑ k = 1 K ω k ∗ g ( x j ∣ μ k , σ k ) R_j^{(k)}=\frac{\omega_k*g(x_j|\mu_k,\sigma_k)}{\sum_{k=1}^K{\omega_k*g(x_j|\mu_k,\sigma_k)}} Rj(k)=∑k=1Kωk∗g(xj∣μk,σk)ωk∗g(xj∣μk,σk)
此时得到所有(混合)数据 x i x_i xi关于不同分布 g ( x i ∣ μ k , σ k ) g(x_i|\mu_k,\sigma_k) g(xi∣μk,σk)的响应值 R i ( k ) R_i^{(k)} Ri(k)( x j x_j xj落入第k个高斯分量下的后验概率)。
Step 2.更新第K个分布的期望 μ k \mu_k μk:
μ k ( n e w ) = ∑ j = 1 K ∗ N R j ( k ) ∗ x j ∑ j = 1 K ∗ N R j ( k ) \mu_k^{(new)}=\frac{ \sum_ {j=1}^{K*N}{R_j^{(k)}*x_j}}{ \sum_ {j=1}^{K*N}{R_j^{(k)}} } μk(new)=∑j=1K∗NRj(k)∑j=1K∗NRj(k)∗xj
Step 3.更新第K个分布的,方差 σ k 2 \sigma_k^2 σk2:
σ k 2 ( n e w ) = ∑ j = 1 K ∗ N R j ( k ) ∗ ( x j − μ k ) 2 ∑ j = 1 K ∗ N R j ( k ) \sigma_k^{2(new)}=\frac{ \sum_ {j=1}^{K*N}{R_j^{(k)}*{(x_j-\mu_k)^2 }}}{ \sum_ {j=1}^{K*N}{R_j^{(k)}} } σk2(new)=∑j=1K∗NRj(k)∑j=1K∗NRj(k)∗(xj−μk)2
Step 3.更新权值 ω k \omega_k ωk:
ω k = 1 K ∗ N ∑ j = 1 K ∗ N R j ( k ) \omega_k=\frac{1}{K*N}\sum_ {j=1}^{K*N}{R_j}^{(k)} ωk=K∗N1j=1∑K∗NRj(k)
参数多次更新后趋于稳定,即收敛。
举个栗子
最后列出[1]中三个高斯分布的参数更新
不同类别权重随迭代次数的变化:

迭代15次后得知的三个高斯正态分布的概率密度曲线。

高斯混合模型的随迭代次数的变化而变化图形:

代码参考:[1]
求解高斯混合模型就是输入数据迭代更新均值 μ k \mu_k μk,方差 σ k 2 \sigma_k^2 σk2,权重 ω k \omega_k ωk并且使之更新后趋于稳定的的过程,迭代更新参数的方法为极大四估计法。
通用背景模型UBM[2]
(1)通用背景模型采用背景数据(大量的不限分布列,允许包含在K集之内的数据,数据来自训练分布列)训练高斯混合模型。
(2)采用少量的某个分布列数据通过MAP(极大后验推测)算法调整UBM模型参数进行自适应,拟合得到某个K集合分布列构成的高斯混合模型GMM参数。

step1:计算某个 x i x_i xi在第k个分布的的后验概率 R j ( k ) R_j^{(k)} Rj(k)
step2:更新均值
MAP算法描述如下图:

目前语音识别/说话人识别等技术中使用的自适应方法主要分为两大类:
基于最大后验概率(Maximum a posteriori, MAP)的算法
基本准则是后验概率最大化,利用贝叶斯学习( Bayesian learning)理论,将UBM系统的先验信息与被适应人(目标说话人)的信息相结合实现自适应;
基于变换(如MLLR)的方法
估计UBM系统模型与被适应人之间的变换关系,对UBM系统的模型或输入语音特征作变换,减少UBM系统与被适应人之间的差异。
参考:
[1]高斯混合模型GMM—【1】
[2]声纹识别-2.GMM-UBM(高斯混合模型-通用背景模型)