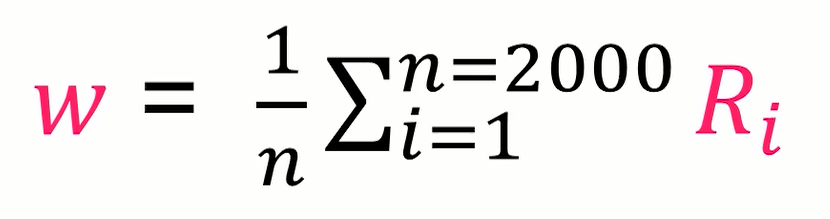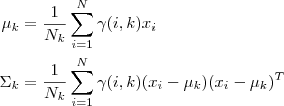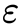高斯混合模型
- 前言
- 高斯混合模型
- 高斯分布
- 混合模型
- 高斯模型
- 单高斯模型
- 高斯混合模型
- 高斯混合模型训练
- EM算法
- 应用
- 图像背景的高斯混合模型
- 智能监控系统
- 参考
前言
之前在一次技术讨论当中,针对文本处理的时候被问到高斯混合模型。当时我对“高斯混合模型”都是比较懵圈,因此写下这篇笔记来记录高斯混合模型。高斯混合模型比较经典,有很多相关的资料也做了非常详细的介绍,本博客的参考内容请见参考部分
高斯混合模型
高斯混合模型通常简称GMM,是一种业界广泛使用的聚类算法,该方法使用了高斯分布作为参数模型,并使用期望最大(Expectation Maximization,简称EM)算法进行训练。
高斯分布
高斯分布有时也被成为正态分布,是一种自然界大量存在的,最为常见的分布形式。高斯分布的概率密度函数公式如下: f ( x ∣ μ , σ 2 ) = 1 2 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\sigma^2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x∣μ,σ2)=2σ2π1e−2σ2(x−μ)2其中 μ \mu μ表示均值, σ \sigma σ表示标准差,均值对应正态分布的中间位置。正态分布意思是95%的数据分布在均值周围2个标准差的范围内。上面公式在一直参数的情况下,输入变量 x x x,可以获得对应的概率密度。在使用之前需要对概率分布进行归一化,即曲线下面的面积之和为1,这样才能确保返回的概率密度在允许的取值范围内。
混合模型
混合模型是一个可以用来表示在总体分布中含有K个子分布的概率模型。换言之概率模型表示了观测数据在总体中的概率分布,它是由K个子分部组成的混合分布。混合模型不要求观测数据提供关于子分部的信息,来计算观测数据在总体分布中的概率。
高斯模型
单高斯模型
当样本数据 X X X是一维数据时,高斯分布遵从下方的概率密度函数: f ( x ∣ μ , σ 2 ) = 1 2 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\sigma^2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x∣μ,σ2)=2σ2π1e−2σ2(x−μ)2其中 μ \mu μ表示均值, σ \sigma σ表示标准差。当样本数据数据是多维数据的时,高斯分布遵从下方概率密度函数: P ( x ∣ θ ) = 1 ( 2 π ) D 2 ∣ ∑ ∣ 1 2 e x p ( − ( x − μ ) T ∑ − 1 ( x − μ ) 2 ) P(x|\theta) = \frac{1}{(2\pi)^{\frac{D}{2}}|\sum|^\frac{1}{2}}exp(-\frac{(x-\mu)^T\sum^{-1}(x-\mu)}{2}) P(x∣θ)=(2π)2D∣∑∣211exp(−2(x−μ)T∑−1(x−μ))其中, μ \mu μ为数据均值(期望), ∑ \sum ∑为协方差, D D D为数据维度。
高斯混合模型
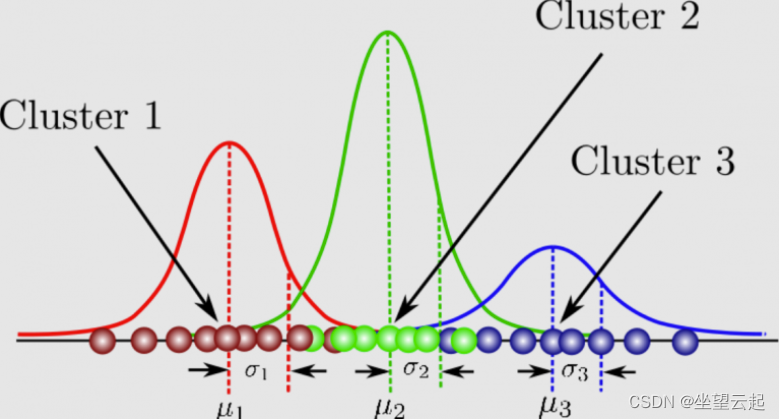
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量(Hidden variable)。一般来说,一个混合模型可以使用任何概率分布,这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。

首先定义一下信息:
- x j x_j xj表示第 j j j个观测数据, j = 1 , 2 , ⋯ , N j=1,2,\cdots,N j=1,2,⋯,N
- K K K是很合模型中高斯模型的数量, k = 1 , 2 , ⋯ , K k=1,2,\cdots,K k=1,2,⋯,K
- a k a_k ak是观测数据属于第 k k k个子模型的高斯分布密度函数, a k ≥ 0 , ∑ k = 1 K a k = 1 a_k\geq0,\sum^K_{k=1}a_k=1 ak≥0,∑k=1Kak=1
- ϕ ( x ∣ θ k ) \phi(x|\theta_k) ϕ(x∣θk)是第 k k k个子模型的高斯分布密度函数, θ k = ( μ k , σ k 2 ) \theta_k=(\mu_k, \sigma^2_k) θk=(μk,σk2)
- γ j k \gamma_{jk} γjk表示第 j j j个观测数据属于第 k k k个子模型的概率
高斯混合模型的概率分布为: P ( x ∣ θ ) = ∑ k = 1 K a k ϕ ( x ∣ θ k ) P(x|\theta) = \sum^K_{k=1}a_k\phi(x|\theta_k) P(x∣θ)=k=1∑Kakϕ(x∣θk)对于模型而言,参数 θ = ( μ k ^ , σ k ^ , a k ^ ) \theta=(\hat{\mu_k}, \hat{\sigma_k}, \hat{a_k}) θ=(μk^,σk^,ak^),每个子模型的期望、方差(协方差)、在混合模型中发生的概率。
高斯混合模型训练
模型的EM训练过程,通过观察采样的概率值和模型概率值的接近程度来判断一个模型是否拟合良好。然后通过调整模型以让新模型更适配采样的概率值。反复迭代这个过程很多次,直到两个概率值非常接近时停止更新并完成模型训练。
-
单高斯模型
使用极大似然法估算参数 θ \theta θ, θ = a r g m a x θ L ( θ ) \theta = argmax_\theta L(\theta) θ=argmaxθL(θ)这里假设每个数据点都是独立的,似然函数由概率密度函数给出 L ( θ ) = ∏ j = 1 N P ( x j ∣ θ ) L(\theta)=\prod^N_{j=1}P(x_j|\theta) L(θ)=j=1∏NP(xj∣θ)由于每个点发生的概率都很小,乘积会变得很小,因此通常利用maximum Log-Likelihood: log L ( θ ) = ∑ j = 1 N log P ( x j ∣ θ ) \log L(\theta)= \sum^N_{j=1}\log P(x_j|\theta) logL(θ)=j=1∑NlogP(xj∣θ) -
高斯混合模型
Log-Likelihood函数是: log L ( θ ) = ∑ j = 1 N log P ( x j ∣ θ ) = ∑ j = 1 N log ( ∑ k = 1 K a k ϕ ( x ∣ θ k ) ) \log L(\theta)= \sum^N_{j=1}\log P(x_j|\theta) = \sum^N_{j=1}\log(\sum^K_{k=1}a_k\phi(x|\theta_k)) logL(θ)=j=1∑NlogP(xj∣θ)=j=1∑Nlog(k=1∑Kakϕ(x∣θk))形如这种每个子模型都有未知的 a k , μ k , σ k a_k,\mu_k,\sigma_k ak,μk,σk需要通过迭代的方法求解高斯混合模型的参数。
EM算法

应用
图像背景的高斯混合模型
图像灰度直方图反映的是图像中某个灰度值出现的频次,也可以以为是图像灰度概率密度的估计。如果图像所包含的目标区域和背景区域相差比较大,且背景区域和目标区域在灰度上有一定的差异,那么该图像的灰度直方图呈现双峰-谷形状,其中一个峰对应于目标,另一个峰对应于背景的中心灰度。对于复杂的图像,尤其是医学图像,一般是多峰的。通过将直方图的多峰特性看作是多个高斯分布的叠加,可以解决图像的分割问题。
智能监控系统
在智能监控系统中,对于运动目标的检测是中心内容,而在运动目标检测提取中,背景目标对于目标的识别和跟踪至关重要。而建模正是背景目标提取的一个重要环节。
参考
- 一文详解高斯混合模型原理
- 斯混合模型(GMM)