2020/10/31:初稿，参考https://walkccc.github.io/CLRS/Chap04/4.1/，并增加相应的Python代码.

4 Divide-and-Conquer

4.1 The maximum-subarray problem

1.What does FIND-MAXIMUM-SUBARRAY return when all elements of A are negative?
It will return a single-element array with the largest negative integer.

2.Write pseudocode for the brute-force method of solving the maximum-subarray problem. Your procedure should run in $O(n^2)$ time.

FIND-MAX-SUBARRAY(A, low, high)left = 0right = 0sum = -∞for i = low to highcurrent-sum = 0for j = i to highcurrent-sum += A[j]if sum < current-sumsum = current-sumleft = iright = jreturn (left, right, sum)

Python Implementation:

def find_max_crossing_subarray(A,low,mid,high):# Defining a negative infinite integerleft_sum = float("-inf")sum = 0for i in range(mid,low -1 ,-1):sum += A[i]if sum > left_sum:left_sum = summax_left = iright_sum = float("-inf")sum = 0for j in range(mid+1, high + 1):sum += A[j]if sum > right_sum:right_sum = summax_right = jreturn (max_left, max_right, left_sum + right_sum)def find_max_subarray(A,low,high):if high == low:return (low,high,A[low])else:mid = (low + high) // 2left_low, left_high, left_sum = find_max_subarray(A, low, mid)right_low, right_high, right_sum = find_max_subarray(A, mid + 1, high)cross_low, cross_high, cross_sum = find_max_crossing_subarray(A, low, mid, high)if left_sum >= right_sum and left_sum >=cross_sum:return (left_low,left_high,left_sum)elif right_sum >= left_sum and right_sum >=cross_sum:return (right_low,right_high,right_sum)else:return (cross_low,cross_high,cross_sum)nums=[13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]
print(find_max_subarray(nums,0,len(nums)-1))nums=[-2,1,-3,4,-1,2,1,-5,4]
print(find_max_subarray(nums,0,len(nums)-1))

3.Implement both the brute-force and recursive algorithms for the maximum-subarray problem on your own computer. What problem size $n_0$ gives the crossover point at which the recursive algorithm beats the brute-force algorithm? Then, change the base case of the recursive algorithm to use the brute-force algorithm whenever the problem size is less than $n_0$ . Does that change the crossover point?

I think the value $n_0$ varies on different computers and different arrays. To me $n_0=47$ . Python implemention for the comparision:

import timedef find_max_subarray_bf(A,low,high):left = 0right = 0sum = float("-inf")for i in range(0, high + 1):current_sum = 0for j in range(i, high + 1):#get sum of nums[i..j]current_sum += A[j]if sum < current_sum:sum = current_sumleft = iright = jreturn (left,right,sum)def find_max_crossing_subarray(A,low,mid,high):# Defining a negative infinite integerleft_sum = float("-inf")sum = 0for i in range(mid,low -1 ,-1):sum += A[i]if sum > left_sum:left_sum = summax_left = iright_sum = float("-inf")sum = 0for j in range(mid+1, high + 1):sum +=A[j]if sum > right_sum:right_sum = summax_right = jreturn (max_left, max_right, left_sum + right_sum)def find_max_subarray_rc(A,low,high):if high == low:return (low,high,A[low])else:mid = (low + high) // 2left_low, left_high, left_sum = find_max_subarray_rc(A, low, mid)right_low, right_high, right_sum = find_max_subarray_rc(A, mid + 1, high)cross_low, cross_high, cross_sum = find_max_crossing_subarray(A, low, mid, high)if left_sum >= right_sum and left_sum >=cross_sum:return (left_low,left_high,left_sum)elif right_sum >= left_sum and right_sum >=cross_sum:return (right_low,right_high,right_sum)else:return (cross_low,cross_high,cross_sum)A = [20, -21, 43, -23, -92, 45, -56, -5, 34, -17,34, 65, 89, -109, 125, 2, -10, 89, 46, 65, -49, 3, -45, 34, 76, 32, -76, -2, 3, -45, 44, 34, 67, -67, 99, -104, 11, -37, 44, 76, -90, 89, -32, 34, 88, 56, -6, -89, -90, -34, -56, 23, 29, 2, 6, 9, 2, -34, -45, 34, 22, -177, 44, 90, -45, -36, 55, 23, 56, -56, -167, -54, 23, 45, 14, 62, -46, -56, -34, 45, 32, 20, -87, 39, 82, 95, -67, -45, 88, -36, 21, 18, 16, 81, -102, 99, -45, -67, -45, -76]for n in range(1, len(A)):start = time.process_time()for i in range(0, 10000):find_max_subarray_bf(A, 0, n-1)stop = time.process_time()duration_bf = stop - startstart = time.process_time()for i in range(0, 10000):find_max_subarray_rc(A, 0, n-1)stop = time.process_time()duration_rc = stop - startprint('n={},duration of bf and rc:{} and {}'.format(n,duration_bf,duration_rc))if duration_bf > duration_rc:print('recursive beats brute-force when n={}'.format(n))def find_max_subarray_mixed(A,low,high):if high - low < 47:return find_max_subarray_bf(A, low, high)else:mid = (low + high ) //2left_low,left_high,left_sum = find_max_subarray_mixed(A, low, mid)right_low,right_high,right_sum = find_max_subarray_mixed(A, mid, high)cross_low,cross_high,cross_sum = find_max_crossing_subarray(A, low, mid, high)if left_sum >= right_sum and left_sum >=cross_sum:return (left_low,left_high,left_sum)elif right_sum >= left_sum and right_sum >=cross_sum:return (right_low,right_high,right_sum)else:return (cross_low,cross_high,cross_sum)A = [20, -21, 43, -23, -92, 45, -56, -5, 34, -17,34, 65, 89, -109, 125, 2, -10, 89, 46, 65, -49, 3, -45, 34, 76, 32, -76, -2, 3, -45, 44, 34, 67, -67, 99, -104, 11, -37, 44, 76, -90, 89, -32, 34, 88, 56, -6, -89, -90, -34, -56, 23, 29, 2, 6, 9, 2, -34, -45, 34, 22, -177, 44, 90, -45, -36, 55, 23, 56, -56, -167, -54, 23, 45, 14, 62, -46, -56, -34, 45, 32, 20, -87, 39, 82, 95, -67, -45, 88, -36, 21, 18, 16, 81, -102, 99, -45, -67, -45, -76]for n in range(1, len(A)):start = time.process_time()for i in range(0, 10000):bf_result = find_max_subarray_bf(A, 0, n-1)stop = time.process_time()duration_bf = stop - startstart = time.process_time()for i in range(0, 10000):mix_result = find_max_subarray_mixed(A, 0, n-1)stop = time.process_time()duration_mix = stop - startprint('n={},duration of bf and mixed:{} and {}'.format(n,duration_bf,duration_mix))print('bf result:{},mixed result:{}'.format(bf_result, mix_result))if duration_bf > duration_mix:print('mixed beats brute-force when n={}'.format(n))

If the algorithm is modified to used divide and conquer when n≥47 and the brute-force approach when n is less, the performance at the crossover point almost doubles. The performance at $n_0 - 1$ stays the same, though (or even gets worse, because of the added overhead).

What I find interesting is that if we set $n_0 - 1$ and used the mixed approach to sort 40 elements, it is still faster than both.

4.Suppose we change the definition of the maximum-subarray problem to allow the result to be an empty subarray, where the sum of the values of an empty subarray is 00. How would you change any of the algorithms that do not allow empty subarrays to permit an empty subarray to be the result?

If the original algorithm returns a negative sum, returning an empty subarray instead.

5.Use the following ideas to develop a nonrecursive, linear-time algorithm for the maximum-subarray problem. Start at the left end of the array, and progress toward the right, keeping track of the maximum subarray seen so far. Knowing a maximum subarray A[1..j], extend the answer to find a maximum subarray ending at index j + 1 by using the following observation: a maximum subarray A[i..j + 1], for some 1≤i≤j+1. Determine a maximum subarray of the form A[i..j+1] in constant time based on knowing a maximum subarray ending at index j.

ITERATIVE-FIND-MAXIMUM-SUBARRAY(A)n = A.lengthmax-sum = -∞sum = -∞for j = 1 to ncurrentHigh = jif sum > 0sum = sum + A[j]elsecurrentLow = jsum = A[j]if sum > max-summax-sum = sumlow = currentLowhigh = currentHighreturn (low, high, max-sum)

Python Implementation:

def find_max_subarray_dp(A):n = len(A)max_sum = float("-inf")current_sum = float("-inf")low = float("-inf")high = float("-inf")for j in range(0, n):current_high = jif current_sum > 0:current_sum = current_sum + A[j]else:current_sum = A[j]current_low = jif current_sum > max_sum:max_sum = current_sumlow = current_lowhigh = current_highreturn (low,high,max_sum)nums=[13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]
print(find_max_subarray_dp(nums))nums=[-2,1,-3,4,-1,2,1,-5,4]
print(find_max_subarray_dp(nums))

4.2 Strassen's algorithm for matrix multiplication

1.Use Strassen's algorithm to compute the matrix product

$\begin{pmatrix} 1 & 3 \\ 7 & 5 \end{pmatrix} \begin{pmatrix} 6 & 8 \\ 4 & 2 \end{pmatrix}$

Show your work.

The first matrices are

$\begin{array}{ll} S_1 = 6 & S_6 = 8 \\ S_2 = 4 & S_7 = -2 \\ S_3 = 12 & S_8 = 6 \\ S_4 = -2 & S_9 = -6 \\ S_5 = 6 & S_{10} = 14. \end{array}$

The result is

$\begin{pmatrix} 18 & 14 \\ 62 & 66 \end{pmatrix}$ .

2.Write pseudocode for Strassen's algorithm.

STRASSEN(A, B)n = A.rowsif n == 1return a[1, 1] * b[1, 1]let C be a new n × n matrixA[1, 1] = A[1..n / 2][1..n / 2]A[1, 2] = A[1..n / 2][n / 2 + 1..n]A[2, 1] = A[n / 2 + 1..n][1..n / 2]A[2, 2] = A[n / 2 + 1..n][n / 2 + 1..n]B[1, 1] = B[1..n / 2][1..n / 2]B[1, 2] = B[1..n / 2][n / 2 + 1..n]B[2, 1] = B[n / 2 + 1..n][1..n / 2]B[2, 2] = B[n / 2 + 1..n][n / 2 + 1..n]S[1] = B[1, 2] - B[2, 2]S[2] = A[1, 1] + A[1, 2]S[3] = A[2, 1] + A[2, 2]S[4] = B[2, 1] - B[1, 1]S[5] = A[1, 1] + A[2, 2]S[6] = B[1, 1] + B[2, 2]S[7] = A[1, 2] - A[2, 2]S[8] = B[2, 1] + B[2, 2]S[9] = A[1, 1] - A[2, 1]S[10] = B[1, 1] + B[1, 2]P[1] = STRASSEN(A[1, 1], S[1])P[2] = STRASSEN(S[2], B[2, 2])P[3] = STRASSEN(S[3], B[1, 1])P[4] = STRASSEN(A[2, 2], S[4])P[5] = STRASSEN(S[5], S[6])P[6] = STRASSEN(S[7], S[8])P[7] = STRASSEN(S[9], S[10])C[1..n / 2][1..n / 2] = P[5] + P[4] - P[2] + P[6]C[1..n / 2][n / 2 + 1..n] = P[1] + P[2]C[n / 2 + 1..n][1..n / 2] = P[3] + P[4]C[n / 2 + 1..n][n / 2 + 1..n] = P[5] + P[1] - P[3] - P[7]return C

3.How would you modify Strassen's algorithm to multiply n×n matrices in which nn is not an exact power of 2? Show that the resulting algorithm runs in time Θ(nlg7).

We can just extend it to n×n matrix and pad it with zeroes. It's obviously Θ(nlg7).

4.What is the largest k such that if you can multiply 3×3 matrices using k multiplications (not assuming commutativity of multiplication), then you can multiply n×n matrices is time o(nlg7)? What would the running time of this algorithm be?

Assume $n = 3^m$ for some m. Then, using block matrix multiplication, we obtain the recursive running time T(n) = kT(n / 3) + O(1).

By master theorem, we can find the largest k to satisfy $\log_3 k < \lg 7$ is k=21.

5.V. Pan has discovered a way of multiplying $68 \times 68$ matrices using 132464 multiplications, a way of multiplying 70×70 matrices using 143640 multiplications, and a way of multiplying 72×72 matrices using 155424 multiplications. Which method yields the best asymptotic running time when used in a divide-and-conquer matrix-multiplication algorithm? How does it compare to Strassen's algorithm?

Using what we know from the last exercise, we need to pick the smallest of the following

$\begin{aligned} \log_{68} 132464 & \approx 2.795128 \\ \log_{70} 143640 & \approx 2.795122 \\ \log_{72} 155424 & \approx 2.795147. \end{aligned}$

The fastest one asymptotically is 70×70 using 143640.

6.How quickly can you multiply a kn×n matrix by an n×kn matrix, using Strassen's algorithm as a subroutine? Answer the same question with the order of the input matrices reversed.

(kn×n)(n×kn) produces a kn×kn matrix. This produces $k^2$ multiplications of n×n matrices.
(n×kn)(kn×n) produces an n×n matrix. This produces k multiplications and k−1 additions.

7.Show how to multiply the complex numbers $a+bi$ and $c+di$ using only three multiplications of real numbers. The algorithm should take a, b, c and d as input and produce the real component ac−bd and the imaginary component ad+bc separately.

4.3 The substitution method for solving recurrences

1.Show that the solution of T(n) = T(n - 1) + n is $O(n^2)$ .

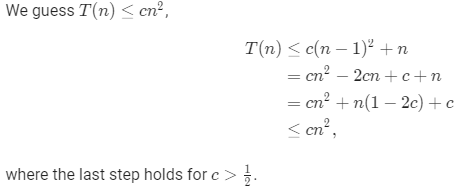
2.Show that the solution of T(n)=T(⌈n/2⌉)+1 is O(lgn).

3.We saw that the solution of T(n)=2T(⌊n/2⌋)+n is O(nlgn). Show that the solution of this recurrence is also Ω(nlgn). Conclude that the solution is Θ(nlgn).

4.Show that by making a different inductive hyptohesis, we can overcome the difficulty with the boundary condition T(1)=1 for recurrence (4.19) without adjusting the boundary conditions for the inductive proof.

5.Show that Θ(nlgn) is the solution to the "exact" recurrence (4.3) for merge sort.

The recurrence is

$T(n) = T(\lceil n / 2 \rceil) + T(\lfloor n / 2 \rfloor) + \Theta(n)$

To show Θ bound, separately show O and Ω bounds.

6.Show that the solution toT(n)=2T(⌊n/2⌋+17)+n is O(nlgn).

7.Using the master method in Section 4.5, you can show that the solution to the recurrence T(n)=4T(n/3)+n is $T(n)=\Theta(n\log_{3}{ 4})$ . Show that a substitution proof with the assumption $T(n) \le cn^{\log_3 4}$ fails. Then show how to subtract off a lower-order term to make the substitution proof work.

8.Using the master method in Section 4.5, you can show that the solution to the recurrence $T(n)=4T(n/2)+n^2$ is $T(n) = \Theta(n^2)$ . Show that a substitution proof with the assumption $T(n) \le cn^2$ fails. Then show how to subtract off a lower-order term to make the substitution proof work.

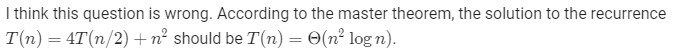
9.Solve the recurrence $T(n) = 3T(\sqrt n) + \log n$ by making a change of variables. Your solution should be asymptotically tight. Do not worry about whether values are integral.

4.4 The recursion-tree method for solving recurrences

1.Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n)=3T(⌊n/2⌋)+n. Use the substitution method to verify your answer.

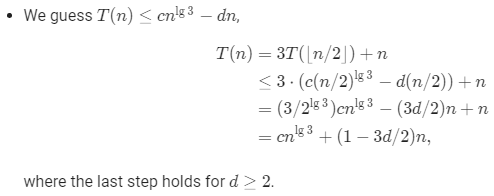
2.Use a recursion tree to determine a good asymptotic upper bound on the recurrence $T(n) = T(n / 2) + n^2$ . Use the substitution method to verify your answer.

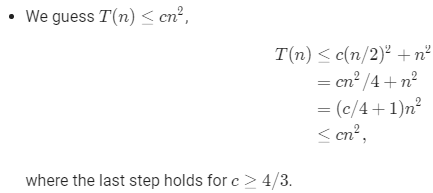
3.Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n)=4T(n/2+2)+n. Use the substitution method to verify your answer.

4.Use a recursion tree to determine a good asymptotic upper bound on the recurrenceT(n)=2T(n−1)+1. Use the substitution method to verify your answer.

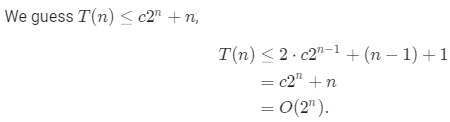
5.Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n)=T(n−1)+T(n/2)+n. Use the substitution method to verify your answer.

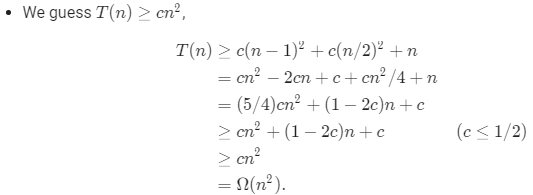
6.Argue that the solution to the recurrence T(n) = T(n / 3) + T(2n / 3) + cn, where c is a constant, is Ω(nlgn) by appealing to the recursion tree.

We know that the cost at each level of the tree is cncn by examining the tree in figure 4.6. To find a lower bound on the cost of the algorithm, we need a lower bound on the height of the tree.

The shortest simple path from root to leaf is found by following the leftest child at each node. Since we divide by 33 at each step, we see that this path has length $\log_3 n$ . Therefore, the cost of the algorithm is

$cn(\log_3 n + 1) \ge cn\log_3 n = \frac{c}{\log_3} n\log n = \Omega(n\log n).$

7.Draw the recursion tree for T(n)=4T(⌊n/2⌋)+cn, where c is a constant, and provide a tight asymptotic bound on its solution. Verify your answer with the substitution method.

8.Use a recursion tree to give an asymptotically tight solution to the recurrence T(n)=T(n−a)+T(a)+cn, wherea≥1 and c>0 are constants.

9.Use a recursion tree to give an asymptotically tight solution to the recurrence T(n)=T(αn)+T((1−α)n)+cn, where α is a constant in the range 0<α<1, and c>0 is also a constant.

4.5 The master method for solving recurrences

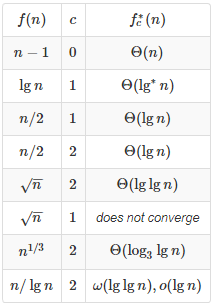
1.Use the master method to give tight asymptotic bounds for the following recurrences:

a. T(n) = 2T(n / 4) + 1

b. $T(n) = 2T(n / 4) + \sqrt n$

c. T(n) = 2T(n / 4) + n

d. $T(n) = 2T(n / 4) + n^2$

a. $\Theta(n^{\log_4 2}) = \Theta(\sqrt n)$

b. $\Theta(n^{\log_4 2}\lg n) = \Theta(\sqrt n\lg n)$

c. $\Theta(n)Θ(n)$

d. $\Theta(n^2)Θ(n2).$

2.Professor Caesar wishes to develop a matrix-multiplication algorithm that is asymptotically faster than Strassen's algorithm. His algorithm will use the divide-and-conquer method, dividing each matrix into pieces of size $n / 4 \times n / 4$ , and the divide and combine steps together will take $\Theta(n^2)$ time. He needs to determine how many subproblems his algorithm has to create in order to beat Strassen's algorithm. If his algorithm creates aa subproblems, then the recurrence for the running time T(n) becomes $T(n) = aT(n / 4) + \Theta(n^2)$ . What is the largest integer value of aa for which Professor Caesar's algorithm would be asymptotically faster than Strassen's algorithm?

Strassen's algorithm has running time of Θ(nlg7). The largest integer aa such that $\log_4 a < \lg 7$ is a = 48.

3.Use the master method to show that the solution to the binary-search recurrence T(n)=T(n/2)+Θ(1) is T(n)=Θ(lgn). (See exercise 2.3-5 for a description of binary search.)

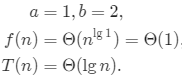
4.Can the master method be applied to the recurrence $T(n) = 4T(n / 2) + n^2\lg n$ ? Why or why not? Give an asymptotic upper bound for this recurrence.

5.Consider the regularity condition af(n/b)≤cf(n) for some constant c<1, which is part of case 3 of the master theorem. Give an example of constants a≥1 and b>1 and a function f(n) that satisfies all the conditions in case 3 of the master theorem, except the regularity condition.

a=1, b=2 and f(n)=n(2−cosn).

4.6 Proof of the master theorem

1.Give a simple and exact expression for $n_j$ in equation (4.27) for the case in which b is a positive integer instead of an arbitrary real number.

2.Show that if $f(n) = \Theta(n^{\log_b a}\lg^k{n})$ , where k≥0, then the master recurrence has solution $T(n) = \Theta(n^{\log_b a}\lg^{k + 1}n)$ . For simplicity, confine your analysis to exact powers of bb.

3.Show that case 3 of the master method is overstated, in the sense that the regularity conditionaf(n/b)≤cf(n) for some constant c < 1 implies that there exists a constant ϵ>0 such that $f(n)=\Omega(n^{\log_b a + \epsilon})$ .

Problems

1.Give asymptotic upper and lower bound for T(n) in each of the following recurrences. Assume that T(n) is constant forn≤2. Make your bounds as tight as possible, and justify your answers.

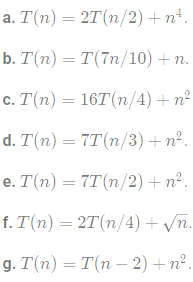
2.Throughout this book, we assume that parameter passing during procedure calls takes constant time, even if an N-element array is being passed. This assumption is valid in most systems because a pointer to the array is passed, not the array itself. This problem examines the implications of three parameter-passing strategies:

An array is passed by pointer. Time =Θ(1).
An array is passed by copying. Time =Θ(N), where N is the size of the array.
An array is passed by copying only the subrage that might be accessed by the called procedure. Time =Θ(q−p+1) if the subarray A[p..q] is passed.

a. Consider the recursive binary search algorithm for finding a number in a sorted array (see Exercise 2.3-5). Give recurrences for the worst-case running times of binary search when arrays are passed using each of the three methods above, and give good upper bounds on the solutions of the recurrences. Let NN be the size of the original problems and nn be the size of a subproblem.

b. Redo part (a) for the \MERGE-SORT algorithm from Section 2.3.1.

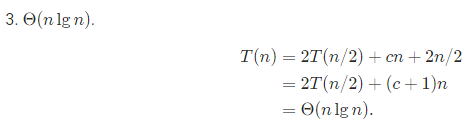
3.Give asymptotic upper and lower bounds for T(n) in each of the following recurrences. Assume that T(n) is constant for sufficiently small n. Make your bounds as tight as possible, and justify your answers.

4.Fibonacci numbers

5.Chip testing

Explanation:

If the number of chips is odd, from assumption we know the number of good chips must be greater than the number of bad chips. We randomly leave one chip alone from the chips, in which good chips are not less than bad chips.
Chip pairs that do not say each other is good either have one bad chip or have two bad chips, throwing them away doesn't change the fact that good chips are not less than bad chips.
The remaining chip pairs are either both good chips or bad chips, after throwing one chip away in every those pairs, we have reduced the size of the problem to at most half of the original problem size.
If the number of good chips is n (n>1) more than that of bad chips, we just throw away the chip we left alone when the number of chips is odd. In this case, the number of good chips is at least one more than that of bad chips, and we can eventually find a good chip as our algorithm claims.
If the number of good chips is exactly one more than that of bad chips, there are 22 cases.
- We left alone the good chip, and remaining chips are one half good and one half bad. In this case, all the chips will be thrown away eventually. And the chip left alone is the one we desire.
- We left alone the bad chip, there are more good chips than bad chips in the remaining chips. In this case, we can recursively find a good chip in the remaining chips and the left bad chip will be thrown away at the end.

c. As the solution provided in (b), we can find one good chip in

T(n)≤T(⌈n/2⌉)+⌊n/2⌋.

By the master theorem, we have T(n)=O(n). After finding a good chip, we can identify all good chips with that good chip we just found in n−1 tests, so the total number of tests is

O(n)+n−1=Θ(n).

6.Monge arrays