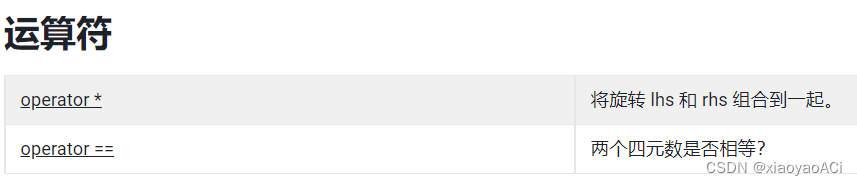
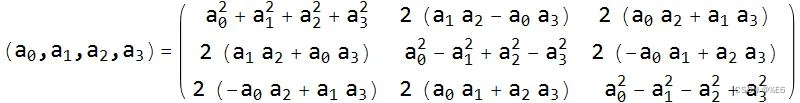相关文章
User Exits和Customer Exits
一、Extension of SAP functionality
SAP makes different possibilities available to extend SAP functionality in the R/3 without modifying the delivered R/3-Standard. Thus these extensions are further present also after a R/3-Release-Wechsel.
User exit Fi…
sql查询中使用in和exits比较和区别
首先,查询中涉及到的两个表,一个user和一个order表,具体表的内容如下: user表: order表: in 确定给定的值是否与子查询或列表中的值相匹配。in在查询的时候,首先查询子查询的表,然后…
SQL语句中exits和in的区别
一 表展示
查询中涉及到的两个表,一个user和一个order表,具体表的内容如下:
user表: order表: 二 in 演示
确定给定的值是否与子查询或列表中的值相匹配。in在查询的时候,首先查询子查询的表,…
E. Exits in Excess
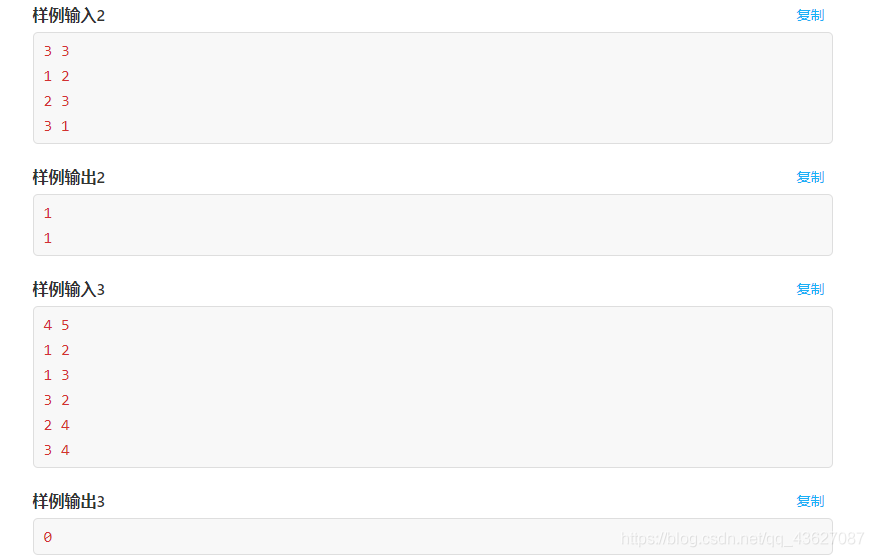
题意:
移除最多一半的边使得图没有环。 将所有边分成两部分, 第一部分为 u < v u < v u<v, 第二部分为 v > u v > u v>u, 将小的边集合删去即可。
AC代码:
int n, m;
vector<int> v1, v2…
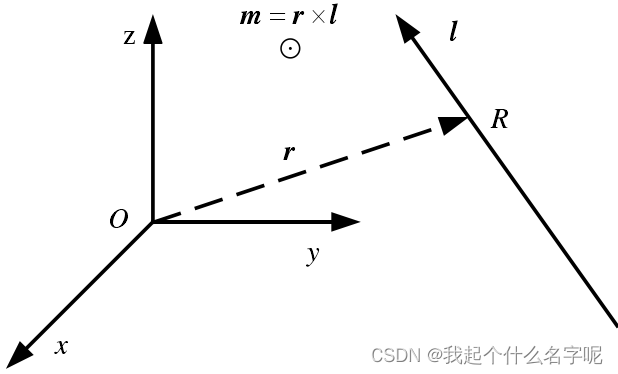
20220621 Dual Quaternion
文章目录 对偶数一、对偶数是什么?二、对偶矢量三、对偶四元数 对偶数
一、对偶数是什么?
https://zhuanlan.zhihu.com/p/358146509
对偶数是一种特殊的自洽的运算,类似于常用的复数基本单位 i i i ( i 2 − 1 i^2-1 i2−1&a…
Quaternion
01:欧拉角
1.欧拉角Vector3(x,y,z)代表的是旋转物体(若是标准旋转那么是旋转坐标轴x,y,z,转换为旋转物体则旋转角度取反顺序不变),且是将物体从物体坐标系旋转到惯性坐标系(世界坐标系中为了渲染)&#x…
Quaternion.Euler调整记录
Quaternion.Euler调整 1.运行unity 调整摄像头视角,找到需要的位置,记录下 摄像头的位置和旋转角度。 2.调整空物体的位置 使之位置与需要的位置一致 3.调整Quaternion.Euler 使Quaternion.Euler与旋转数值一致。
Quaternion(四元数)和旋转以及Yaw, pitch, roll 的含义
原文: http://www.linuxgraphics.cn/graphics/opengl_quaternion.html Quaternion(四元数)和旋转 本文介绍了四元数以及如何在OpenGL中使用四元数表示旋转。 Quaternion 的定义 四元数一般定义如下: qwxiyjzk其中 w,x,y,z是实数。同时,有…
Unity3d开发之对Quaternion的使用
上周找到了新公司。这周二来上班。可怕的是我刚去的第二天下午四点领导通知我做一个VRdemo,要求第二天交。我勒个擦。我现在对设备还没熟悉呢。连sdk都没下载而且距离上一次开发vr是在快两年之前了。属实让我措手不及。没错,按剧本走,加班到凌…
【Unity编程】四元数(Quaternion)与欧拉角
欧拉旋转、四元数、矩阵旋转之间的差异
除了欧拉旋转以外,还有两种表示旋转的方式:矩阵旋转和四元数旋转。接下来我们比较它们的优缺点。 欧拉角
优点:三个角度组成,直观,容易理解。优点:可以进行从一个方…
Quaternion类
Euler public static Quaternion Euler(float x, float y, float z); public static Quaternion Euler(Vector3 euler); 功能: 返回Quaternion对应的欧拉角 例子: public class ExampleClass : MonoBehaviour {public Quaternion rotation Quaternion.Euler(0, 30,…
Unity Quaternion
Quaternion 类的属性
eulerAngles 欧拉角
Quaternion 类的实例方法
1、SetFromToRotion 函数
2、SetLookRotation 函数
3、ToAngleAxis 函数
Quaternion 类的静态方法
1、Angle方法
2、Dot方法
3、Euler方法
4、FromToRotation方法
5、Inverse方法
6、Lerp方法
7…
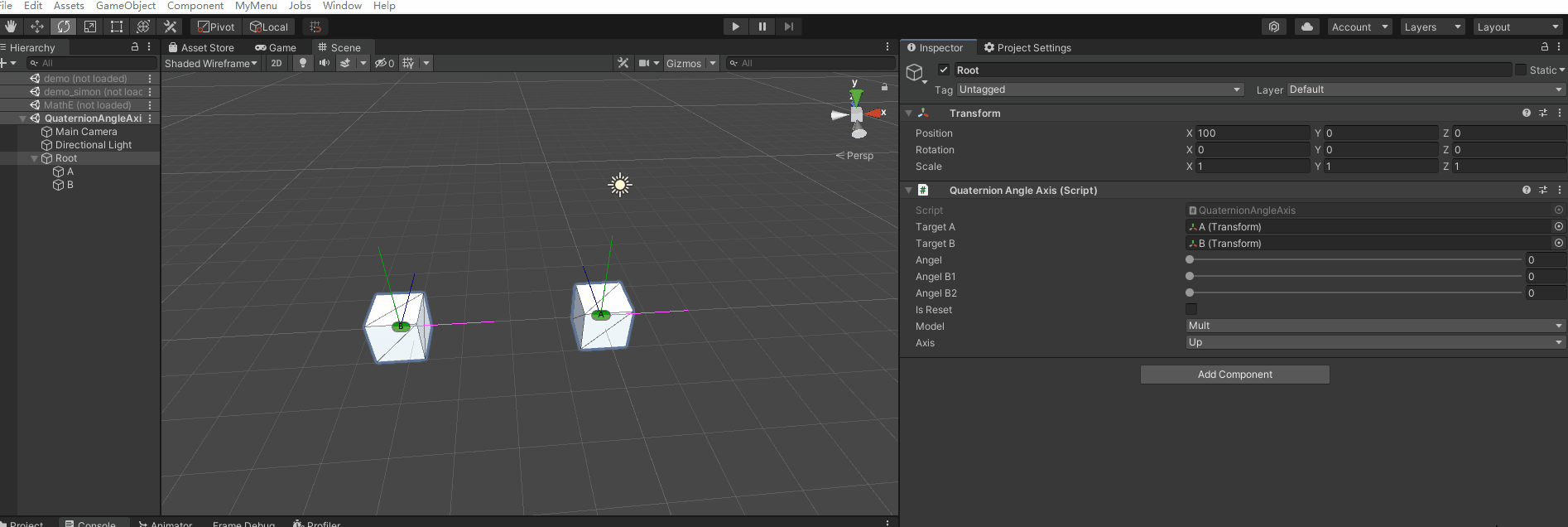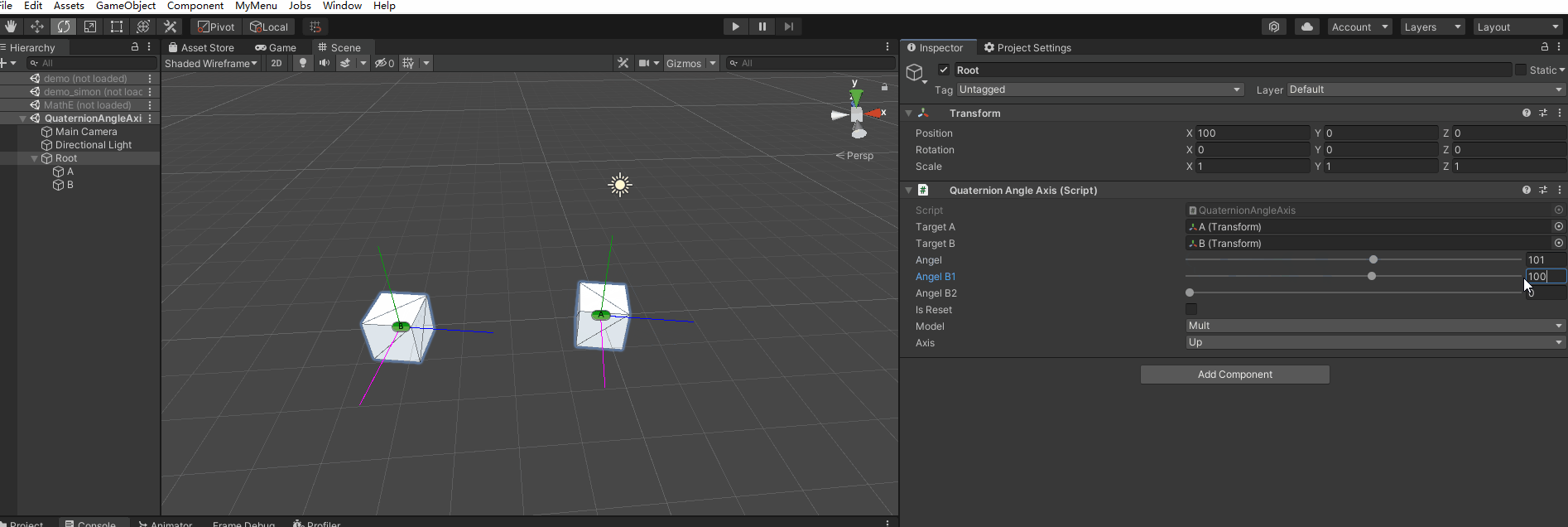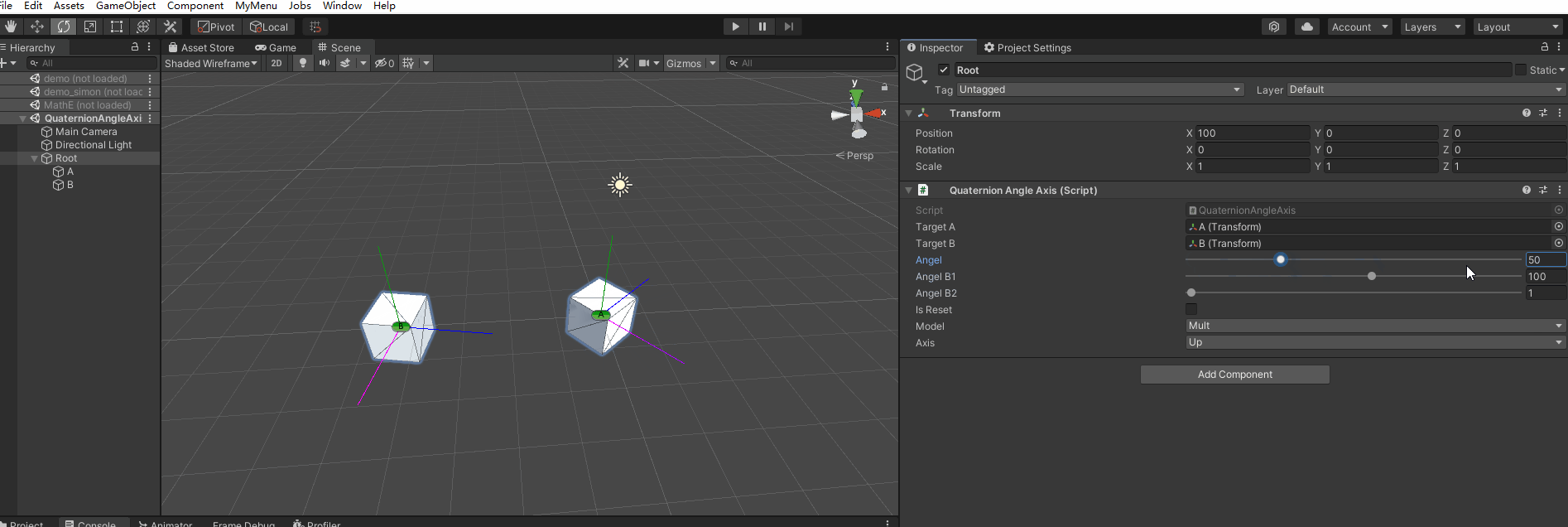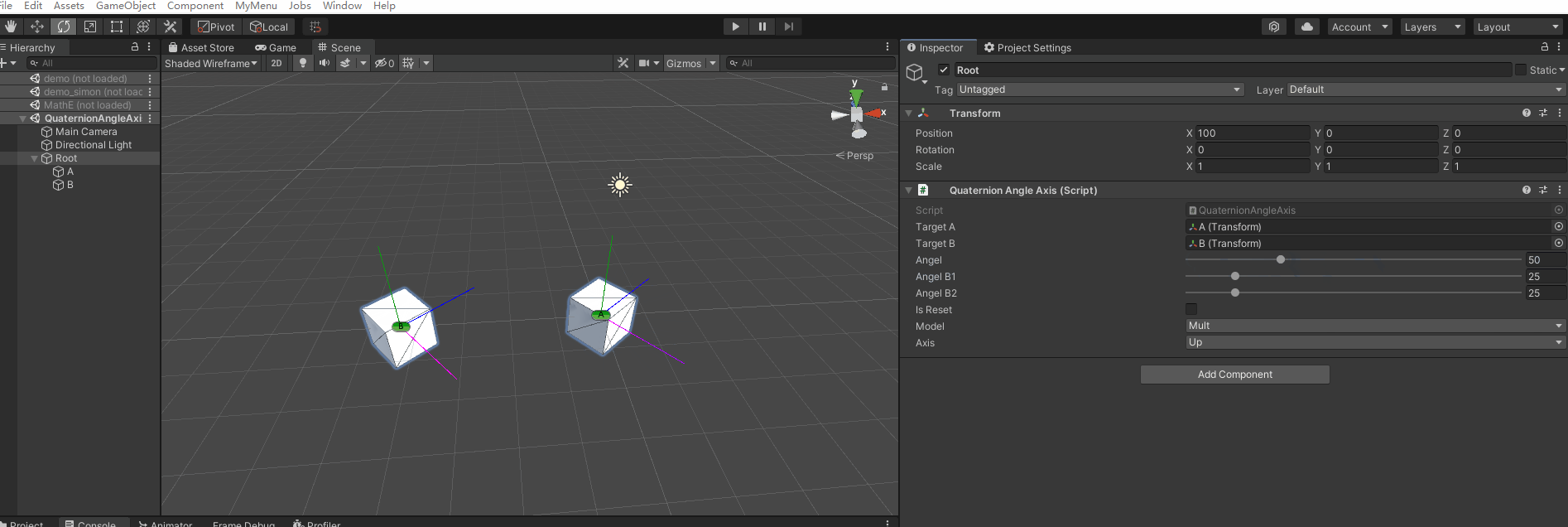
【第018问 Unity中对Quaternion.AngleAxis的理解?】
一、背景
在游戏研发过程中,有时候会对一个物体经过多次围绕不同的轴进行不同角度的旋转,从而计算得到一个方向,以此来检测在该对应的方向上是否有对应的物体或别的对象,因此本节对Quaternion.AngleAxis进行简单的记录࿱…
Unity API详解——Quaternion类
Quaternion类又称四元数,由x、y、z和w这4个分量组成,属于struct类型。在Unity中,用Quaternion来存储和表示对象的旋转角度。Quaternion的变换比较复杂,对于GameObject一般的旋转及移动,可以用Transform中的相关方法实现…
Unity3D - 详解Quaternion类[转载]
一、简介 Quaternion又称四元数,由x,y,z和w这四个分量组成,是由爱尔兰数学家威廉卢云哈密顿在1843年发现的数学概念。四元数的乘法不符合交换律。从明确地角度而言,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话&…
【Unity】Unity常用类:向量Vector3、四元数Quaternion
文章目录 Vector3构造函数静态变量变量运算符常用方法(静态)OrthoNormalize(正交标准化)Reflect(反射)Lerp(线性插值) Quaternion构造函数静态变量变量常用方法Eular(欧拉…
unity学习笔记——Quaternion(四元数)
本篇文章转自https://www.cnblogs.com/driftingclouds/p/6626183.html
Quaternion类
Quaternion(四元数)用于计算Unity旋转。它们计算紧凑高效,不受万向节锁的困扰,并且可以很方便快速地进行球面插值。 Unity内部使用四元数来表…
【Unity编程】Unity中关于四元数的API详解
Unity中关于四元数的API详解
Quaternion类
Quaternion(四元数)用于计算Unity旋转。它们计算紧凑高效,不受万向节锁的困扰,并且可以很方便快速地进行球面插值。 Unity内部使用四元数来表示所有的旋转。
Quaternion是基于复数&am…
四元数快速入门【Quaternion】
四元数(Quaternion)是用于旋转和拉伸向量的数学运算符。 本文提供了一个概述,以帮助理解在空间导航等应用程序中对四元数的需求。 推荐:用 NSDT场景设计器 快速搭建3D场景。 可以通过多种方式在空间中准确定位、移动和旋转物体。 …
四元数(Quaternion)食用指南
四元数(Quaternion)食用指南 “这简直就是黑魔法!” 开发时,每次遇到旋转问题时总会心头一震,在欧拉角和四元数这两种处理方式的选择上犹豫不决,不知不觉就陷入了四元数的淤泥中…接下来,我决定…
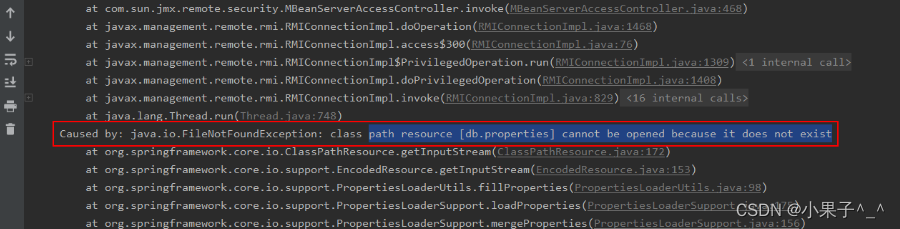
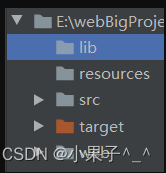









![Unity3D - 详解Quaternion类[转载]](https://img-blog.csdnimg.cn/c483c41d74754e688620c250ec1ef653.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3N1bmhhbzUyMTExMQ==,size_16,color_FFFFFF,t_70#pic_center)