四元数(Quaternion)是用于旋转和拉伸向量的数学运算符。 本文提供了一个概述,以帮助理解在空间导航等应用程序中对四元数的需求。

推荐:用 NSDT场景设计器 快速搭建3D场景。
可以通过多种方式在空间中准确定位、移动和旋转物体。 更熟悉和更容易可视化的滚动(Roll)、俯仰(Pitch)和偏航(Yaw)表示是有局限性的,在某些情况下应该用更强大的四元数代替。 随着对象的位置和方向发生变化,称为四元数的数学工具可用于旋转和缩放原始矢量。
三维空间中的物体可以定位在一个坐标系中,三个数从坐标系的原点延伸到空间中的一点,创建一个位置 r=(x,y,z) 向量。 如果对象的位置发生变化,向量将位于新的位置并且可能具有新的长度。 我们需要一种方法来测量或计算两个向量之间的变化。
1、Roll/Pitch/Yaw表示法的问题
大多数读者可能都知道,在空间中旋转的物体可以用它们沿三个轴的旋转角度来描述。 空间中的任何旋转都可以用这些旋转的组合来描述。
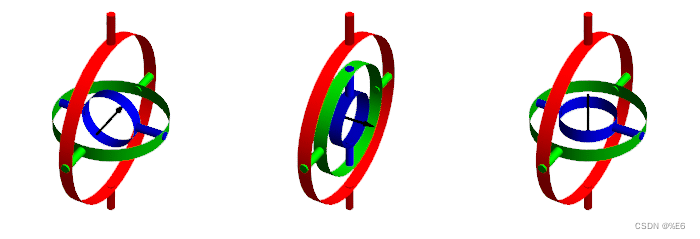
万向节提供偏航、滚动和俯仰运动。
旋转轴并不总是独立的,解也不总是唯一的。 两个万向节的平面可能会对齐,并且会发生称为万向节锁定(gimbal lock)的情况。 在万向节锁定中,三个万向节中的两个是平行或非常接近平行的,最初的三个自由度(偏航、俯仰和滚动)减少到两个自由度——两个旋转轴可以描述相同的旋转运动。 同时,失去了一个自由度,信息也消失了。 一旦发生万向节锁定,就不可能在没有外部参考的情况下重新定向轴。
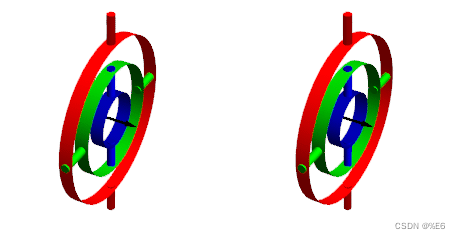
当绿色圆圈与红色圆圈对齐或接近对齐时发生万向节锁定
你可能还记得在有关阿波罗 13 号任务的电影中听到过万向节锁定这个词。 如果万向节锁定发生在爆炸之后,宇航员的惯性测量装置将无法追踪他们在天球中的位置,从而对他们本已绝望的处境产生负面影响。
现在来看看万向节锁背后的数学原理。
读者须知:为了保持在小型设备上的可读性,cos(x) 的所有实例都已替换为 Cx,sin(x) 的所有实例均已替换为 Sx。
围绕单个轴旋转一个矢量 r=(x,y,z) 需要一个旋转矩阵。 上图的三轴云台有三个轴对应三个旋转矩阵。
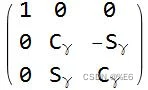
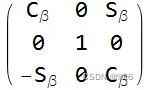

上面的三个矩阵分别表示:绕x 轴 旋转角度 γ,绕y 轴 旋转角度 β,绕z 轴旋转角度 α 。
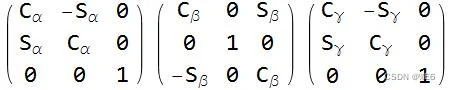
上面显示的是三个独立的 3×3 变换矩阵。 (围绕 z-y-z 旋转 α、β、γ 角度的变换)
从数学上讲,3×3 旋转矩阵是三个连续旋转的乘积。
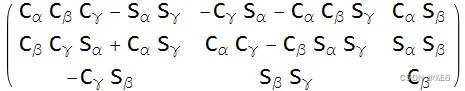
3×3 矩阵连续相乘时会产生一个 3×3 矩阵。 上面显示的是围绕 z-y-z 旋转角度 α、β、γ 。
存在多个转换矩阵,它们可以以各种顺序应用。 十二个旋转序列可以分为两类:
- 欧拉角:其中一个旋转轴重复(x-z-x,x-y-x,y-x-y,y-z-y,z-y-z,z-x-z)
- 泰特-布赖恩角,围绕所有轴(x-z-y, x-y-z、y-x-z、y-z-x、z-y-x、z-x-y)旋转
我任意选择了 z-y-x 变换矩阵来处理下面的示例。
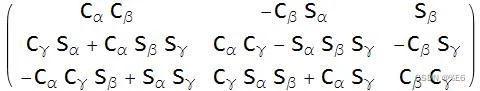
上图是围绕α、β、γ旋转z-y-x的变换矩阵。
当使用 β =π/2 代入 z-y-x 变换矩阵时,万向节锁在我们的示例矩阵中在数学上变得明显(其他变换矩阵在不同条件下失败)。随着角度 β →π /2 以及 sin(β)→0 ,您可以在下面看到对矩阵的简化效果。
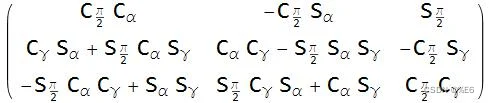
上面的矩阵中将π /2 带入β ,得到
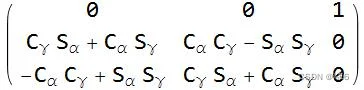
可以看到,当 β 接近 π/2 时, cos(π/2) 导致矩阵中的几项变为零。
另一种看待问题的方法是采用原始变换矩阵(我再次选择 z-y-x)并使用三角恒等式将三角函数内的变量聚集在一起。 注意角度的初始相互依赖性。
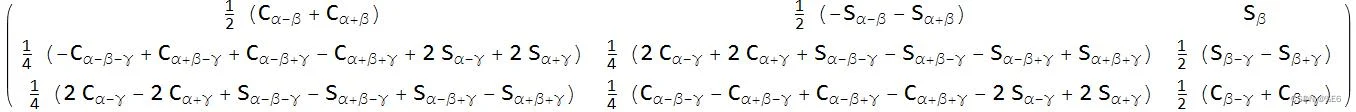
替换后,角度之间唯一存在的关系是 α + γ 。
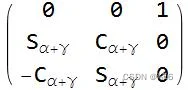
通过固定 β = π/2 ,我们已经消除了 α−γ 的所有情况,牺牲一定程度的自由度。
虽然很容易想象滚动、俯仰和偏航,但如果你正在设计一个能够自由指向空间中任何方向的系统,最终会遇到万向节锁定。
2、四元数
威廉·汉密尔顿于 1843 年发明了四元数,作为一种允许他对向量进行乘法和除法、旋转和拉伸的方法。
我在下面提出的内容旨在说明,但绝不是数学上严格的。 它应该足以让你在计算机科学和工程环境的入门级理解四元数。 对于数学课来说,这并不意味着就足够了。 如果你需要更深入的信息,加利福尼亚州立大学富勒顿分校物理学和数学教授 Alfonso Agnew 博士推荐了以下有关该主题的书籍:
- 四元数和旋转序列:在轨道、航空航天和虚拟现实中的应用入门 (Kupiers)
- Clifford 代数和旋量 (Lounesto)
- 可视化四元数 (Hanson)
汉密尔顿的发现是,虽然没有明显的方法可以将两组三个数字相乘并除以得到三个数字(可能代表坐标的向量),但可以将两组四个数字相乘并相除并得到四个 数字。 四元数是两组四个数的商,由一个标量和一个向量组成。
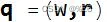
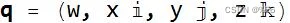
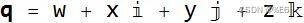
其中,
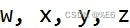
为实数,且
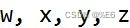
为四元数单位。
任意两点之间的方向可以用三个数表示,这三个数分别位于 (-1,1) 范围内,其总大小为 (-1 ≤ x ≤1, -1 ≤ y ≤ 1, -1 ≤ z ≤ 1)并且 √x2+y2+z^2 = 1 。这四个数字一起创建了一个描述旋转和距离的四元数。
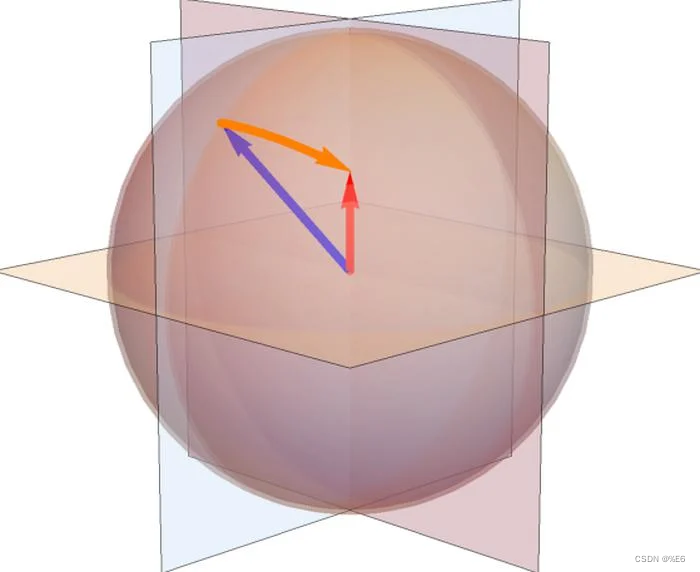
四元数提供旋转向量所需的信息,只需四个数字而不是旋转矩阵所需的九个数字。
如果你熟悉数学和矩阵符号,请跳至下面的四元数数学,并跳过接下来两节中复数和矩阵数学的复习。
3、复数
参见 AAC 教科书第 2 卷 — 第 2 章。
发明复数是为了解决没有实数解的问题。 在发明 √-1 之前 , x^2 = -1这类问题始终无解。 复数可以想象成位于一个平面上,数的实部沿水平轴表示,数的虚部沿垂直轴表示。 在笛卡尔坐标中,它们通常以类似于 x+yi 或 (x,y) 的形式表示。 两个复数可以相加、相减、相乘和相除。
相加:
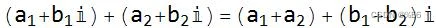
相减:
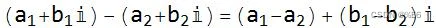
相乘:
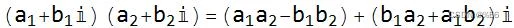
相除:
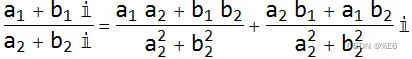
无缩放旋转:
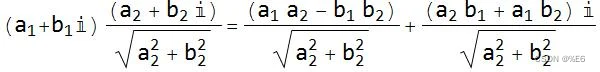
一个例子是 2+3i 逆时针旋转π/2 可以通过与 0+i 相乘得到:
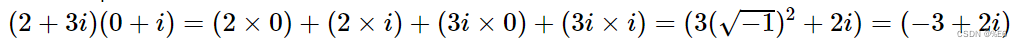
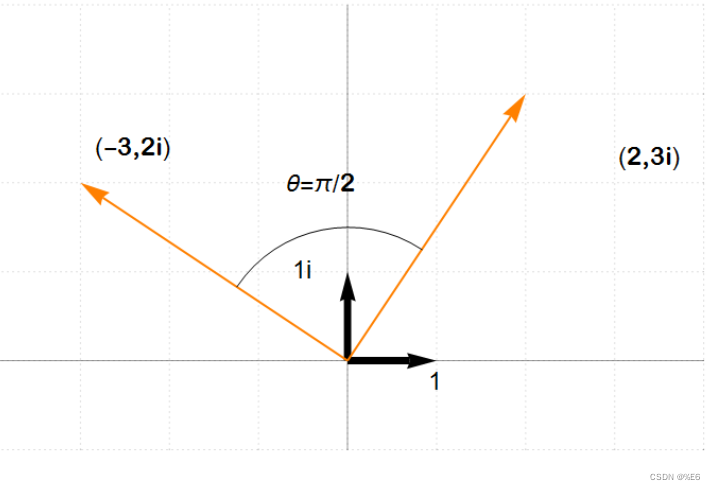
欧拉开发了一种在复数极平面中旋转复数的方法,汉密尔顿以此为基础建立了他的想法。
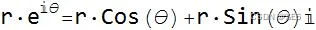
虽然这远非对复数主题的完整处理,但它通过以下方式为四元数提供了一个垫脚石:
- 复数可以很容易地进行加、减、乘和除,而无需使用三角函数(尽管复数可以用极坐标形式表示或从极坐标形式分别用 cos 和 sin 分解为实部和虚部)。
- 将复数乘以虚数单位“i”产生四分之一圈。 与四元数类似,将任意两个四元数单位相乘将导致围绕垂直于两个初始轴的轴旋转。
4、矩阵数学
- 标量
标量是表示沿公共比例尺或轴的位置的数字。 标量变量没有应用于它们的特殊格式。
- 向量
向量是一个有序数字的列表,描述了在特定方向上沿尺度的位置。 它被可视化为具有长度和方向的直线。 本文中矢量变量以粗体 r 显示,偶尔会使用上标箭头。 向量可以有两个或更多元素。
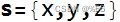
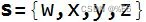
多个向量通过不同的变量名或下标来区分。
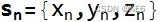
或者
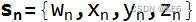
- 叉积
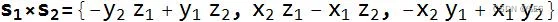
- 点积
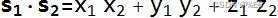
- 长度
矢量的长度是从起点到终点的直线距离。 在数学上,它是单个元素平方和的平方根。
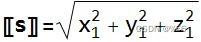
- 矩阵
矩阵是单个元素的数组,可以乘以向量以对其进行转换。 矩阵可以平移、旋转和缩放向量。 下面显示的是一个通用的 3×3 矩阵

- 矩阵应用于向量
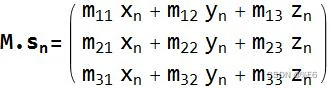
- 旋转矩阵
旋转矩阵可以改变向量指向的方向,在空间中重新定向它们。 以下矩阵围绕笛卡尔轴旋转向量而不缩放它们。
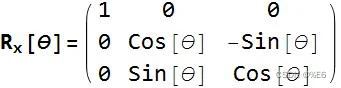
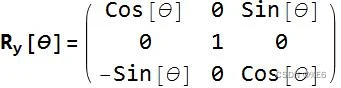
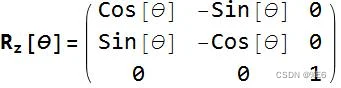
- 矩阵A与B相乘
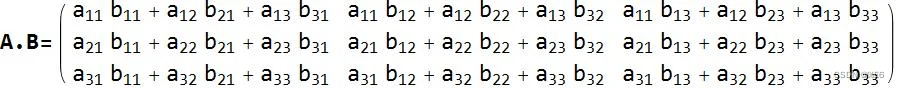
本节简要回顾向量和矩阵数学,并与下面的四元数规则进行对比。
5、四元数
如前所述,四元数由一个标量和一个向量组成。
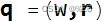
由于标量和向量都存在于四元数中,因此用于处理它们的数学规则是标量和向量数学的组合。
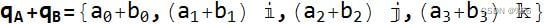
- (非交换)四元数乘法
两个四元数相乘的结果是一个新的四元数。

- 四元数内积
四元数内积是两个四元数对应的实系数相乘得到的标量。
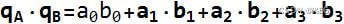
- 四元数共轭(Conjugate)
每个四元数都有一个相反数,可以通过仅对四元数的向量部分的系数求反来找到。
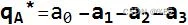
- 四元数范数(Norm)
四元数通常应始终位于单位球面上。 范数应等于 1。如果你的四元数偏离单位球体,可以将四元数的每个元素除以范数以返回单位球体。
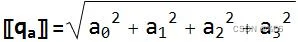
- 四元数转旋转矩阵
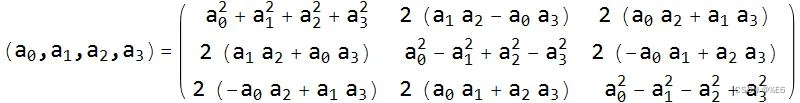
6、结束语
四元数是使用一组有序的四个数字来描述 3D 空间中的方向或旋转的另一种方法。 它们能够唯一地描述围绕任意轴的任何三维旋转,并且不会受到万向节锁定的影响。 如果你的应用程序中的传感器或物体能够在 3D 空间中的任何位置移动,那么它们在跟踪物体方面优于欧拉角。
原文链接:四元数快速指南 - BimAnt