1. mlib.linalg.distributed包

  矩阵计算是很多科学计算的重要步骤，而分布式矩阵存储则是分布式计算的基础。根据不同的计算需求，需要将用于计算的矩阵进行拆分，利用map-reduce的思想将整块矩阵的计算map成子矩阵的操作，从而得以在一个矩阵的计算步中，矩阵各部分在不同的计算单元上同步进行，最终将结果reduce汇总，从而得到计算结果。这样的矩阵分块计算针对大型矩阵运算有着很好的加速效果，而不论是GPU常见的Cuda编程还是CPU常见的MPI编程、Hadoop或Spark编程，都需要矩阵分块存储运算这一关键功能。
  Spark的mlib库所使用的分布式矩阵，均在 spark.mlib.linalg.distributed 包内，接下来的内容就将对distributed包内的各种不同分块矩阵形式的创建和操作进行 源码级 的详细介绍。

2. DistributedMatrix特质

  DistributedMatrix特质是distributed包中仅有的一个特质，也就是类似Java中的接口类，而这个类也十分简单，只定义了两个返回行列数的抽象类和一个返回Breeze库中DenseMatrix类的toBreeze私有抽象类，这些都将被接下来介绍的数个分布式矩阵存储形式类继承并实现。

3. BlockMatrix类

  BlockMatrix是分布式矩阵存储中最常用的类型，它将矩阵按行列分块存储，而这样的存储形式对常见的矩阵运算都能提供很好的支持。我们先来看一下BlockMatrix的两个构造函数：

// BlockMatrix主构造函数
new BlockMatrix(blocks: RDD[((Int, Int), Matrix)], rowsPerBlock: Int, colsPerBlock: Int, nRows: Long, nCols: Long)
// BlockMatrix辅助构造函数
new BlockMatrix(blocks: RDD[((Int, Int), Matrix)], rowsPerBlock: Int, colsPerBlock: Int)

  可以看到，BlockMatrix的主构造函数和辅助构造函数都需要以一个 RDD[((Int, Int), Matrix)] 类型的矩阵数据输入和两个 Int 型的矩阵信息输入，而主构函数增加了两个 Long 型矩阵整体行列数的定义，我们看一下主构造函数的文档解释：

  blocks 所需的RDD类型 RDD[((Int, Int), Matrix)] 是原矩阵的一个子分块矩阵，第一个两个Int构成的元组分别标示了该子分块矩阵在原矩阵总分块中的行列标，而第二个Matrix类则是可以向下兼容DenseMatrix和SparseMatrix的子分块矩阵。【DenseMatrix与SparseMatrix的创建与操作】
  由此可见，BlockMatrix的存储如图所示：

  这样的矩阵分块形式经常会存在一个问题，当分到最后一行和最后一列时，行列数无法满足给定的 rowsPerBlock 和 colsPerBlock 。而从官方文档中可以看出，构造函数的这两个数值允许在最后一行和最后一列的子矩阵中不满足，从而在创建时就不用担心矩阵分块所产生的不满矩阵问题。
  了解完构造函数，就让我们看看BlockMatrix都有哪些可用的操作方法：

1. add(other: BlockMatrix): BlockMatrix
2. subtract(other: BlockMatrix): BlockMatrix

  相加 / 相减方法【传入另一个BlockMatrix，返回BlockMatrix为两个矩阵之和 / 之差】：是的是相加相减！连DenseMatrix和SparseMatrix这两个矩阵基本存储类都没有的相加方法竟然在分布式矩阵中创建了操作方法。（DenseMatrix和SparseMatrx在编写时想实现矩阵相加还是有多种方法的，这个会在之后的文章中讲述）

3. blocks: RDD[((Int, Int), Matrix)]

  提取子矩阵RDD方法【直接调用，返回构成BlockMatrix的子矩阵RDD】

4. cache(): BlockMatrix.this.type

  缓存操作【直接调用，将该分块矩阵进行缓存】：
  缓存这个概念比较特殊，我需要单独拿出来讲一下。

•  首先，为什么要缓存？ 这个跟Spark的运行机制有关。分布式系统在节点计算上一定要设计足够的容错机制，避免个别节点的问题导致整个计算任务的计算失败，所以Spark在将task分配到executor执行时，会将对RDD的操作，也就是RDD间的依赖关系进行保存，特别针对窄依赖而言，由于其可以在多个计算节点上互不相干地并行执行，所以通过对窄依赖的保存可以在某一节点执行task失败时，通过窄依赖重新计算RDD，甚至交由其它节点代替执行。
   但是如果这个task内的RDD算子计算十分复杂或步骤较多，计算开销巨大，则在这个task中执行完某些计算开销巨大的RDD算子之后对RDD进行缓存，则可以在之后某个算子执行失败后的重新计算中，从缓存过的RDD开始，而不必从头计算，相当于在依赖关系中加入缓存操作，改变了缓存操作前后依赖关系的数据流向和数据源，从而减少由于计算任务失败而重新计算带来的计算开销。
•  其次，如何缓存？ 在Spark中，对RDD的缓存有两种方式，分别是 presist() 和 cache()，而在底层其实 cache 也调用了 presist() ，只不过通过传参 MEMORY_ONLY 使得对象只缓存在JVM的堆内存中，但实际上 presist() 还提供了多中缓存的方式，可以选择缓存在 MEMORY内存 、 DISK磁盘 或 OFF_HEAP堆外系统内存（方便用户规避GC垃圾回收无法手动回收的不足） 等多种存储区域，也可同时选择多种。
   缓存保存在内存中可能存在内存被覆盖或清理的风险，同时如果计算节点挂掉了内存中的缓存RDD也将失效，重做这份task将按照依赖关系重新计算。想要减少内存缓存带来的风险，可以使用文件系统将缓存持久化，也就是保存在磁盘中，如果使用HDFS文件管理系统则在集群中会存在多个副本，也将增加容错的效率。Spark中通过 SparkConf().setCheckpointDir() 设定持久化缓存的文件路径，再通过 RDD.checkpoint() 即可将缓存持久化到文件中，而之后算子的依赖关系将从缓存位置开始，不再继承缓存前的所有算子。当Spark需要读取被缓存过的RDD数据时，读取缓存的操作是自动的，不需要显式指定。
   注：所有类型的缓存操作都是延迟执行的，只有遇到之后的算子才会执行缓存。
   那么 BlockMatrix 所提供的缓存机制是哪一种呢？
  
   可以看出，它直接调用了RDD的 cache() 方法，而这种方法在RDD中正是使用JVM的堆内存空间进行缓存的，这样的缓存方式使得缓存性能得以提高。
  

5. persist(storageLevel: StorageLevel): BlockMatrix.this.type

  缓存操作【输入缓存等级，将该分块矩阵进行缓存】：
  前面的 cache() 方法只能将分块矩阵默认存储在JVM的堆内存中，而这个 persist() 方法和Spark的 presist() 方法一样，将可以指定缓存的等级，也就是缓存的介质区域，我们大胆猜测这个方法同 cache() 方法一样直接调用了RDD的方法，让我们进入源码一探究竟：

  可以看到，确实调用的还是RDD的 presist() 方法，那么这个存储等级有哪些？分别有什么作用呢？

  经过多次的调用跳转，最终来到了 StorageLevel 类，其中定义了我们所能指定的所有存储级别的常量值，由此我们可以根据自己需求选择缓存的存储区域。

6. colsPerBlock: Int 	//返回每块子矩阵的列数，最后一列可能不满足
7. rowsPerBlock: Int 	//返回每块子矩阵的行数，最后一行可能不满足
8. numColBlocks: Int 	//返回矩阵的列分块数
9. numRowBlocks: Int 	//返回矩阵的行分块数
10. numCols(): Long		//返回矩阵总列数
11. numRows(): Long		//返回矩阵总行数

  矩阵一系列基本参数的查询操作【直接调用，返回相应查询值】

12. multiply(other: BlockMatrix, numMidDimSplits: Int): BlockMatrix
13. multiply(other: BlockMatrix): BlockMatrix

  矩阵乘法操作【输入另一个分块矩阵，并输入一个矩阵乘法中间操作的分割数，返回得到一个分块矩阵结果】：
  这个矩阵乘法既是矩阵运算中的重要操作，又因为这个分割数的加入使得这个 multiply() 方法有很多的说头，这里就着重展开这个矩阵乘法。

•  multiply(other: BlockMatrix)的调用：
    首先，先来看一下这个 multiply(other: BlockMatrix) 方法的底层：
  
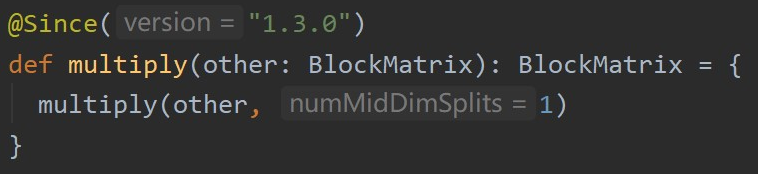
    可以看出 multiply(other: BlockMatrix) 最终还是调用了 multiply(other: BlockMatrix, numMidDimSplits: Int) 方法，并且令 numMidDimSplits 等于1，那么关键的就在这个 numMidDimSplits 这个参数究竟是什么含义呢？
•  numMidDimSplits的实际意义：
    一开始我也一脸疑惑，先看看官方文档中对这个参数的解释：
  
    根据官方解释，这个 numMidDimSplits 是为了提高并行度，主要用于乘法操作中“中间维度”的切分。这个“中间维度”是什么呢？让我们再次进入Spark的源码，在 multiply(other: BlockMatrix, numMidDimSplits: Int) 的方法中，除了有三处使用了 numMidDimSplits 这个参数：
  
  
  
    第一张图中可以看出，这个参数必须是一个大于0的整数，这也符合切分的定义，而第三张图可以很明显看出， numMidDimSplits 直接关系到partitions的数量，而partitions的数量在足够executor的情况下，就是整体并行计算的并行度，所以可以看出， numMidDimSplits 确实直接影响到计算的并行度。那么第二张图究竟是在干什么呢？进入源码：
  
  
    从源码中我们可以看出 numMidDimSplits 的真正用途，在矩阵乘法A x B中，分块矩阵乘法结果矩阵中每个子矩阵是A的一个行分块与B的一个列分块相乘得到的结果，而在Spark的mlib中，两个矩阵乘法所产生的task数正是这行列相乘的次数，即将每一个行列相乘在一个计算单元上处理，如果A的行列分块数是m x n，B的行列分块数是n x k，则task的个数，也就是并行度为m x k，当引入 numMidDimSplits 后并行度增加为m x k x numMidDimSplits，实则对A的行子矩阵与B的列子矩阵进行矩阵乘时，再按 numMidDimSplits 的个数对A的行子矩阵和B的列子矩阵进行拆分，从而将每一个A的行子矩阵和B的列子矩阵的乘法拆分成 numMidDimSplits 个矩阵乘法，通过对A的列索引对 numMidDimSplits 取余和B的行索引对 numMidDimSplits 取余可以得到每个子矩阵在再次拆分后的每个计算子块中的下标，实现对矩阵乘法运算更大的并行加速。实际操作如下图所示：
  
    对分布式并行矩阵乘法再次分块并行，从而使得并行度增加，这是 numMidDimSplits 这个参数的主要意义，而官方文档中所说的矩阵乘法的中间维度，正是矩阵乘法行列子矩阵相乘的这个中间过程，这也就很好理解这个参数名字的意义了。
•  multiply方法的其它注意事项（A x B矩阵乘法）：
    1）A矩阵（主调矩阵）的每块列数必须等于B矩阵（被调矩阵）的每块行数。
    2）如果B矩阵为稀疏矩阵，则会自动转化为稠密矩阵进行计算，并且保存的结果分块矩阵也会是稠密矩阵存储形式。但这样的操作会带来一定性能缺陷，暂时还不支持两个稀疏矩阵直接相乘。

14. toCoordinateMatrix(): CoordinateMatrix
15. toIndexedRowMatrix(): IndexedRowMatrix

  矩阵转换操作【直接调用，返回与原矩阵等效的协调矩阵 / 带索引的行矩阵】

16. toLocalMatrix(): Matrix

  矩阵转换操作【直接调用，对分布式分块矩阵进行collect操作，获得一个等效的稠密矩阵】

17. transpose: BlockMatrix

  矩阵转置操作【直接调用，返回原矩阵转置后的矩阵】

18. validate(): Unit

  矩阵验证操作【直接调用，对矩阵进行验证？验证失败会报错（这个地方我还不是太明白验证什么……以后有用到的话好好研究一下）】

4. CoordinateMatrix类

  CoordinateMatrix是存储稀疏矩阵的分布式矩阵类，先来看看它的构造函数：

// 主构造函数
new CoordinateMatrix(entries: RDD[MatrixEntry], nRows: Long, nCols: Long)
// 辅助构造函数
new CoordinateMatrix(entries: RDD[MatrixEntry])

  这种分布式矩阵类型相对简单，存储的基本元素是 MatrixEntry ，这个 MatrixEntry 只有三个元素构成：

  而它的矩阵操作方法也十分的简单：

1. entries: RDD[MatrixEntry] //返回矩阵Entry元素
2. numCols(): Long //返回矩阵列数
3. numRows(): Long //返回矩阵行数
4. toBlockMatrix(rowsPerBlock: Int, colsPerBlock: Int): BlockMatrix //按每块内行列数，转换为分块矩阵
5. toBlockMatrix(): BlockMatrix //以默认每块1024行x1024列，转换为分块矩阵
6. toIndexedRowMatrix(): IndexedRowMatrix //转化为带索引的行矩阵
7. toRowMatrix(): RowMatrix //转化为行矩阵
8. transpose(): CoordinateMatrix //转置，并返回转置后的协调矩阵

5. IndexedRowMatrix类

  IndexedRowMatrix是带下标的行矩阵。带下标的分布式行矩阵有着许多特殊的计算方法，我们先看一下 IndexedRowMatrix 类的构造方法：

// 主构造函数
new IndexedRowMatrix(rows: RDD[IndexedRow], nRows: Long, nCols: Int)
// 辅助构造函数
new IndexedRowMatrix(rows: RDD[IndexedRow])

  在构造函数中，主要构成矩阵的RDD类型是 IndexedRow 类型，该类型只有两个成员：

  这也能看出带下标的行矩阵这个定义，其存储的实质上是每一个行标及其行向量，而这个行向量在许多计算方法中可以提供很大的计算便利。行矩阵也提供了许多分块矩阵中所没有的封装计算方法，接下来让我们看一下带下标的分布式行矩阵所提供的调用方法：
  一些常见方法：

1. numCols(): Long //返回矩阵列数
2. numRows(): Long //返回矩阵行数
3. rows: RDD[IndexedRow] //返回带下标的行向量
4. toBlockMatrix(rowsPerBlock: Int, colsPerBlock: Int): BlockMatrix //按给定每块行列数转化为分块矩阵
5. toBlockMatrix(): BlockMatrix //按默认行列数转化为分块矩阵
6. toCoordinateMatrix(): CoordinateMatrix //转化为协调矩阵
7. toRowMatrix(): RowMatrix //转化为行矩阵

  这些常用方法所提供的作用与其它矩阵类的相似方法无异，接下来将介绍一些 IndexedRowMatrix 所拥有的独特方法，这些方法拥有其独特的数学作用，因为暂时没有用到所以还对其了解不深，目前先列出来方法和其官方文档，今后若有更为深入的研究将在撰文详述：

// 计算矩阵列之间的余弦相似性
8. columnSimilarities(): CoordinateMatrix

// 计算格拉姆矩阵
9. computeGramianMatrix(): Matrix

// 计算矩阵的奇异值分解
10. computeSVD(k: Int, computeU: Boolean = false, rCond: Double = 1e-9): SingularValueDecomposition[IndexedRowMatrix, Matrix]

6. RowMatrix类

  相比于 IndexedRowMatrix ， RowMatrix 拥有更多更丰富的数学运算操作方法，本小节将大致罗列这些方法，暂不细致展开，在以后的文章中我将继续从 源码级 的讲解陆续揭开这些方法的底层奥秘！
  首先，仍然让我们先看看分布式行矩阵的构造函数：

// 主构造函数
new RowMatrix(rows: RDD[Vector], nRows: Long, nCols: Int)
// 辅助构造函数
new RowMatrix(rows: RDD[Vector])

  分布式行矩阵以mlib中的向量作为基础，以矩阵每一行单独存储，其同样提供了许多常见的矩阵方法：

1. numCols(): Long //返回矩阵列数
2. numRows(): Long //返回矩阵行数
3. multiply(B: Matrix): RowMatrix //矩阵乘法
4. rows: RDD[Vector] //返回矩阵行向量

  是的没有看错，分布式行矩阵的基本方法之后这些，而更加丰富的则是作为矩阵所拥有的各种数学方法和算法，接下来将仅以介绍为主，将在以后的文章中展开：

5. columnSimilarities(threshold: Double): CoordinateMatrix// 使用抽样方法计算矩阵列之间的相似性
6. columnSimilarities(): CoordinateMatrix// 使用计算归一化点积的蛮力方法计算该矩阵列之间的所有余弦相似性
7. computeColumnSummaryStatistics(): MultivariateStatisticalSummary// 计算按列的汇总统计信息
8. computeCovariance(): Matrix// 计算协方差矩阵，将每一行视为一个观察值
9. computeGramianMatrix(): Matrix// 计算格拉姆矩阵
10. computePrincipalComponents(k: Int): Matrix// 只计算最上面的k个主成分
11. computePrincipalComponentsAndExplainedVariance(k: Int): (Matrix, Vector)// 计算最上面的k个主成分和由每个主成分解释的方差比例向量
12. computeSVD(k: Int, computeU: Boolean = false, rCond: Double = 1e-9): SingularValueDecomposition[RowMatrix, Matrix]// 计算该矩阵的奇异值分解
13. tallSkinnyQR(computeQ: Boolean = false): QRDecomposition[RowMatrix, Matrix]// 计算行矩阵的QR分解

7. 小结

  本章阐述的重点在矩阵乘法性能较优的 BlockMatrix 上，在项目实践中，根据计算的需求不同，灵活应用不同的分布式矩阵存储形式，能够减少我们的代码实现难度，同时能够带来更好的性能表现。通过对源码的分析，我们更能从中知道这些优秀的开源架构的底层原理，从而更好地将需要的地方为我们所用，将不合适的地方进行深度地定制和修改。今后的文章还将探究Spark的Mlib这个神奇的科学计算库中更多的奥秘！