实验原理：

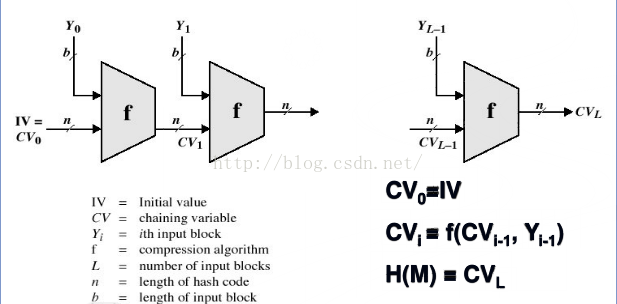
生日攻击：输入为生成元a的阶p-1和元b，输出为离散对数。设置两个长度为p的列表：

1）列表1包含，通过随机选取p个k得到；                                                                         

 2）列表2包含，通过随机选取p个l得到；                                                                     

则在两个列表中很有可能出现重复的项，即，因此，那么就是要找的离散对数。

生日攻击是一个概率算法，无法保证一定能得到输出结果。

实验内容：

 a.简单的同余函数的构造

int tongyu(int a,int m,int n){//递归原理 long long int temp=a%n,ans;if(m==1){ans=temp;}else if(m>=2){ans=(temp*tongyu(a,m-1,n))%n;}return ans;
}

 原理：(a*b)mod c=((a mod c)*(b mod c))mod c

这里是，m逐步减小，直到1

但是这个顶多m为10000多，再多就不能运行了，而我们如果需要计算很大的m，就需要分解计算

b.对较大数字的拆分

void chaifen(int a,int b[10]){//把a按照万，千，百，十，个位上的数字区分开来，便于计算 int i,temp=10000;for(i=0;i<5;i++){b[i]=a/temp;a=a%temp;temp/=10;}
}

数组b是用来储存a的万位，千位，百位，十位，个位上的值

类似于水仙花数的处理

c.求a的10000，1000，100，10，1的次方的mod p

void qiu_cd(int c1[10],int a,int p){int temp=10000;for(int i=0;i<5;i++)//求对于a的10000,1000等次方对于p的求余 {c1[i]=tongyu(a,temp,p);temp/=10;}}

d.对a的万位，千位，百位，十位，个位的值的次方分别求余

void cheng(int p,int c1[10],int c11[10],int c111[10]){//各位上的数字的求余 for(int i=0;i<5;i++){if(c11[i]>0){c111[i]=tongyu(c1[i],c11[i],p);}else{c111[i]=0;}}
}

如果c11[i]=0，直接置0，否则就用用到tongyu函数，(a*b)mod c=((a mod c)*(b mod c))mod c

 e.对a各个位的值整合起来

long long int result_c(int a, int c1[10],int p,int c11[10],int c111[10]){//输出列表的值 long long int temp=1; chaifen(a,c11);cheng(p,c1,c11,c111);for(int j=0;j<5;j++){//万位到个位上的求余结合起来 if(c111[j]!=0){temp=((temp%p)*(c111[j]%p))%p;			}}return temp;
}

也是利用那个公式(a*b)mod c=((a mod c)*(b mod c))mod c

但是c111[j]=0不能带进去，因为会使得一个乘数为0，整体为0

f.构造列表并比较

void bijiao(int p,int a, int b,int p1,long long int c[15000][2],unsigned long long int ans,long long int d[15000][2],int c1[10],int c11[10],int c111[10],int count){int flag=0;for(int i=0;i<p1;i++){//求第一个列表 c[i][0] = 1+ rand() % (p-2);c[i][1] = result_c(c[i][0],c1,p,c11,c111);}for(int i=0;i<p1;i++){//求第二个列表 d[i][0] = 1+ rand() % (p-2);ans=result_c(d[i][0],c1,p,c11,c111);ans=((b%p)*ans)%p;d[i][1]=ans;}for(int i=0;i<p1;i++){		for(int j=0;j<p1;j++){if(c[i][1]==d[j][1]){//如果找到 cout<<"能找到离散对数x="<<c[i][0]-d[j][0]<<"(mod "<<p-1<<")"; flag=1;break;}}if(flag==1){//如果找到了，跳出循环 break;}}count++;if(count>10){//超过十轮，还是没找到 cout<<"找不到";flag=1;}if(flag==0){bijiao(p,a,b,p1,c,ans,d,c1,c11,c111,count);}
}

rand是随机数，rand()%(b)，表明随机生成0-b之间的数字

两个for循环找相同值，找不到继续找，进入下一轮，再次调用bijiao函数，如果找了十轮还没找到，就说明真的很难找，建议不找，找到了通过flag跳出两个for循环。

g.总函数

#include<iostream>
#include<stdlib.h>
#include<time.h>
#include<math.h>
using namespace std;
int tongyu(int a,int m,int n){//递归原理 long long int temp=a%n,ans;if(m==1){ans=temp;}else if(m>=2){ans=(temp*tongyu(a,m-1,n))%n;}return ans;
}void cheng(int p,int c1[10],int c11[10],int c111[10]){//各位上的数字的求余 for(int i=0;i<5;i++){if(c11[i]>0){c111[i]=tongyu(c1[i],c11[i],p);}else{c111[i]=0;}}
}void chaifen(int a,int b[10]){//把a按照万，千，百，十，个位上的数字区分开来，便于计算 int i,temp=10000;for(i=0;i<5;i++){b[i]=a/temp;a=a%temp;temp/=10;}
}void qiu_cd(int c1[10],int a,int p){int temp=10000;for(int i=0;i<5;i++)//求对于a的10000,1000等次方对于p的求余 {c1[i]=tongyu(a,temp,p);temp/=10;}}long long int result_c(int a, int c1[10],int p,int c11[10],int c111[10]){//输出列表的值 long long int temp=1; chaifen(a,c11);cheng(p,c1,c11,c111);for(int j=0;j<5;j++){//万位到个位上的求余结合起来 if(c111[j]!=0){temp=((temp%p)*(c111[j]%p))%p;			}}return temp;
}
void bijiao(int p,int a, int b,int p1,long long int c[15000][2],unsigned long long int ans,long long int d[15000][2],int c1[10],int c11[10],int c111[10],int count){int flag=0;for(int i=0;i<p1;i++){//求第一个列表 c[i][0] = 1+ rand() % (p-2);c[i][1] = result_c(c[i][0],c1,p,c11,c111);}for(int i=0;i<p1;i++){//求第二个列表 d[i][0] = 1+ rand() % (p-2);ans=result_c(d[i][0],c1,p,c11,c111);ans=((b%p)*ans)%p;d[i][1]=ans;}for(int i=0;i<p1;i++){		for(int j=0;j<p1;j++){if(c[i][1]==d[j][1]){//如果找到 cout<<"能找到离散对数x="<<c[i][0]-d[j][0]<<"(mod "<<p-1<<")"; flag=1;break;}}if(flag==1){//如果找到了，跳出循环 break;}}count++;if(count>10){//超过十轮，还是没找到 cout<<"找不到";flag=1;}if(flag==0){bijiao(p,a,b,p1,c,ans,d,c1,c11,c111,count);}
}
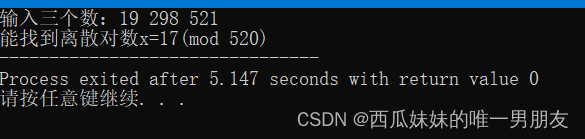
int main(){int a,b,p,p1,count=0;unsigned long long int ans=0;//p1为p的开方，ans中间值，count为轮数 long long int c[15000][2],d[15000][2];//c,d为两个列表 int c1[10],c11[10],c111[10];//c1为求a的10000等对p的余，c11为随机数的各个位上的数，c111为各个位上余数的集合 cout<<"输入三个数：";cin>>a>>b>>p;p1=int(sqrt(p));//求关于p的开方 qiu_cd(c1,a,p);//求c1 bijiao(p,a,b,p1,c,ans,d,c1,c11,c111,count);return 0;
}

h.测试结果