Overview：

1.数据表示的目的（略）

2.数值数据的表示

3.非数值数据的表示

4.数值信息的校验（重点）

---

1.数据表示的目的：

组织数据，方便计算机硬件使用（汇编语言也具有数据类型）

2.数值数据的表示

2.2 数值数据的表示方法

十进制（D—decimal）二进制（B—binary） 八进制（O—octal）十六进制（H—hexadecimal）

编码特点：

进制的表示：

基数：r

位权：Di

进制的转换：

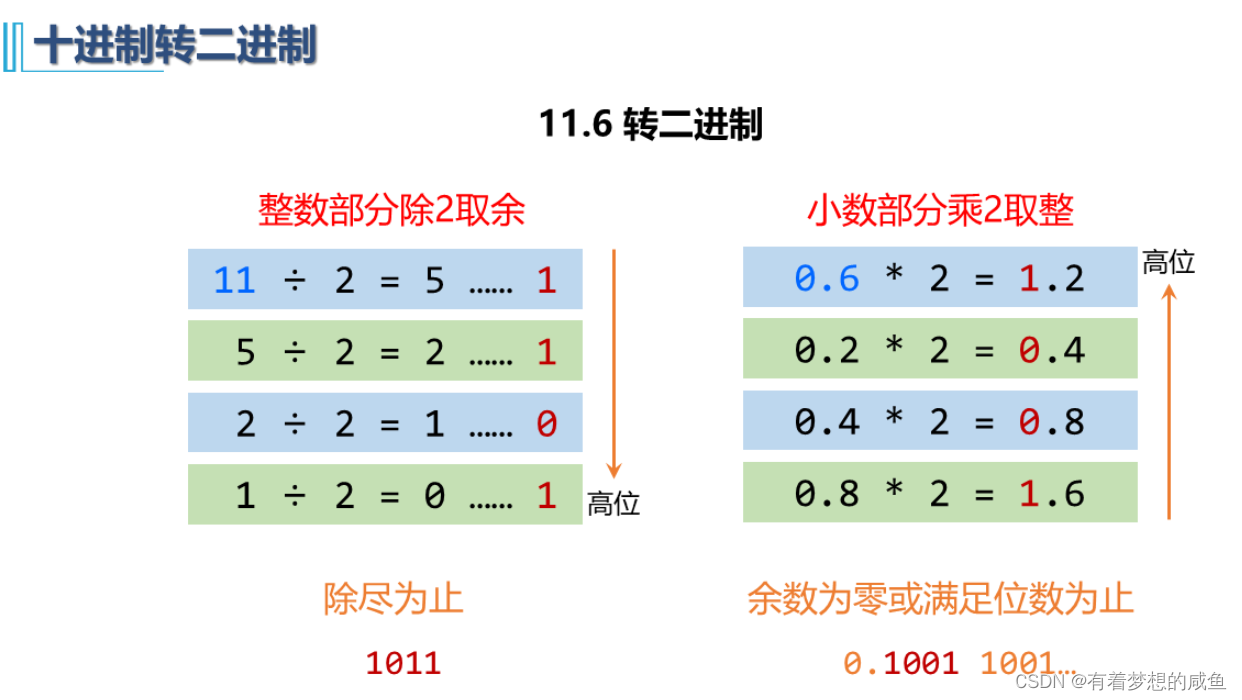
数的定点浮点表示方法

定点表示：即小数点位置固定的数

缺点：只能表示纯小数或者纯整数

定点整数：

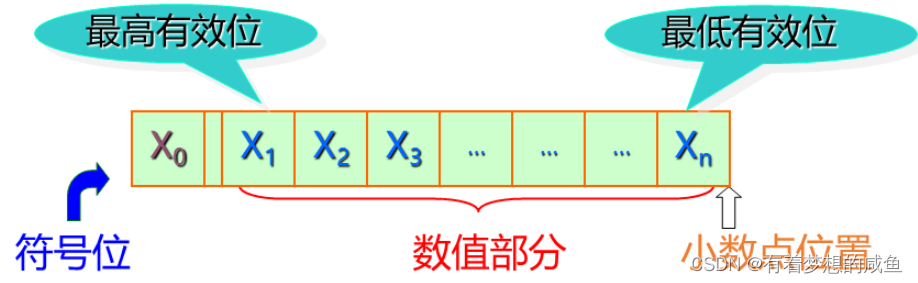
 定点小数：

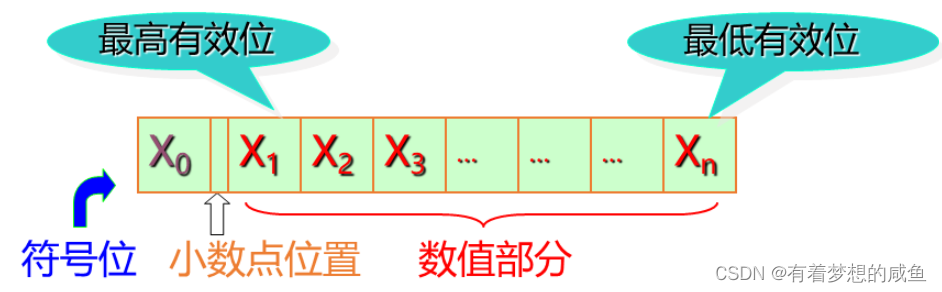
 机器数/码：

真值：即书写格式

因为机器不能识别真值（负数），所以会将符号数值化，供机器内部使用。

四种机器码：

• 原码
• 反码
• 补码
• 移码

原码：最高位为符号位，0：正  1：负

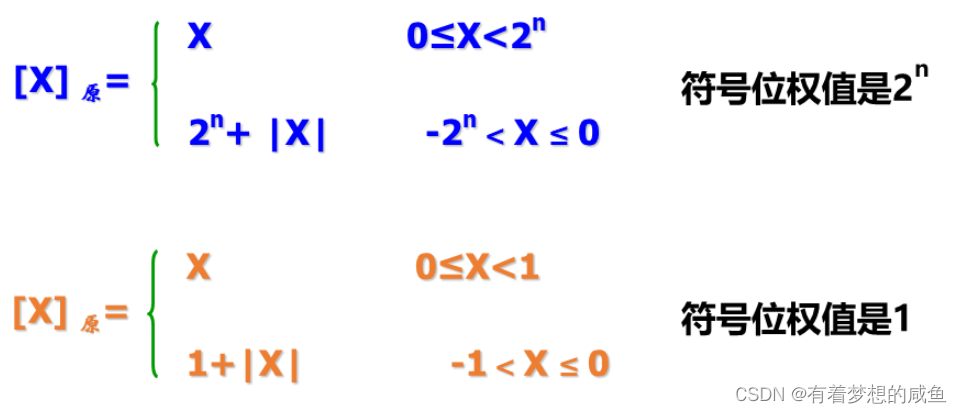
 反码：（One's  Complement）二进制的各位取反（符号位除外）

 

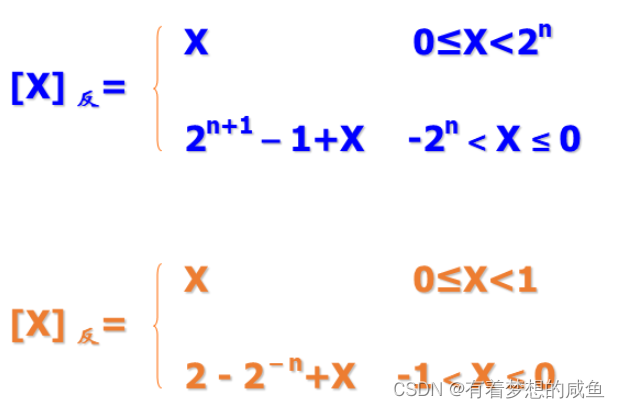
 补码：

• 真值为正——补码为原码
• 真值为负——补码为反码+1（模-真值）

补码编码方法：

零：只有补码的零为唯一表示

	原码	反码	补码
+0	0000 0000	0000 0000	0000 0000
-0	1000 0000	1111 1111	0000 0000

补码的特性：

 移码：一般用于浮点数的阶码

浮点数的表示方法：

 浮点数的表示范围：

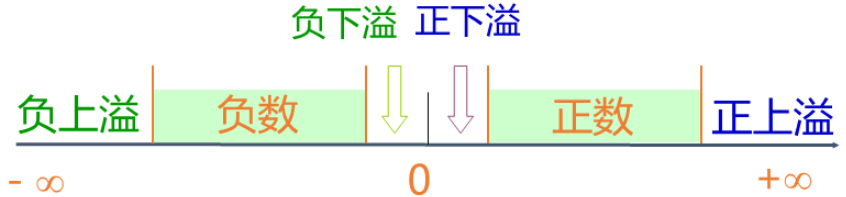
 浮点数的规格化：尾数真值最高位为1的数称为规格化数

规格化方法：

• 左规：尾数左移，阶码变小
• 右规：尾数右移，阶码变大

浮点数IEEE754：

 阶码：为什么E = e + 127（偏移量）是127？