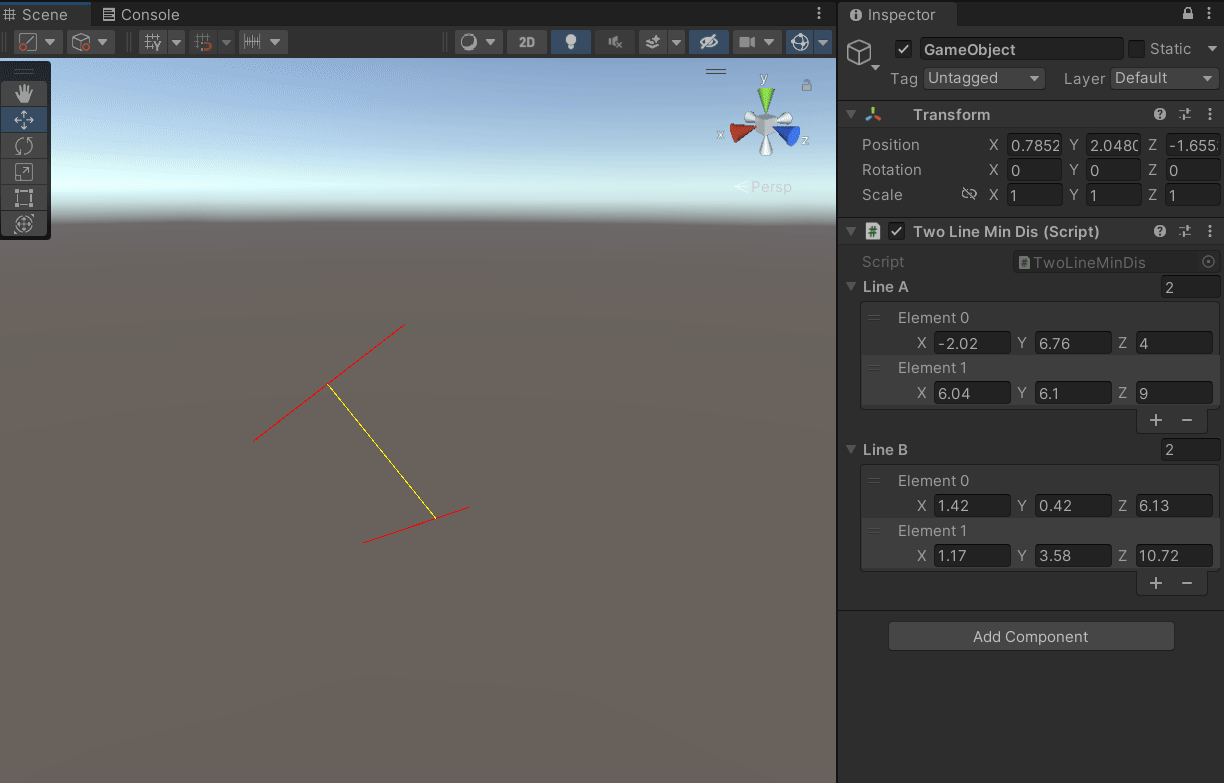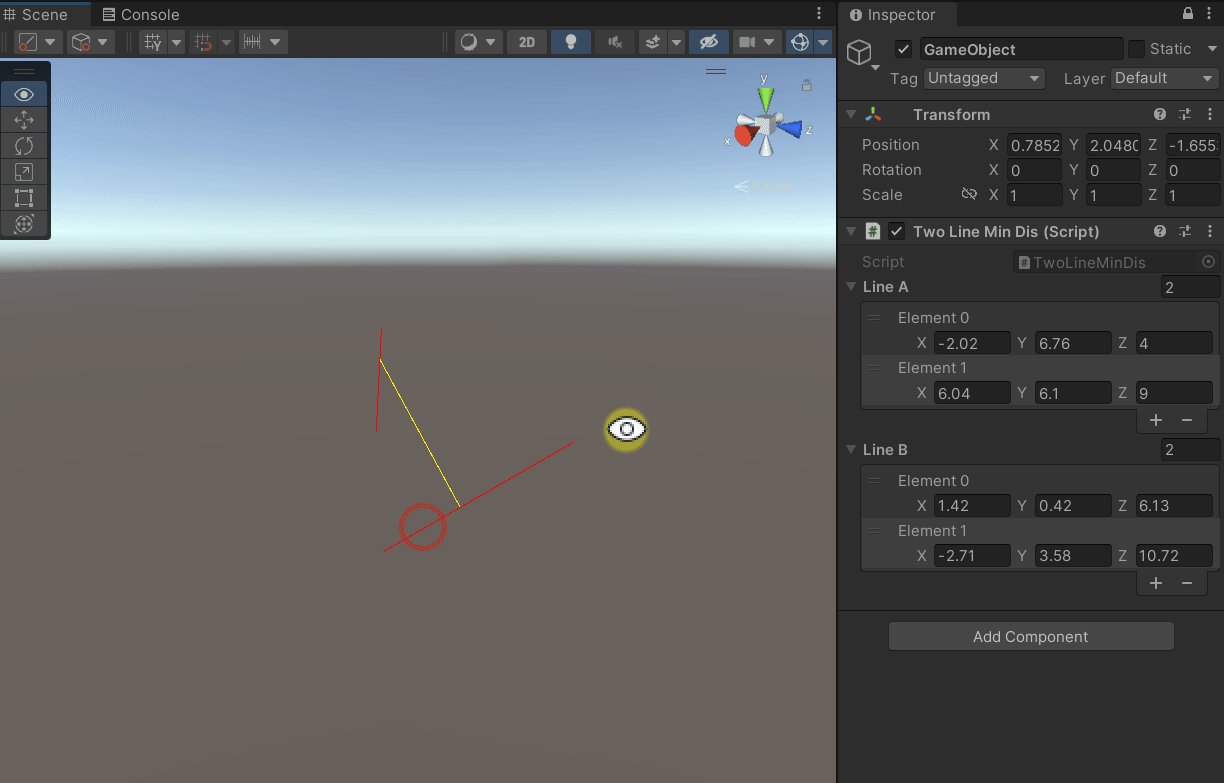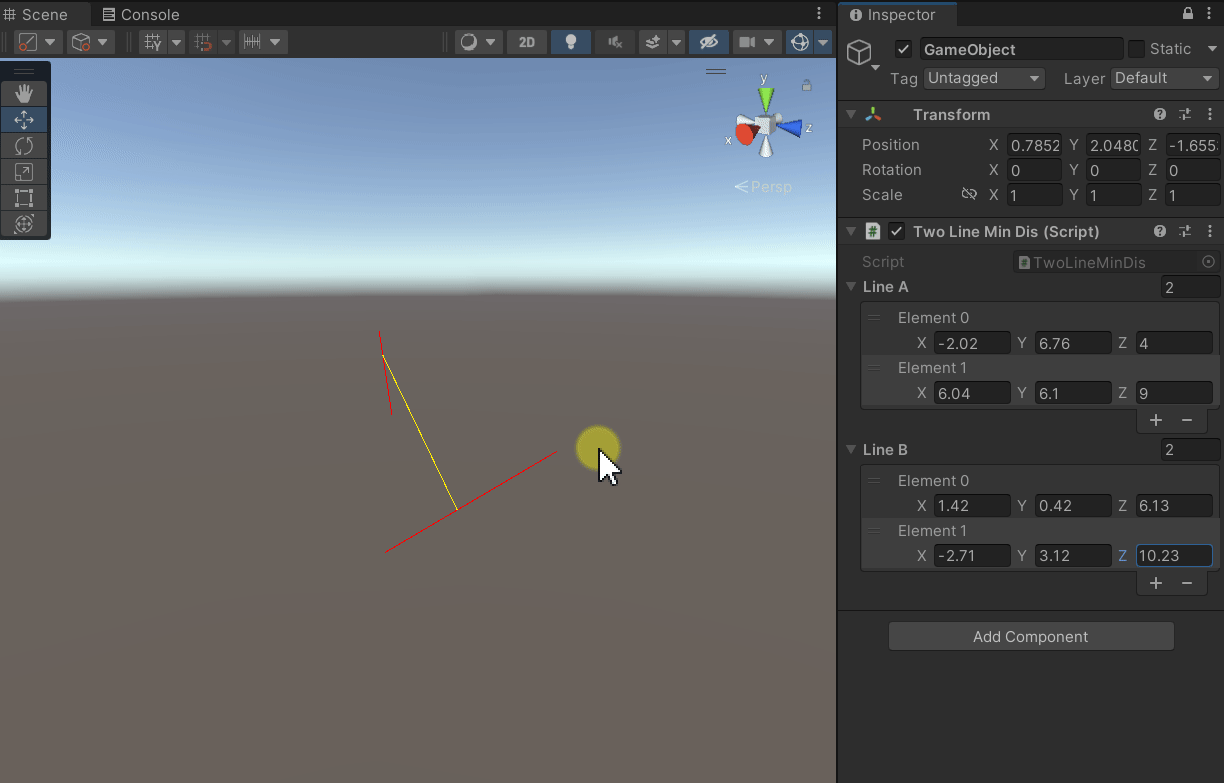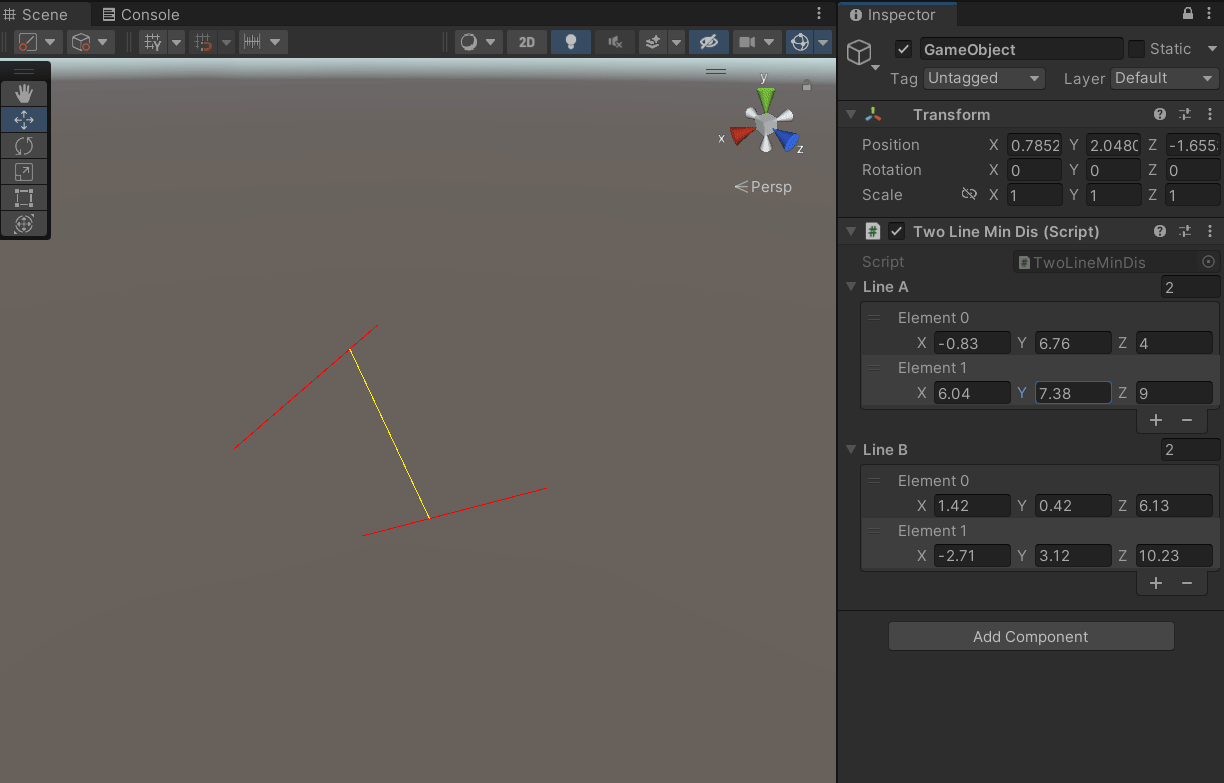
一、问题

已知两条直线 $l_1(x_1,y_1,x_2,y_2)$ 和 $l_2(x_3,y_3,x_4,y_4)$ ，现希望判断 $l_1$ 与 $l_2$ 间是否平行。若平行，计算出两条直线间的平行距离。

二、分析

$\frac{y-y_1}{y_2-y_1} = \frac{x-x_1}{x_2-x_1} \Rightarrow \begin{cases} ax+by+c=0 \\a=-(y_2-y_1) \\b = x_2-x_1 \\c = (y_2-y_1)x_1 - (x_2-x_1) y_1 \\ k = \frac{-a}{b}\end{cases}$

$l_1$ 的直线方程：
$a_1x+b_1y+c_1=0$

$l_2$ 的直线方程：
$a_2x+b_2y+c_2=0$

1、排除 $l_1$ 与 $l_2$ 重合

$l_2$ 的起点 $p_{3}(x_{3},y_{3})$ 和终点 $p_{4}(x_{4},y_{4})$ 不能同时在直线 $l_1$ 上：

    !(p3!=p4 && a1*x3+b1*y3+c1==0 && a1*x4+b1*y4+c1==0)

2、 $l_1$ 与 $l_2$ 都垂直 $x$ 轴

当 $l_1$ 与 $l_2$ 都垂直 $x$ 轴时， $l_1$ 与 $l_2$ 平行：

    b2==0 && b1==0

$l_1$ 与 $l_2$ 的直线方程：
$l_1:a_1x+c_1=0 \quad l_2:a_2x+c_2=0$

$l_1$ 与 $l_2$ 间的距离为：
$|x_2-x_1|= |\frac{c_1}{a_1} - \frac{c_2}{a_2} |$

3、 $l_1$ 与 $l_2$ 都倾斜于 $x$ 轴，且斜率相同

当 $l_1$ 与 $l_2$ 斜率相同时， $l_1$ 与 $l_2$ 平行：

    b2!=0 && b1!=0 && a2/b2==a1/b1

$l_1$ 与 $l_2$ 的直线方程：
$l_1:a_1x+b_1y+c_1=0 \quad l_2:a_2x+b_2y+c_2=0$

$l_2$ 与 $y$ 轴的交点 $p_0$ ：
$(x_0,y_0)=(0,\frac{-c_2}{b_2})$

$p_0$ 到 $l_1$ 距离：
$\frac{|a_1x_0+b_1y_0+c_1|}{\sqrt{a_1^2+b_1^2}} = \frac{|c_1-\frac{b_1c_2}{b_2}|}{\sqrt{a_1^2+b_1^2}}$

三、实现

#include <opencv2/opencv.hpp>
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
using namespace cv;Vec4d g_line1(200, 200, 600, 200), g_line2(200, 400, 600, 400); // 平行的两条线// 判断两条线是否平行，若平行，则求出平行距离
double lines_parellel(const Vec4d l1, const Vec4d l2)
{double x1 = l1[0], y1 = l1[1], x2 = l1[2], y2 = l1[3];                      // 两点式：(y-y1)/(y2-y1)=(x-x1)/(x2-x1)double a1 = -(y2 - y1), b1 = x2 - x1, c1 = (y2 - y1) * x1 - (x2 - x1) * y1; // 一般式：a1x+b1y1+c1=0double x3 = l2[0], y3 = l2[1], x4 = l2[2], y4 = l2[3];                      // 两点式：(y-y3)/(y4-y3)=(x-x3)/(x4-x3)double a2 = -(y4 - y3), b2 = x4 - x3, c2 = (y4 - y3) * x3 - (x4 - x3) * y3; // 一般式：a2x+b2y1+c2=0Point2d p3(x3, y3), p4(x4, y4);double d = 0;if (!(p3 != p4 && a1 * x3 + b1 * y3 + c1 == 0 && a1 * x4 + b1 * y4 + c1 == 0)) // 排除重合的情况{if (b2 == 0 && b1 == 0) // l2，l1垂直x轴{d = abs(c1 / a1 - c2 / a2);}else if (b2 != 0 && b1 != 0 && a2 / b2 == a1 / b1) // l2，l1斜率相同{d = abs(c1 - b1 * c2 / b2) / sqrt(a1 * a1 + b1 * b1);}}return d;
}// 计算垂足的坐标
Point calculate_foot_point(Point2d p, Vec4d l)
{double x0 = p.x, y0 = p.y;double x1 = l[0], y1 = l[1], x2 = l[2], y2 = l[3];Point2d p1(0, 0); // 垂足if (x1 == x2)     // 线与x轴垂直{p1.x = x1;p1.y = y0;}else if (y1 == y2) // 线与x轴水平{p1.x = x0;p1.y = y1;}else // 线与x轴倾斜{int a = -(y2 - y1);int b = x2 - x1;int c = (y2 - y1) * x1 - (x2 - x1) * y1;p1.x = (b * b * x0 - a * b * y0 - a * c) / (a * a + b * b);p1.y = (a * a * y0 - a * b * x0 - b * c) / (a * a + b * b);}return p1;
}// 画虚线
void draw_dotted_line(Mat img, const Point2d p1, const Point2d p2, const Scalar color, const int thickness)
{double n = 15; // 小虚线的长度double w = p2.x - p1.x, h = p2.y - p1.y;double l = sqrtl(w * w + h * h);// 矫正线长度，使线个数为奇数int m = l / n;m = m % 2 ? m : m + 1;n = l / m;circle(img, p1, 1, color, thickness); // 画起点circle(img, p2, 1, color, thickness); // 画终点// 画中间点if (p1.y == p2.y) // 与x轴水平：y = m{double x1 = min(p1.x, p2.x);double x2 = max(p1.x, p2.x);for (double x = x1, n1 = 2 * n; x < x2; x = x + n1)line(img, Point2d(x, p1.y), Point2d(x + n, p1.y), color, thickness);}else if (p1.x == p2.x) // 与x轴垂直, x = m{double y1 = min(p1.y, p2.y);double y2 = max(p1.y, p2.y);for (double y = y1, n1 = 2 * n; y < y2; y = y + n1)line(img, Point2d(p1.x, y), Point2d(p1.x, y + n), color, thickness);}else // 与x轴倾斜，直线方程的两点式：(y-y1)/(y2-y1)=(x-x1)/(x2-x1) -> y = (y2-y1)*(x-x1)/(x2-x1)+y1{double n1 = n * abs(w) / l;double k = h / w;double x1 = min(p1.x, p2.x);double x2 = max(p1.x, p2.x);for (double x = x1, n2 = 2 * n1; x < x2; x = x + n2){Point p3 = Point2d(x, k * (x - p1.x) + p1.y);Point p4 = Point2d(x + n1, k * (x + n1 - p1.x) + p1.y);line(img, p3, p4, color, thickness);}}
}// 画延长线
void draw_extension_line(Mat img, const Vec4d l, Scalar color)
{double x1 = l[0], y1 = l[1], x2 = l[2], y2 = l[3];double a = -(y2 - y1), b = x2 - x1, c = (y2 - y1) * x1 - (x2 - x1) * y1;Point2d p1(0, 0), p2(0, 0);if (b != 0) // 与x轴倾斜{p1 = Point2d(0, -c / b);p2 = Point2d(img.cols, ((-a * img.cols - c) / b));}else // 与x轴垂直{p1 = Point2d(-c / a, 0);p2 = Point2d(-c / a, img.rows);}draw_dotted_line(img, p1, p2, color, 1);
}// 画图
void draw(const Mat img, const Vec4d l1, const Vec4d l2)
{line(img, Point2d(l1[0], l1[1]), Point2d(l1[2], l1[3]), Scalar(0, 255, 0), 2); // 画绿线line(img, Point2d(l2[0], l2[1]), Point2d(l2[2], l2[3]), Scalar(0, 255, 0), 2); // 画绿线double d = lines_parellel(l1, l2);if (d > 0) // 重合{putText(img, "yes d = " + to_string(d), Point2d(10, 25), cv::FONT_HERSHEY_COMPLEX, 0.5, Scalar(0, 255, 0));draw_extension_line(img, l1, Scalar(0, 255, 0));      // 画延长线draw_extension_line(img, l2, Scalar(0, 255, 0));      // 画延长线Point2d p1((l1[2] + l1[0]) / 2, (l1[3] + l1[1]) / 2); // 获取线段的中间点Point p2 = calculate_foot_point(p1, l2);              // 获取垂足draw_dotted_line(img, p1, p2, Scalar(0, 255, 0), 1);  // 画垂线}else // 不重合{putText(img, "no", Point2d(10, 25), cv::FONT_HERSHEY_COMPLEX, 0.5, Scalar(0, 0, 255));}
}// 确定鼠标左键点击在两条直线的那个点上
Vec6d define_area(const Vec4d l1, const Vec4d l2, const Point2d p)
{Vec6d v(-1, 0, 0, 0, 0, 0);double w = 20, h = 20;double x1 = l1[0], y1 = l1[1], x2 = l1[2], y2 = l1[3];double x3 = l2[0], y3 = l2[1], x4 = l2[2], y4 = l2[3];Rect r0(x1 - w, y1 - h, 2 * w, 2 * h);    // l1的起点点Point2d p1((x2 + x1) / 2, (y1 + y2) / 2); // l1的中间点Rect r1(p1.x - w, p1.y - h, 2 * w, 2 * h);Rect r2(x2 - w, y2 - h, 2 * w, 2 * h); // l1的终点Rect r3(x3 - w, y3 - h, 2 * w, 2 * h);    // l2的起点Point2d p2((x3 + x4) / 2, (y3 + y4) / 2); // l2的中间点Rect r4(p2.x - w, p2.y - h, 2 * w, 2 * h);Rect r5(x4 - w, y4 - h, 2 * w, 2 * h); // l2的终点if (r0.contains(p)) // 判断点是否在矩形中{v = Vec6d(0, x1, y1, 0, 0, 0);}else if (r1.contains(p)){v = Vec6d(1, x1, y1, x2, y2, 0);}else if (r2.contains(p)){v = Vec6d(2, x2, y2, 0, 0, 0);}else if (r3.contains(p)){v = Vec6d(3, x3, y3, 0, 0, 0);}else if (r4.contains(p)){v = Vec6d(4, x3, y3, x4, y4, 0);}else if (r5.contains(p)){v = Vec6d(5, x4, y4, 0, 0, 0);}return v;
}// 根据鼠标移动相应的修改直线的起点和终点
void modify_line(Vec4d &l1, Vec4d &l2, const Vec6d area, const double w, const double h)
{if (area[0] == 0){l1[0] = area[1] + w;l1[1] = area[2] + h;}else if (area[0] == 1){l1[0] = area[1] + w;l1[1] = area[2] + h;l1[2] = area[3] + w;l1[3] = area[4] + h;}else if (area[0] == 2){l1[2] = area[1] + w;l1[3] = area[2] + h;}else if (area[0] == 3){l2[0] = area[1] + w;l2[1] = area[2] + h;}else if (area[0] == 4){l2[0] = area[1] + w;l2[1] = area[2] + h;l2[2] = area[3] + w;l2[3] = area[4] + h;}else if (area[0] == 5){l2[2] = area[1] + w;l2[3] = area[2] + h;}
}// 鼠标回调函数
void mouse_callback(int event, int x, int y, int flags, void *param)
{static Point2d p1(0, 0), p2(0, 0);static Vec6d area(-1, 0, 0, 0, 0, 0);switch (event){case cv::EVENT_LBUTTONDOWN: // 鼠标左键点击p1 = Point2d(x, y);area = define_area(g_line1, g_line2, p1); // 确定鼠标所要移动的区域break;case cv::EVENT_MOUSEMOVE: // 鼠标移动if (area[0] > -1)     // 移动直线{p2 = Point2d(x, y);double w = p2.x - p1.x, h = p2.y - p1.y;modify_line(g_line1, g_line2, area, w, h); // 根据鼠标移动相应的修改直线的起点和终点}break;case cv::EVENT_LBUTTONUP: // 鼠标左键释放p1 = Point2d(0, 0);p2 = Point2d(0, 0);area = Vec6d(-1, 0, 0, 0, 0, 0);break;default:break;}
}// 主函数
int main()
{string window_name = "image";namedWindow(window_name, WINDOW_AUTOSIZE);int w = 800, h = 600;Mat image_original = Mat(h, w, CV_8UC3, Scalar(255, 255, 255));cv::setMouseCallback(window_name, mouse_callback); // 调用鼠标回调函数while (true){Mat img = image_original.clone(); // 拷贝空白图片，方便重复画图draw(img, g_line1, g_line2);      // 画图imshow(window_name, img);char c = waitKey(3);if (c == '1') // l1,l2与x轴平行{g_line1 = Vec4d(200, 200, 600, 200);g_line2 = Vec4d(200, 400, 600, 400);}else if (c == '2') // l1,l2与x轴垂直{g_line1 = Vec4d(300, 200, 300, 400);g_line2 = Vec4d(500, 200, 500, 400);}else if (c == '3') // l1,l2与x轴右倾斜{g_line1 = Vec4d(200, 450, 600, 150);g_line2 = Vec4d(200, 500, 600, 200);}else if (c == '4') // l1,l2与x轴左倾斜{g_line1 = Vec4d(100, 100, 500, 500);g_line2 = Vec4d(100, 150, 500, 550);}else if (c > 0 && (c < '1' || c > '4')) // 退出循环{break;}}return 0;
}

操作方法：
鼠标点击两条直线的起点或终点并按住移动，由此可以修改直线。鼠标点击两条直线的中间点并按住移动，由此可以平移直线。
键盘按住1、2、3或4可选择对应的模式，画出不同角度下两条直线平行的情况。键盘按其它的键会退出程序。

两条直线不平行时：