最近在建立气凝胶的有限元模型中需要计算每两根纤维（线段）之间的距离，最初参考的两篇文章确实提供了关于一些数值方法的计算思路（文章1 && 文章2），但忽略了线段距离问题的理论推导，导致无法用参数 $t$ 正确描述两目标线段！所求得的结果错误。本文从理论推导和程序实现两方面来说明求空间线段之间距离的方法。

理论推导

空间直线的参数方程

如果一个非零向量平行于一条已知直线，这个向量就叫做这条直线的方向向量
由于过空间一点可作而且只能作一条直线平行于一已知直线，所以当直线$L$上一点$M_0\left(x_0,y_0,z_0\right)$和它的一方向向量$\mathbf{s}=\left(m,n,p\right)$为已知时，直线$L$的位置就完全确定了。下面我们来建立这直线的方程。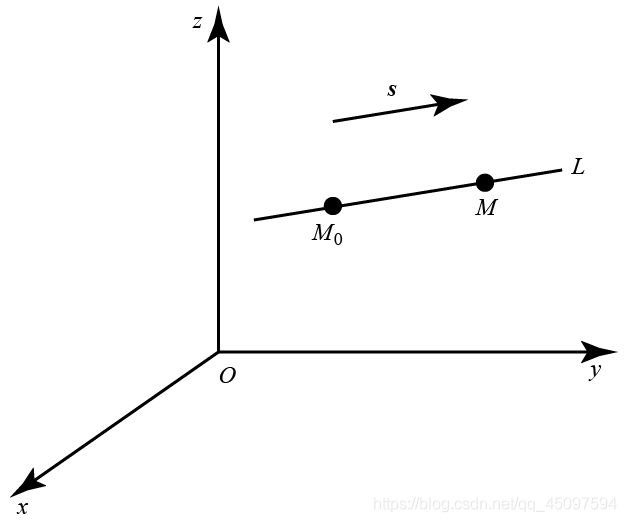
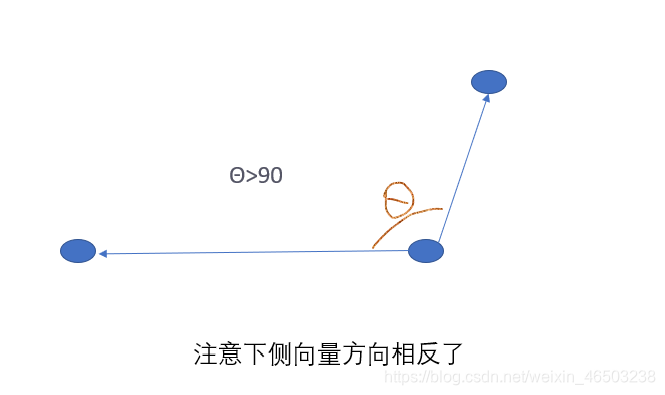
设点$M\left(x,y,z\right)$是直线$L$上的任意一点，那么向量$\overrightarrow{M_{0}M}$与$L$的方向向量$\mathbf{s}$平行（如上图所示）。所以两向量的对应坐标成比例，由于$\overrightarrow{M_{0}M}=\left(x-x_0,y-y_0,z-z_0\right)，\mathbf{s}=\left(m,n,p\right)$，从而有
$$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}$$

反过来，如果点$M$不在直线上，那么由于$\overrightarrow{M_{0}M}$与$\mathbf{s}$不平行，这两向量的对应坐标就不成比例。因此上式方程组就是直线L的方程，叫做直线的对称式方程或点向式方程。

由直线的对称式方程容易导出直线的参数方程。如设

$$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t$$

那么
$$\{\begin{array}{ll}\begin{array}{c}x=x_0+mt\\ y=y_0+nt\\ z=z_0+pt\end{array}& t\in \left(-\infty ,+\infty \right)\end{array}$$

上式就是直线的参数方程。

线段的参数方程

设$A\left(x_1,y_1,z_1\right)$和$B\left(x_2,y_2,z_2\right)$为线段$L$的两端点，则线段$L$的方向向量$\mathbf{s}=\left(x_2-x_1,y_2-y_1,z_2-z_1\right)$，点$M\left(x,y,z\right)$是线段$L$上的任意一点，则线段的参数形式为

$$\{\begin{array}{ll}\begin{array}{c}x=x_1+\left(x_2-x_1\right)t\\ y=y_1+\left(y_2-y_1\right)t\\ z=z_1+\left(z_2-z_1\right)t\end{array}& t\in \left[0,1\right]\end{array}$$

线段之间距离的数值解法

线段之间距离的数值解法是将参数 $t$ 在区间 $[0,1]$ 上均匀离散，每个 $t$ 的取值，对应线段上的一个点。将求线段间的距离转化为求两线段上点的距离集合的最小值。（两线段上点的距离集合是指 $a$ 线段的每个离散点与 $b$ 线段上的所有离散点之间的距离，若设 $a$ 线段上的离散点个数为 $m$ ， $b$ 线段上的离散点个数为 $n$ ，则两线段上点的距离集合元素的个数为：$m\times n$）。该方法所求出的线段之间的距离为近似值，所求结果的精度取决于线段上离散点的数量。

程序实现

double LinesDistance_another_method(double *line1,double *line2)
{int i,j,m,n;double *t1,*t2,*x1,*y1,*z1,*x2,*y2,*z2,**juli,min_value;double DirectionVector_m1,DirectionVector_n1,DirectionVector_p1;double DirectionVector_m2,DirectionVector_n2,DirectionVector_p2;t1 = new double [11];t2 = new double [11];x1 = new double [11];x2 = new double [11];y1 = new double [11];y2 = new double [11];z1 = new double [11];z2 = new double [11];DirectionVector_m1=line1[3]-line1[0];DirectionVector_n1=line1[4]-line1[1];DirectionVector_p1=line1[5]-line1[2];// 	printf("line1: \n");// 	printf("x1=%lf,x2=%lf\n",line1[0],line1[3]);// 	printf("x2-x1=%lf\n",DirectionVector_m1);for (i = 0;i < 11;i++){t1[i]=0.1*i;/*		printf("t1[%d]=%lf\n",i,t1[i]);*/}for (i = 0;i < 11;i++){x1[i]=line1[0]+DirectionVector_m1*t1[i];y1[i]=line1[1]+DirectionVector_n1*t1[i];z1[i]=line1[2]+DirectionVector_p1*t1[i];/*		printf("x1[%d]=%lf\n",i,x1[i]);*/}DirectionVector_m2=line2[3]-line2[0];DirectionVector_n2=line2[4]-line2[1];DirectionVector_p2=line2[5]-line2[2];// 	printf("line1: \n");// 	printf("x1=%lf,x2=%lf\n",line2[0],line2[3]);// 	printf("x2-x1=%lf\n",DirectionVector_m2);for (i = 0;i < 11;i++){t2[i]=0.1*i;/*		printf("t2[%d]=%lf\n",i,t2[i]);*/}for (i = 0;i < 11;i++){x2[i]=line2[0]+DirectionVector_m2*t2[i];y2[i]=line2[1]+DirectionVector_n2*t2[i];z2[i]=line2[2]+DirectionVector_p2*t2[i];/*		printf("x2[%d]=%lf\n",i,x2[i]);*/}n=11;//n=length(t1);m=11;//m=length(t2);juli = new2DDouble(n,m);for (i = 0;i < n;i++){for (j = 0;j < m;j++){juli[i][j]=sqrt(pow((x2[j]-x1[i]),2)+pow((y2[j]-y1[i]),2)+pow((z2[j]-z1[i]),2));}}min_value=juli[0][0];for (i = 0;i < n;i++){for (j = 0;j < m;j++){if (min_value>juli[i][j]){min_value=juli[i][j];}}}freeDoubleArray2(juli,n);juli = NULL;delete [] t1;t1 = NULL;delete [] t2;t2 = NULL;delete [] x1;x1 = NULL;delete [] x2;x2 = NULL;delete [] y1;y1 = NULL;delete [] y2;y2 = NULL;delete [] z1;z1 = NULL;delete [] z2;z2 = NULL;return min_value;
}

double **new2DDouble(int col,int lin)
{double **newArray;newArray = new double *[col];for(int i=0;i<col;i++){  newArray[i]=new double[lin];}for(int i=0;i<col;i++){  for(int j=0;j<lin;j++){newArray[i][j]=0.0;}}return newArray;
}

void freeDoubleArray2(double **Array,int NIFF0)
{int i;for(i=0;i<NIFF0;i++){delete [] Array[i];				}delete [] Array;Array = NULL;
}

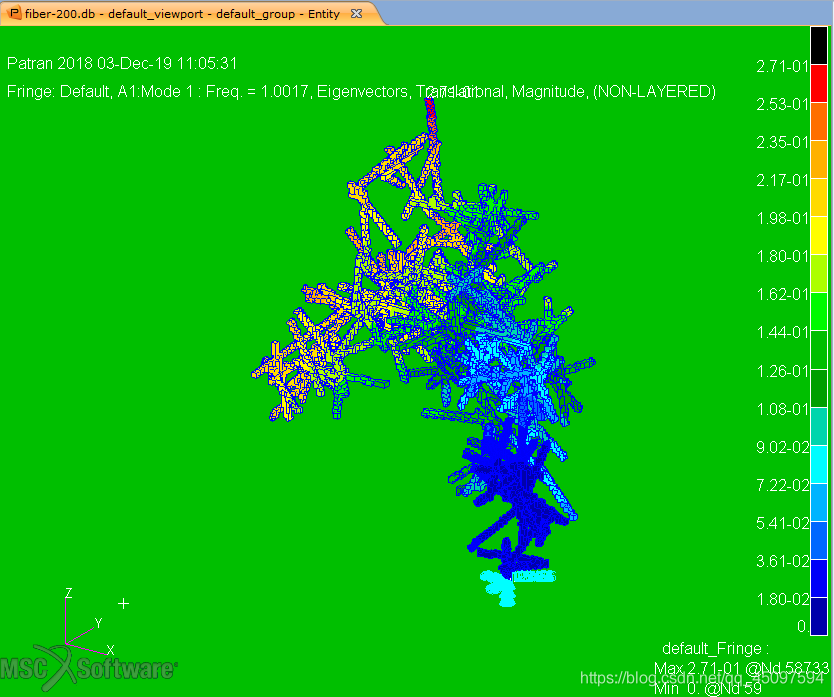
方法的验证

在纤维组成的气凝胶模型中，为了使纤维之间能够连接到一起，就需要严格控制纤维之间的距离。所以引用这里的求线段之间距离的方法，来筛选出满足距离要求的纤维。那么若纤维之间不能很好的相连，则说明距离求解有误。下图为气凝胶模型的一小部分结构，对其进行有限元的模态分析来检验模型的连接状态。由其云图结果可知该模型已经连接成为一整体，该方法有效！