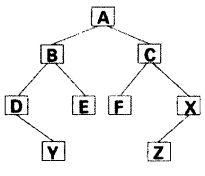
一、图的基本概念
图是由顶点集合及顶点间的关系集合组成的一种数据结构。vertex, edge
图G的定义是: G =(V,E)
其中,
V = {x|x∈某个数据元素集合}
E ={ (x,y)|x,y∈V} (无向图) 或
E = { <x, y>|x,y∈V并且Path(x, y)} (有向图)
其中,(x,y)表示从 x到 y的一条双向通路,即(x,y)是无方向的;
Path(x,y)表示从 x到 y的一条单向通路,即Path(x,y)是有方向的。
图的基本术语:
(1)顶点和边:
(2)有向图和无向图:
(3)完全图:
(4)邻接顶点:
(5)顶点的度:
(6)路径:
(7)权:
(8)路径长度:
(9)子图:
(10)连通图(无向图)和强连通图(有向图) :
(11)生成树(无向图) :
(12)简单路径和回路:
二、图的存储结构
图的存储结构主要有邻接矩阵和邻接表两种。
2.1、图的邻接矩阵存储结构
1)无向图的邻接矩阵一定是对称矩阵: 其中V表示了图的顶点集合,A表示了图的邻接矩阵

2)有向图的邻接矩阵一般是非对称矩阵:其中V表示了图的顶点集合,A表示了图的邻接矩阵

带权图及其邻接矩阵 :其中V表示了图的顶点集合,A表示了图的邻接矩阵。
对于带权图:
邻接矩阵第i行中所有0<aij<∞的元素个数等于第i个顶点的出度。
邻接矩阵第j列中所有0<aij<∞的元素个数等于第j个顶点的入度。

2.2、图的邻接表存储结构