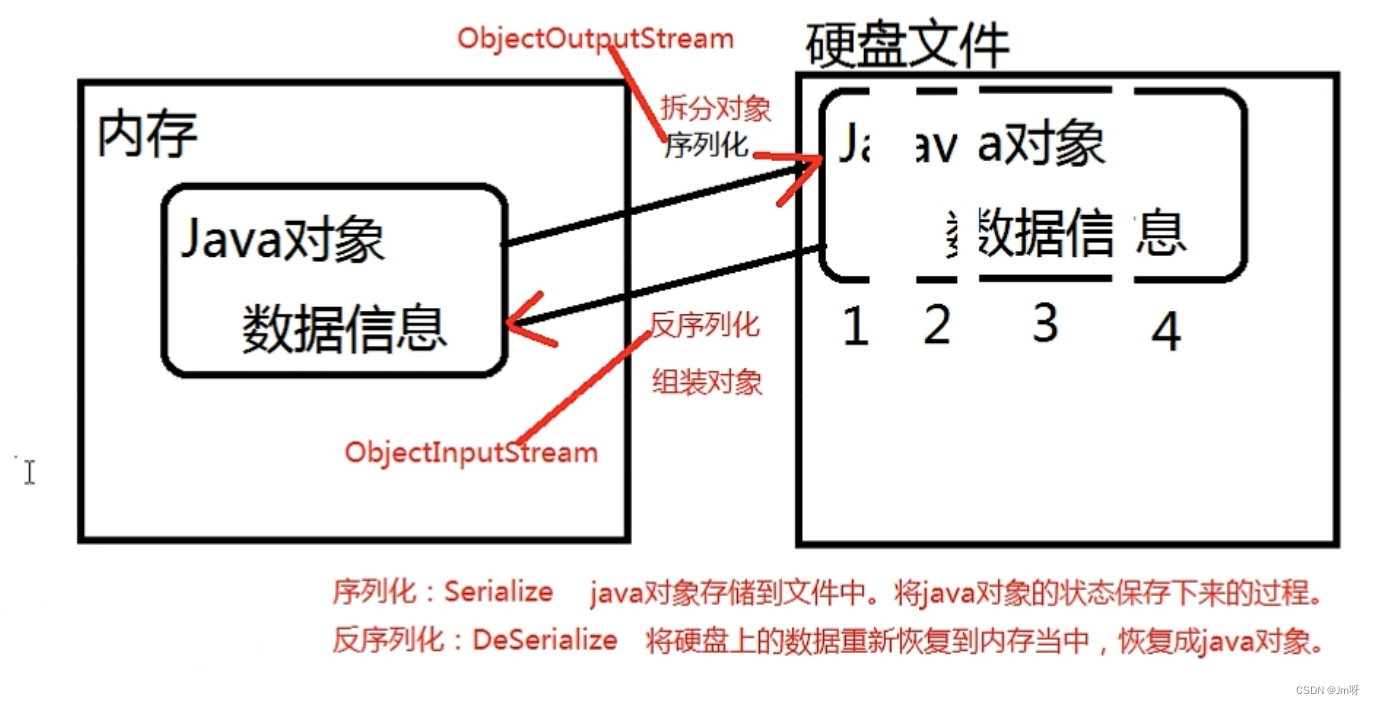
一、介绍
使用短信验证登录也是现在实际项目中普遍使用的一种登录,
二、实际的操作流程
1.用户在前端页面输入手机号码之后,点击发送验证码
2.前端将手机号传给后端
3.后端生成一个6为的随机数通过短信发送给用户,之后将手机号设为key,验证码设为value存入redis缓存中,最后将短信发送是否成功返回给前端
4.当用户收到短信后,输入验证码,点击登录
5.前端将手机号和验证码发送和后端
6.后端从缓存中获取key和value,验证输入的验证码是否正确,在将结果返回给前端
7.短信验证结束
三、项目实现
1.去阿里云官网购买短信服务,阿里云官网https://www.aliyun.com/
2.添加签名和模板
点击左侧国内消息,先进行审核,必须是审核通过状态

3.签名管理中添加签名,签名就是发送短信时的公司名
4.模板管理添加模板,内容就是发送短信的内容
5.获取阿里云私钥
点击左侧概览,在后侧看见

6.获取发送短信的代码