题目

假设向量y=[7613.51  7850.91  8381.86  9142.81 10813.6 8631.43 8124.94 9429.79 10230.81 10163.61 9737.56 8561.06 7781.82 7110.97];

x1=[7666 7704 8148 8571 8679 7704 6471 5870 5289 3815 3335 2927 2758 2591];

x2=[16.22 16.85 17.93 17.28 17.23 17 19 18.22 16.3 13.37 11.62 10.36 9.83 9.25];

是一个表格中三个列向量。

建立的基本模是：

y=Ax1^2+Bx2^2+Cx1+Dx2+Ex1*x2;

利用regress函数求解各个系数的估计值。

分析

regress命令——用于一元及多元线性回归，本质上是最小二乘法。在Matlab中，输入help regress ，会弹出和regress的相关信息：

调用格式：

B = regress(Y,X)
[B,BINT] = regress(Y,X)
[B,BINT,R] = regress(Y,X)
[B,BINT,R,RINT] = regress(Y,X)
B,BINT,R,RINT,STATS] = regress(Y,X)
[...] = regress(Y,X,ALPHA)

参数解释：

B：回归系数，是个向量（“the vector B of regression coefficients in the  linear model Y = X*B”）。
BINT：回归系数的区间估计（“a matrix BINT of 95% confidence intervals for B”）。
R：残差（ “a vector R of residuals”）。
RINT：置信区间（“a matrix RINT of intervals that can be used to diagnose outliers”）。
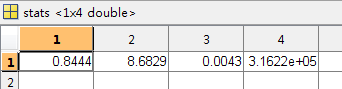
STATS：用于检验回归模型的统计量。有4个数值：判定系数R^2，F统计量观测值，检验的p的值，误差方差的估计。
ALPHA：显著性水平（缺少时为默认值0.05）。

解题

 

>> y=[7613.51  7850.91  8381.86  9142.81 10813.6 8631.43 8124.94 9429.79 10230.81 10163.61 9737.56 8561.06 7781.82 7110.97]'; 
>> x1=[7666 7704 8148 8571 8679 7704 6471 5870 5289 3815 3335 2927 2758 2591]';  
>> x2=[16.22 16.85 17.93 17.28 17.23 17 19 18.22 16.3 13.37 11.62 10.36 9.83 9.25]'; 
>> X=[ones(size(y)) x1.^2 x2.^2 x1 x2 x1.*x2];   %size(y)求y的长度，ones全1阵
>> [b,bint,r,rint,stats] = regress(y,X); 
>> scatter3(x1,x2,y,'filled')

散列图为：

     

                   

                                                

 

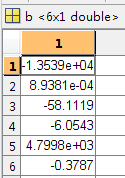
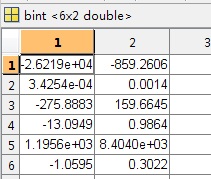
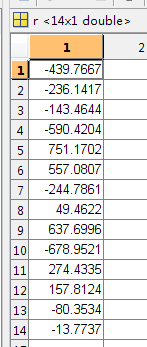
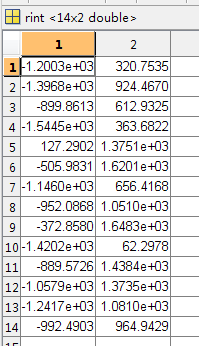
    b为对应的参数 b(1)为F(最后那个常数项) ，b(2)为A（第一个参数），b(3)为B，b(4)为C，b(4)为D，b(5)为E。bint为b的95%置信区间。

   stats的第三个参数为F检测的P值，p值很小（P<0.001）,说明拟合模型有效。（这里的分析技巧，以后有时间的话，会专门总结。）

附加

对散点数据进行拟合

>>  hold on
>>  x1fit = min(x1):100:max(x1);
>>  x2fit = min(x2):1:max(x2);
>> [X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
>> YFIT=b(1)+b(2)*X1FIT.^2+b(3)*X2FIT.^2+b(4)*X1FIT+b(5)*X2FIT+b(6)*X1FIT.*X2FIT; 
>>  mesh(X1FIT,X2FIT,YFIT)
>> view(10,10)
>> xlabel('x1')
>>  ylabel('x2') 
>> zlabel('y') 

截图为

参考文献：regress命令篇