matlab中多元线性回归regress函数精确剖析(附实例代码)
目录
前言
一、何为regress?
二、regress函数中的参数
三、实例分析
总结
前言
regress函数功能十分强大,它可以用来做多元线性回归分析,它不仅能得出线性回归函数中各个系数,还会返回一系列有意义的统计参数,有助于我们对回归函数的分析。本次介绍regress函数的基本功能然后配置以具体实例展示regress函数如何使用。
提示:以下是本篇文章正文内容,均为作者本人原创,写文章实属不易,希望各位在转载时附上本文链接。
一、何为regress?
regress函数用来做多元线性回归(Multiple linear regression)。简单点说,就比如说现在给了几组关于y、x1、x2数据,他们之间满足某种关系例如,我们就可以用这个函数借助已知数据求出a、b、c、d的值。
二、regress函数中的参数
regress函数的使用格式如下:
[b,bint,r,rint,stats] = regress(y,X,alpha);b------ returns a vector b of coefficient estimates for a multiple linear regression of the responses in vector y on the predictors in matrix x. The matrix x must include a column of ones. b是一个列向量返回的是在x和y这组数据下得到的多元线性回归的系数估计向量b,矩阵x必须包含一列1。至于x为什么需要包含一列1见下面对x的分析。
bint------returns a matrix bint of 95% confidence intervals for the coefficient estimates. 返回系数估计值的95%置信区间的矩阵绑定。bint是一个多行两列的矩阵,返回系数估计值的95%置信区间。对于置信区间的理解简单点说就是可信度,学过概率论就会明白何为置信区间。bint的每一行有两个值,可看成一个区间的上下界,它的每一行这个区间就是参数b中每一行的那个参数的95%的置信区间。
r------returns an additional vector r of residuals. r是residual的简写,就是残差的意思。r返回一个列向量,r中的每一个值就是真实的数据y减去预测的y值得到的,称之为残差。
rint------returns a matrix rint of intervals that can be used to diagnose outliers. 返回的也是一个多行两列的矩阵,它的理解可同bint,只不过此时判断的是r的可信区间。
stats------returns a vector stats that contains the statistic, the F-statistic and its p-value, and an estimate of the error variance. stats翻译成中文就是‘统计’的意思,返回的是一个包含各种统计量的行向量,包含
统计量、F统计量观测值及检验的p值和误差方差估计值的一个行向量。
越接近1,回归方程越显著;
时拒绝
,F越大,回归方程越显著;
时拒绝
。此处又涉及到概率论的假设检验的知识,学过概率论就会有所了解。这里我们可以只重点关注
的值,也就是相关系数的值,它可以帮助我们判断回归方程的优劣。
y------是一个列向量,是已知数据。
x------是一个矩阵,它的第一列全为1,有没有全为1的这一列决定回归方程是否含有拟合的常数参数,也就是中的d这个参数是否有被拟合出来。在程序中对应于全1的那一列一般表示为:ones(size(y)) ,其中x1和x2是多元线性回归方程中的自变量,是已知数据。如下:
x=[ones(size(y)),x1,x2];alpha------显著性水平,缺省时默认为0.05。
三、实例分析
这里我们拟合一个方程,Q,K,L是已知数据,K,L视为自变量,Q视为因变量,需要求得是a,
和
的值。显然它不是一个线性方程,那么我们就对它两边同时取对数,得到:
,此时将LnQ看成一个整体,作为因变量,LnK和LnL看成两个整体,作为自变量,那么就变成线性方程了。
实例用到的程序如下:
Q=[1.05 1.18 1.29 1.30 1.30 1.42 1.50 1.52 1.46 1.60 1.69 1.81 1.93 1.95 2.01 2.00 2.09 1.96 2.20 2.12 2.16 2.08 2.24 2.56 2.34 2.45 2.58]';
y=log(Q);
K=[1.04 1.06 1.16 1.22 1.27 1.37 1.44 1.53 1.57 2.05 2.51 2.63 2.74 2.82 3.24 3.24 3.61 4.10 4.36 4.77 4.75 4.54 4.54 4.58 4.58 4.58 4.54]';
x1=log(K);
L=[1.05 1.08 1.18 1.22 1.17 1.30 1.39 1.47 1.31 1.43 1.58 1.59 1.66 1.68 1.65 1.62 1.86 1.93 1.96 1.95 1.90 1.58 1.67 1.82 1.60 1.61 1.64]';
x2=log(L);
x=[ones(size(y)),x1,x2];
[b,bint,r,rint,stats] = regress(y,x);
a=exp(b(1));alpha=b(2);beta=b(3);
R=stats(1);
% % %Plot the data and the model.% % %
scatter3(x1,x2,y,'filled'); %scatter3函数用于画三维散点图
hold on;
x1fit = min(x1):0.05:max(x1);
x2fit = min(x2):0.05:max(x2);
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);%meshgrid用于画曲面图
YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT ;
mesh(X1FIT,X2FIT,YFIT);
title("LnQ=Lna+\alphaLnK+\betaLnL");
xlabel('LnK');
ylabel('LnL');
zlabel('LnQ');
view(50,10);
hold off;
% % %Plot the data and the model.% % %
figure(2);
x1=exp(x1);
x2=exp(x2);
y=exp(y);
scatter3(x1,x2,y,'filled');
hold on;
x1fit = min(x1):0.05:max(x1);
x2fit = min(x2):0.05:max(x2);
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
YFIT = a*(X1FIT.^alpha).*(X2FIT.^beta);
mesh(X1FIT,X2FIT,YFIT);
title("Q=aK^{\alpha}L^{\beta}");
xlabel('K');
ylabel('L');
zlabel('Q');
view(50,20);%view函数用于调整我们看三维图形的视角
hold off;运行完程序regress函数就会返回给我们各种参数的值。例如向量b:
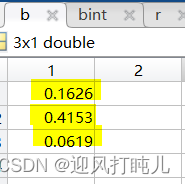
这三个值分别是Lna、和
的值。
再如矩阵bint:

每一行的两个数就是前面b向量的置信区间,也就是上面三行分别为Lna、和
的95%的置信区间。
再如列向量r:
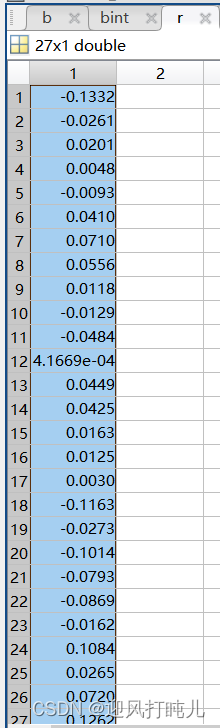
每一行的数值等于真实的数据LnQ减去拟合的数据LnQ,称之为残差。
再如矩阵rint:
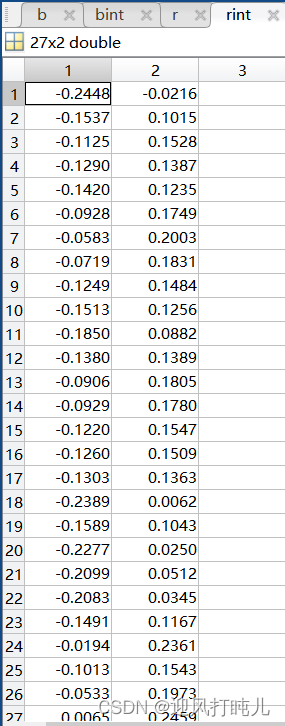
每一行的两个数视为一个区间,理解为与其相对应的残差的可信区间。
再如行向量stats:

只需关注的值即可,越接近于1越好。
运行完程序还会得到两个图,帮助我们直观的感受到拟合的效果,两个图本质上是一样的,区别一个取了对数,一个没取对数,具体情况见下面图当中的title。
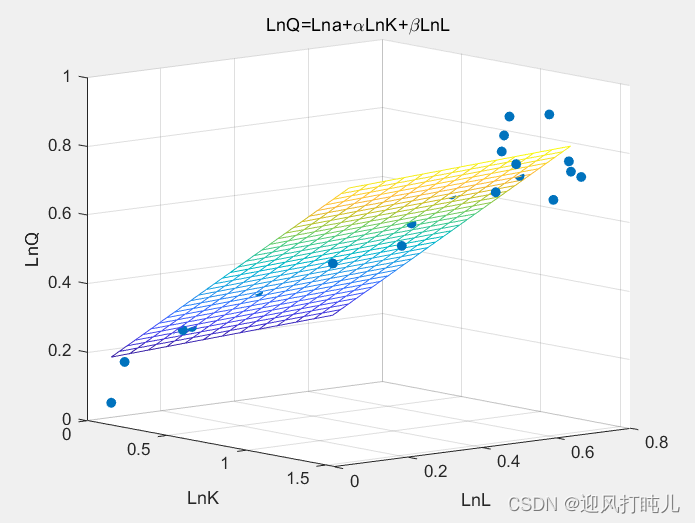
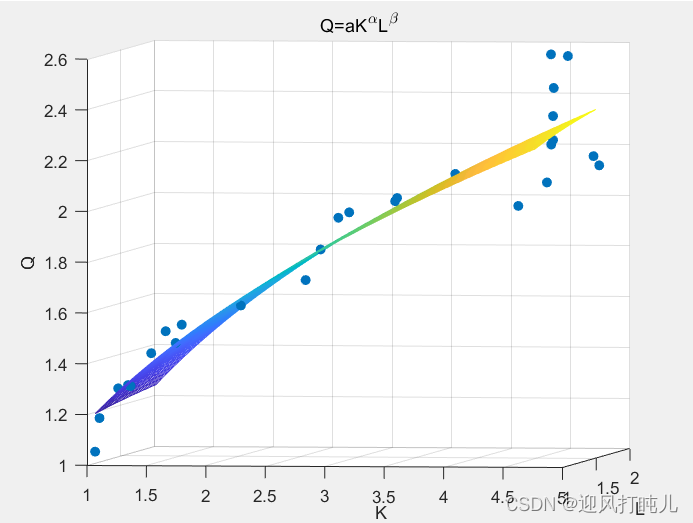
上面的实例拟合的均只含有自变量的一次项,那如果含有二次项在程序中应该怎么写了,例如,只需修改X即可,具体参考下面:
x=[ones(size(y)),x1.^2,x2.^2,x1.*x2,x1,x2];
[b,bint,r,rint,stats] = regress(y,x);总结
以上就是本次要分享的内容,本文详细介绍了regress函数的使用,学会了就赶紧动起手来实操吧。








![[Yar] yar安装与使用过程中遇到问题总结](https://img-blog.csdn.net/20181010155329447?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2ppYWhhb2FuZ2xl/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)