OpenCV中的「SVM分类器」：基本原理、函数解析和示例代码

文章目录

- 1. 引言
- 2. 基本原理
- 3. 函数解析
- - 创建模型
  - 设置模型类型
  - 设置参数C
  - 设置核函数
  - 设置迭代算法的终止标准
  - 训练SVM模型
  - 预测结果
  - 误差计算
  - 保存SVM模型
  - 从文件中加载SVM
- 4. 示例代码
- - 官方示例（python）
  - 推理阶段（C++版本）
- 5. 小结

1. 引言

opencv中集成了基于libsvm¹实现的SVM接口，便于直接进行视觉分类任务。

对于数据处理和可视化需求来说，可以用python接口opencv的SVM更加直观方便。

训练完模型后，将SVM模型保存为xml，可以在实时性应用中通过C++接口调用参数文件，进行实时推断。

在非均衡样本的分类训练中，用opencv中SVM默认的train函数，容易导致分类器偏向数量多的类别，这时可以采用trainAuto函数进行平衡。

如果你对SVM的原理有一定了解，可以直接跳转第3、4小节。

2. 基本原理

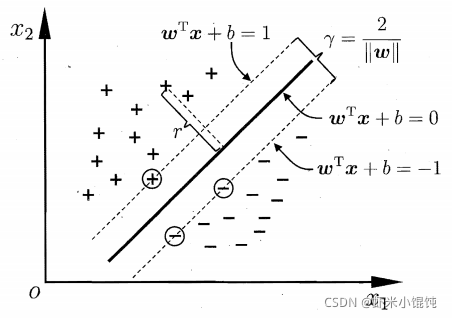
在这里插入图片描述

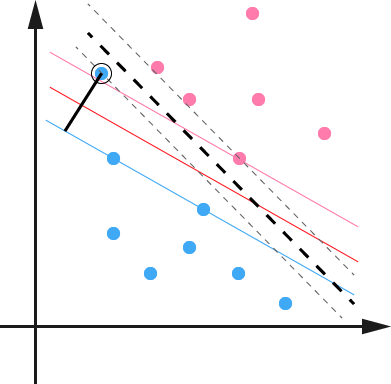
SVM旨在找到一个划分超平面，使得划分后的分类结果是最鲁棒的，对未见过的样本泛化性最好²。

在样本空间中，划分超平面可以用这个方程进行描述： $\boldsymbol{w}^T\boldsymbol{x}+b=0$ ，其中 $\boldsymbol{w}=(w_1;w_2;...;w_d)$ 为法向量，决定超平面的方向，b为位移项，决定超平面与原点之间的距离。

对于线性可分的样本空间，需要找到具有最大间隔（maximum margin）的划分超平面，即找到能使下式最大化的参数 $\boldsymbol{w}$ 和b²：
$\min_{w,b}{\frac{1}{2}||\boldsymbol{w}||^2}$ s.t. $y_i(\boldsymbol{w}^T\boldsymbol{x_i}+b)≥1,i=1,2,...,m$

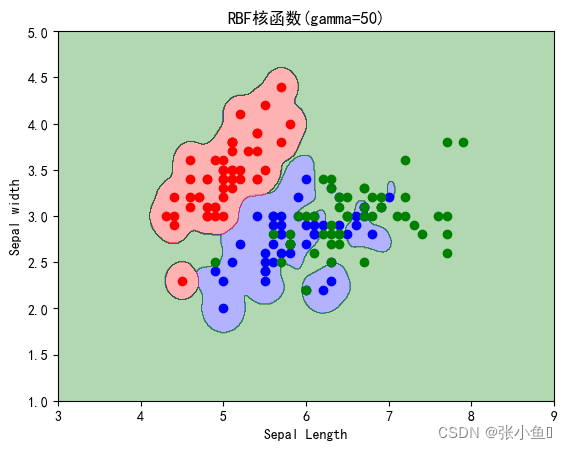
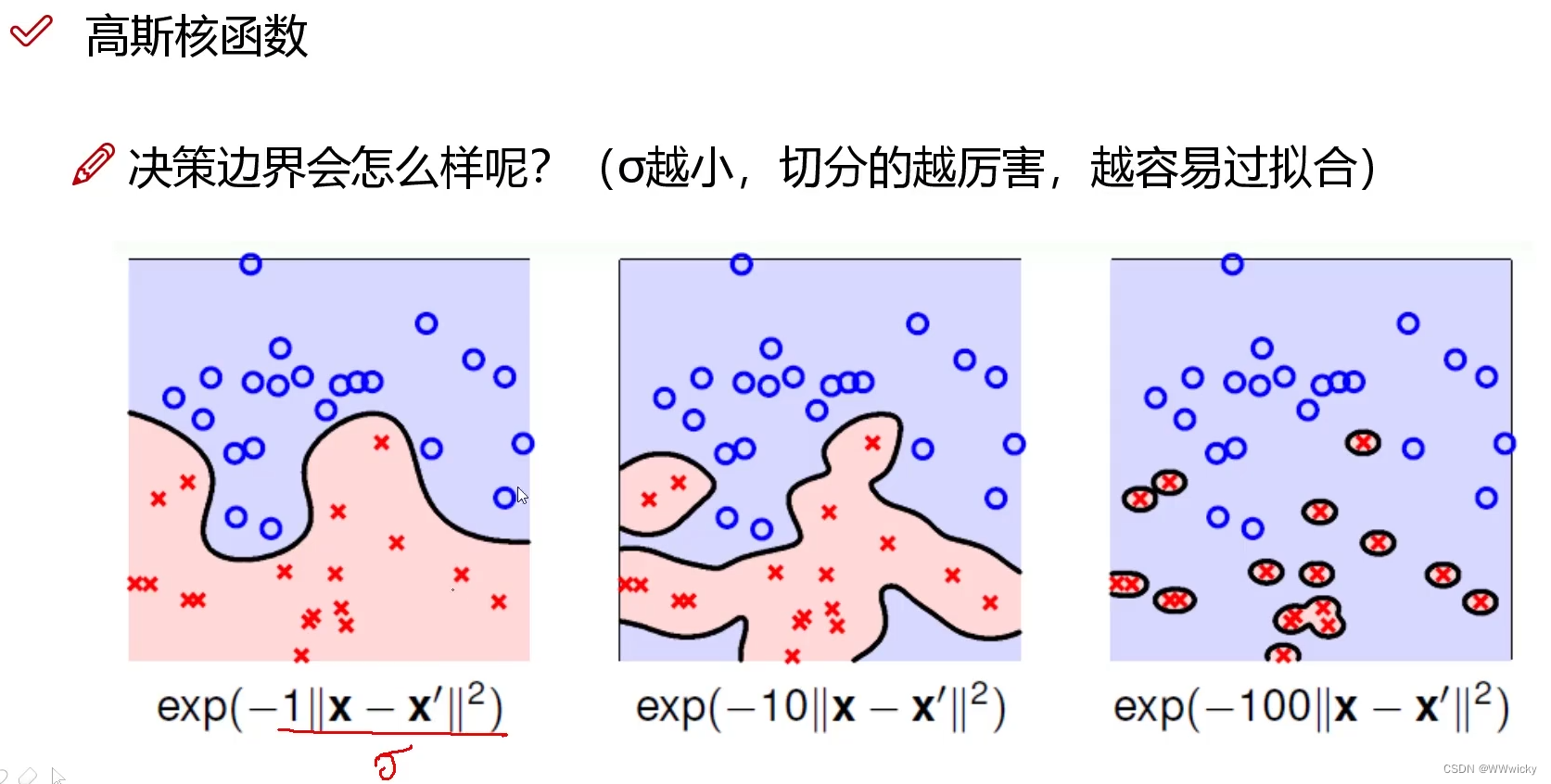
对于线性不可分的样本空间，可以将样本从原始空间映射到另一个高维特征空间，从而使样本在这个特征空间内线性可分。由于特征空间的维数可能很高，难以计算，所以通过引入核函数，可以将高维特征空间中的内积（dot product）转化为低维特征空间中的通过核函数计算的结果。

常用核函数²：
在这里插入图片描述

为了减少过拟合，引入软间隔（soft margin）概念，允许支持向量机在一些样本上出错：
$y_i(\boldsymbol{w}^T\boldsymbol{x_i}+b)≥1$

用参数C来约束分类出错的样本，松弛变量 $ξ_i$ 表示训练样本距离对应的正确决策边界的距离，对于分类正确的样本距离即为0³，所以实际累加的是出错样本的距离。

在这里插入图片描述

优化问题调整为：
$min_{\boldsymbol{w},b_0}{||\boldsymbol{w}||^2+C\sum_i{ξ_i}}$

s.t. $y_i(\boldsymbol{w}^T\boldsymbol{x_i}+b_0)≥1-ξ_i,且ξ_i≥0 ∀i$

3. 函数解析

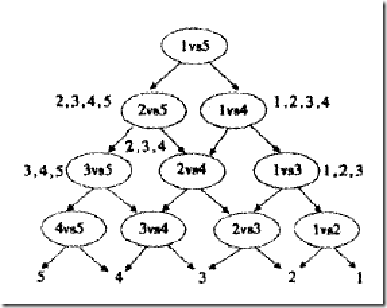
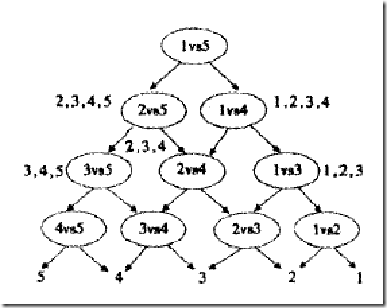
SVM类在opencv中的继承关系如图所示⁴：

在这里插入图片描述
SVM继承自StatModel和Algorithm类。

在opencv中使用SVM的一般流程如下：

创建模型

C++：

static Ptr<SVM> cv::ml::SVM::create()

Python：

cv.ml.SVM_create() -> retval

设置模型类型

C++：

enum  Types {C_SVC =100,//C-支持向量分类。n级分类（n≥ 2) 允许使用异常值的惩罚乘数 C 不完全地分离类。NU_SVC =101,//ν-支持向量分类。n级分类，可能有不完美的分离。参数ν用于代替C，参数ν在0-1范围内，值越大，决策边界越平滑。ONE_CLASS =102,//分布估计，所有的训练数据都来自同一个类，SVM 构建了一个边界，将类与特征空间的其余部分分开。EPS_SVR =103,//ε-支持向量回归。来自训练集的特征向量和拟合超平面之间的距离必须小于p。对于异常值，使用惩罚乘数 C。NU_SVR =104 // ν-支持向量回归。 ν用于代替 p。
}
virtual void cv::ml::SVM::setType(int val)

Python：

cv.ml_SVM.setType(val) ->None

设置参数C

根据"2.基本原理"中对参数C的介绍，我们应该如何设置参数C？

C值较大时：误分类错误较少，但余量较小。这种情况下，侧重于寻找具有很少的误分类错误的超平面。
C值较小时：具有更大余量和更多分类错误。在这种情况下，更侧重于寻找具有大余量的超平面。

C++:

//设置参数C
virtual void cv::ml::SVM::setC(double val)

python:

cv.ml_SVM.setC(val) -> None

设置核函数

C++:

enum KernelTypes {CUSTOM =-1,//由SVM::getKernelType返回，默认是RBFLINEAR =0,//线性内核，速度最快POLY =1,//多项式核RBF =2,//径向基函数（RBF），大多数情况下是个不错的选择SIGMOID =3,//sigmoid核CHI2 =4,//Chi2核，类似于RBF核INTER =5//直方图交叉核，速度较快
}
virtual void cv::ml::SVM::setKernel(int kernelType)

python:

cv.ml_SVM.setKernel(kernelType) -> None

设置迭代算法的终止标准

C++:

virtual void cv::ml::SVM::setTermCriteria(const cv::TermCriteria &val)    // cv::TermCriteria
cv::TermCriteria::TermCriteria (int type,int maxCount,double epsilon)// Type 
enum  cv::TermCriteria::Type {COUNT =1,MAX_ITER =COUNT,//最大迭代次数EPS =2 //迭代算法停止时所需的精度或参数变化
}

python:

cv.ml_SVM.setTermCriteria(val) ->None

训练SVM模型

trainAuto方法通过选择最佳参数 C、gamma、p、nu、coef0、degree 来自动训练 SVM 模型。当测试集误差的交叉验证估计最小时，参数被认为是最佳的。此函数仅使用SVM::getDefaultGrid进行参数优化，因此仅提供基本的参数选项。

trainAuto函数适用于分类（SVM::C_SVC或SVM::NU_SVC）以及回归（SVM::EPS_SVR或SVM::NU_SVR）。如果是SVM::ONE_CLASS，则不进行优化，并执行带有 params 中指定参数的常用 SVM。

C++：

//输入由TrainData::create或TrainData::loadFromCSV构造的训练数据
virtual bool cv::ml::SVM::trainAuto(const Ptr<TrainData> & data,
int     kFold = 10,
ParamGrid     Cgrid = getDefaultGrid(C),
ParamGrid     gammaGrid = getDefaultGrid(GAMMA),
ParamGrid     pGrid = getDefaultGrid(P),
ParamGrid     nuGrid = getDefaultGrid(NU),
ParamGrid     coeffGrid = getDefaultGrid(COEF),
ParamGrid     degreeGrid = getDefaultGrid(DEGREE),
bool     balanced = false 
)    //输入训练样本
bool cv::ml::SVM::trainAuto(InputArray samples,int     layout,InputArray     responses,int     kFold = 10,Ptr< ParamGrid >     Cgrid = SVM::getDefaultGridPtr(SVM::C),Ptr< ParamGrid >     gammaGrid = SVM::getDefaultGridPtr(SVM::GAMMA),Ptr< ParamGrid >     pGrid = SVM::getDefaultGridPtr(SVM::P),Ptr< ParamGrid >     nuGrid = SVM::getDefaultGridPtr(SVM::NU),Ptr< ParamGrid >     coeffGrid = SVM::getDefaultGridPtr(SVM::COEF),Ptr< ParamGrid >     degreeGrid = SVM::getDefaultGridPtr(SVM::DEGREE),bool     balanced = false 
)

Python：

cv.ml_SVM.trainAuto(samples, layout, responses[, kFold[, Cgrid[, gammaGrid[, pGrid[, nuGrid[, coeffGrid[, degreeGrid[, balanced]]]]]]]]) -> retval

参数：

samples：训练样本
layout：参考 ml::SampleTypes，如cv.ml.ROW_SAMPLE表示每个训练样本是行向量，cv.ml.COL_SAMPLE表示每个训练样本是列向量
responses：与训练样本有关的响应向量
kFold：k交叉验证，训练集会分成k个子集，从中选取一个用来测试，剩余k-1个用来训练
balanced：如果设为True且是2-class分类问题，方法会自动创建更平衡的交叉验证子集，即子集中的类之间比例接近整个训练数据集中的比例

预测结果

C++：

// 预测输入样本的响应结果
virtual float predict(InputArray  samples,                  // input samples, float matrixOutputArray results = cv::noArray(),  // optional output results matrixint         flags   = 0               // (model-dependent)
) const = 0;

python：

cv.ml_StatModel.predict(samples[, results[, flags]]) ->retval, results

误差计算

对于回归模型，误差计算为 RMS；对于分类器，误差计算为错误分类样本的百分比 (0%-100%)。
C++：

// 在训练集或测试集上计算误差
virtual float calcError(const Ptr<TrainData>& data, // training samplesbool test, // true: compute over test set// false: compute over training setcv::OutputArray resp  // the optional output responses
) const;

python：

cv.ml_StatModel.calcError(data, test[, resp]) ->retval, resp

保存SVM模型

C++：

void cv::Algorithm::save(const String &filename)  const

Python：

cv.Algorithm.save(filename) ->None

从文件中加载SVM

C++：

static Ptr<SVM> cv::ml::SVM::load(const String &filepath)

Python：

cv.ml.SVM_load(filepath) ->retval

4. 示例代码

官方示例（python）

在这里插入图片描述
构造数据，用来模拟训练集中的两个类别：

from __future__ import print_function
import cv2 as cv
import numpy as np
import random as rng
import time
from matplotlib import pyplot as pltNTRAINING_SAMPLES = 100 # 每个类别的训练样本数
FRAC_LINEAR_SEP = 0.9   # 线性可分的样本比例# 准备用于数据可视化
WIDTH = 512
HEIGHT = 512
I = np.zeros((HEIGHT, WIDTH, 3), dtype=np.uint8)# 设置训练样本
trainData = np.empty((2*NTRAINING_SAMPLES, 2), dtype=np.float32)
labels = np.empty((2*NTRAINING_SAMPLES, 1), dtype=np.int32)rng.seed(100) # Random value generation class# 线性可分的训练样本数量
nLinearSamples = int(FRAC_LINEAR_SEP * NTRAINING_SAMPLES)## [setup1]
# 生成class 1的随机点，随机点的x坐标在[0, 0.4)，y坐标在 [0, 1)
trainClass = trainData[0:nLinearSamples,:]
# The x coordinate of the points is in [0, 0.4)
c = trainClass[:,0:1]
c[:] = np.random.uniform(0.0, 0.4 * WIDTH, c.shape)
# The y coordinate of the points is in [0, 1)
c = trainClass[:,1:2]
c[:] = np.random.uniform(0.0, HEIGHT, c.shape)# 生成class 2的随机点，随机点的x坐标在[0.6, 1]，y坐标在 [0, 1)
trainClass = trainData[2*NTRAINING_SAMPLES-nLinearSamples:2*NTRAINING_SAMPLES,:]
# The x coordinate of the points is in [0.6, 1]
c = trainClass[:,0:1]
c[:] = np.random.uniform(0.6*WIDTH, WIDTH, c.shape)
# The y coordinate of the points is in [0, 1)
c = trainClass[:,1:2]
c[:] = np.random.uniform(0.0, HEIGHT, c.shape)# 设置线性不可分的训练样本 
# Generate random points for the classes 1 and 2
trainClass = trainData[nLinearSamples:2*NTRAINING_SAMPLES-nLinearSamples,:]
# x坐标在 [0.4, 0.6)，y坐标在[0, 1)
c = trainClass[:,0:1]
c[:] = np.random.uniform(0.4*WIDTH, 0.6*WIDTH, c.shape)
c = trainClass[:,1:2]
c[:] = np.random.uniform(0.0, HEIGHT, c.shape)# 设置两个类别的label
labels[0:NTRAINING_SAMPLES,:] = 1                   # Class 1
labels[NTRAINING_SAMPLES:2*NTRAINING_SAMPLES,:] = 2 # Class 2

设置SVM参数，初始化模型：

print('Starting training process')
svm = cv.ml.SVM_create()
svm.setType(cv.ml.SVM_C_SVC)
svm.setC(0.1)
svm.setKernel(cv.ml.SVM_LINEAR)
svm.setTermCriteria((cv.TERM_CRITERIA_MAX_ITER, int(1e7), 1e-6))

训练SVM：

## 训练
svm.train(trainData, cv.ml.ROW_SAMPLE, labels)
print('Finished training process')## 显示决策区域
green = (0,100,0)
blue = (100,0,0)
for i in range(I.shape[0]):for j in range(I.shape[1]):sampleMat = np.matrix([[j,i]], dtype=np.float32)response = svm.predict(sampleMat)[1]if response == 1:I[i,j] = greenelif response == 2:I[i,j] = blue

对训练集中两个类别的样本进行可视化：

## 用两种颜色圆圈表示class 1和class 2的训练数据
thick = -1
# Class 1
for i in range(NTRAINING_SAMPLES):px = trainData[i,0]py = trainData[i,1]cv.circle(I, (px, py), 3, (0, 255, 0), thick)# Class 2
for i in range(NTRAINING_SAMPLES, 2*NTRAINING_SAMPLES):px = trainData[i,0]py = trainData[i,1]cv.circle(I, (px, py), 3, (255, 0, 0), thick)# 显示支持向量（
## [show_vectors]
thick = 2
sv = svm.getUncompressedSupportVectors()for i in range(sv.shape[0]):cv.circle(I, (sv[i,0], sv[i,1]), 6, (128, 128, 128), thick)
## [show_vectors]#cv.imwrite('result.png', I)                      # save the Image
#cv.imshow('SVM for Non-Linear Training Data', I) # show it to the user
plt.imshow(I)

推理阶段（C++版本）

void test_svm(std::string videopath, std::string svm_file = "svm.mat")
{/// 加载svm模型参数cv::Ptr<cv::ml::SVM> svm = cv::ml::SVM::load(svm_file);/// 初始化特征提取器// 此处省略……cv::VideoCapture cap(videopath);if (cap.isOpened()){cv::Mat src;//imgint sleep_interval = 1;//每隔多少ms取帧int frameIdx = 0;while (true){if (!cap.read(src)){break;}frameIdx++;double start = static_cast<double>(cv::getTickCount());cv::Mat flowFeat;//提取运动特征m_featureExtactor.ProcessFlow(src, flowFeat);flowFeat.convertTo(flowFeat, CV_32FC1);//获取分类结果int response = (int)svm->predict(flowFeat);cv::putText(src, cv::String(std::to_string(response)), cv::Point(20,20), cv::FONT_HERSHEY_PLAIN, 1, cv::Scalar(0, 255, 0));  //计算耗时float times = ((float)cv::getTickCount() - start) / cv::getTickFrequency();std::cout << "time cost: " << times << " s." << std::endl;cv::imshow("img", src);if (cv::waitKey(1) == 27) {break;}}}
}

5. 小结

本文整理了Opencv中SVM支持向量机的原理、函数和代码示例。

如果对你有帮助的话，欢迎一键三连支持下博主~

Chih-Chung Chang and Chih-Jen Lin. Libsvm: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST), 2(3):27, 2011. ↩︎
《机器学习》周志华 ↩︎ ↩︎ ↩︎
https://docs.opencv.org/4.5.3/d4/db1/tutorial_py_svm_basics.html ↩︎
https://docs.opencv.org/4.5.3/d1/d2d/classcv_1_1ml_1_1SVM.html ↩︎