一、学习目标

（1）了解最优化模型。

（2）掌握线性规划的优化求解。

（3）掌握整数规划的优化求解。

（4）了解Matlab的图形化应用。

二、实例演练

     1、谈谈你对最优化模型的了解。

        最优化模型是数学建模大赛中最常见的问题类型之一。一般说来，凡是寻求最大、最小、最远、最近、最经济、最丰富、最高效、最耗时的目标，都可以划入优化问题的范畴。MATLAB 优化工具箱和全局优化工具箱对多个优化问题提供了完整的解决方案，前者涵盖了线性规划、混合整型线性规划、二次规划、非线性优化、非线性最小二乘的求解器，后者囊括了全局搜索、多初始点、模式搜索、遗传算法等求解算法。

       最优化即在一定的条件下，寻求使目标最小（大）的设计参数或决策。在优化问题中有两个关键对象：目标函数和约束条件。哈哈哈，这让笔者想起来高中学到的线性规划，其实，本节谈到的最优化模型跟高中的线性规划还真有点像。不过，高中的线性规划问题约束条件很少，一般是通过作图法来求解。本节的最优化模型约束条件一般比高中的线性规划多很多，并且我们要通过写代码去求解，而不是作图。常规优化问题，其数学表达可以描述为：

其中x 为长度n的决策变量向量，f(x) 为目标函数，G(x) 为约束函数。

以上数学表达式看不明白也没关系，因为下面我们会通过两个具体的例子去讲解分析。

求解目标函数的最小（大）值，一个高效而精确的解决方案不仅取决于约束条件和变量数量，更取决于目标函数和约束函数的特性。明确优化类型是确认优化方案的前提，让我们看一下这些特性如何划分：

常见的目标函数有：

线性规划：被广泛的应用于变量之间可线性表示的财务、能源、运营研究等现代管理领域中。

混合整数线性规划：扩展了线性规划问题，增加了最优解中部分或全部变量必须是整数的约束。例如，如果一个变量代表要认购的股票数量，则只应取整数值。同样，如果一个变量代表发电机的开/关状态，则只应取二进制值（0 或 1）。

二次规划：目标函数或约束函数为多元二次函数。此优化应用于财务金融中投资组合优化、发电厂发电优化、工程中设计优化等领域。

最小二乘：分为线性和非线性，通过最小化误差的平方和寻找变量的最优函数匹配。非线性最小二乘优化还可用于曲线拟合。

 

对 MATLAB 提供的各类优化问题的算法，我们称之为求解器（Solver）。根据其求解目标，被分为四大组：

• 极小值优化组：找到目标函数出发点 x0 附近的局部极小值

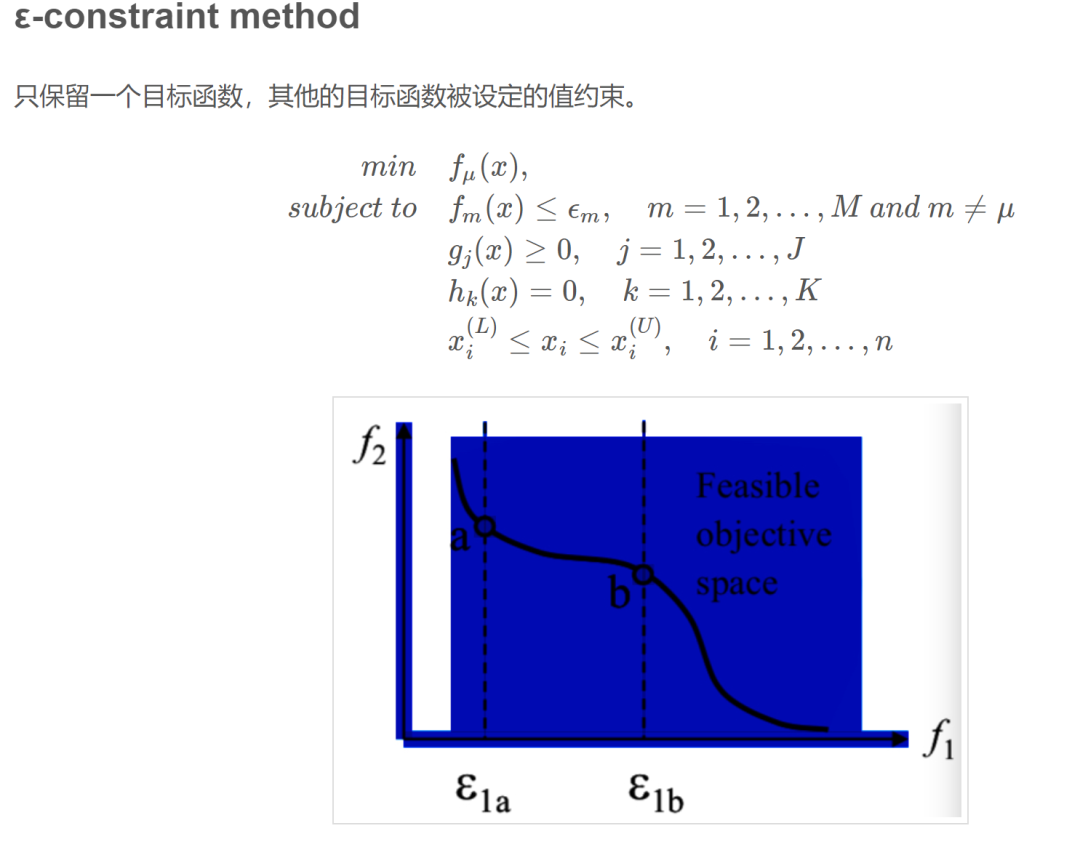
• 多目标优化组：找到最小化一组函数的最大值或指定的值

• 方程求解组：找到非线性方程 f(x) = 0 出发点 x0 附近的解

• 最小二乘法（曲线拟合）组：最小化平方和

仅优化工具箱就提供了近 20 种求解器，面对如此繁多的选项，用户往往一头雾水。幸好，MATLAB 提供了简单明了的参考工具 —— 优化决策表。可谓一表在手，优化不愁：

上表中*表示算法由全局工具箱提供。

我的天呀，你是不是已经被上面的内容吓傻了。看不太懂？没关系。我们现在只需知道有那么一回事即可，不必苦恼。等遇到相应的问题时我们再去结合具体的例子去深入学习和理解。

    2、已知目标函数和约束条件如下，试求解目标函数的最小值。

                             

       初一看，HPS、PP、EP、P1、I1，……等等，这些是什么东东？别紧张，它们只是变量，把它们当成x,y,z这种常见的变量去看待即可。我数了一下，约束函数中共有19条数学表达式，涉及16个变量。是挺难搞的，用高中的作图法怕是解决不了。别怕，我们有Matlab，通过代码去搞定它。

       好，现在我们开始一步步去求解它。

a. 首先，根据题目确认这是一个线性规划问题。而线性规划的通用数学表达式和MATLAB标准形式为：

这个标准形式很重要，上面的A,b,Aeq,beq,lb,ub我们后面要用到。

b. 对于线性规划的优化求解步骤（也适用于其他优化方案），建议如下：

    1 ) 选择优化求解器

    2 ) 将所有变量合并为一个向量

    3 ) 创建边界约束（lb，ub）

    4 ) 创建线性不等式约束（A，b）

    5 ) 创建线性等式约束（Aeq，beq）

    6 ) 创建目标函数

    7 ) 优化问题求解

    8 ) 结果检验

上面的求解步骤非常重要，我们的代码整体框架跟求解步骤差不多。

现在我们按照上面的求解步骤去求解：

（1）选择优化求解器。

这道题目是这是一个线性规划问题。求解线性规划问题，我们一般选用linprog。linprog在写代码将要写完才需用到。在第一步我们只需要知道一个线性规划问题，代码按照求解线性规划问题去写即可。

（2）将所有变量合并为一个向量。

目标函数和约束条件中共有HPS、PP、EP、P1、I1等16个变量，我们需要将其合并为一个向量。除了合并为一个向量外，我们还将每个变量依次分别赋值1,2,3,4，……16。

%% 将所有变量合并为一个向量，共16个变量
variables = {'I1','I2','HE1','HE2','LE1','LE2','C','BF1','BF2','HPS','MPS','LPS','P1','P2','PP','EP'}
N = length(variables)
for v = 1:Neval([variables{v},'=',num2str(v),';'])
end

（3）创建边界约束（lb，ub）

lb是指low boundary，即最低边界。ub是指up boundary，即最高边界。在这一步中，我们需要把约束条件里的不等式(该不等式只含单个变量，如2500<=P1<=6250,3000<=P2<=9000)找出来，并根据它们的上下边界写代码。

%% 设置上下限约束(lb<=x<=ub)
% 设置下限约束，即lb<=x
lb = zeros(size(variables)); % 1x16的矩阵，每个数都是0
lb([P1,P2,MPS,LPS]) = [2500,3000,271536,100623];
% 设置上限约束，即x<=ub
ub = Inf(size(variables)); % 1想6的矩阵，每个数都是无穷大
ub([P1,P2,I1,I2,C,LE2])= [6250,9000,192000,244000,62000,142000];

（4）创建线性不等式约束（A，b）。

在这一步需要将约束条件里的不等式(该不等式含两个或两个以上变量)找出来，并根据它们的上下边界写代码。

%% 创建线性不等式约束(A*x<=b)
A = zeros(3,16); % 3x16的矩阵，每个数均为0,为什么是3x16，因为约束条件有3个不等式
% 由不等式I1-HE1<=132000得到下面一行代码
A(1,I1)=1; A(1,HE1)=-1; b(1) = 132000;
% 由不等式-EP-PP<=12000得到下面一行代码
A(2,EP)=-1; A(2,PP)=-1; b(2) = -12000;
% 由不等式-P1-P2-PP<=-24550得到下面一行代码
A(3,[P1,P2,PP])=[-1,-1,-1];b(3)=-24550;

（5）创建线性等式约束（Aeq，beq）。

在这一步需要把约束条件中的等式找出来，并通过移项，让等式的右边为0。

%% 创建线性等式约束(Aeq*x=beq)
Aeq=zeros(8,16);beq=zeros(8,1) % 约束条件中共有8个等式
% 把等式I2=LE2+HE2转化为LE2+HE2-I2=0后，得到下面一行代码
Aeq(1,[LE2,HE2,I2])=[1,1,-1];
Aeq(2,[LE1,LE2,BF2,LPS])=[1,1,1,-1];
Aeq(3,[I1,I2,BF1,HPS])=[1,1,1,-1];
Aeq(4,[C,MPS,LPS,HPS])=[1,1,1,-1];
Aeq(5,[LE1,HE1,C,I1])=[1,1,1,-1];
Aeq(6,[HE1,HE2,BF1,BF2,MPS])=[1,1,1,-1,-1];
Aeq(7,[HE1,LE1,C,P1,I1])=[1267.8,1251.4,192,3413,-1359.8];
Aeq(8,[HE2,LE2,P2,I2])=[1267.8,1251.4,3413,-1359.8];

（6）创建目标函数。

%% 创建目标函数
f = zeros(size(variables));
% 由目标函数0.002614HPS+0.0239PP+0.009825EP
f([HPS,PP,EP]) = [0.002614,0.0239,0.009825];

（7） 求解问题

%% 由linprog实现线性规划问题求解
options = optimoptions('linprog','Algorithm','dual-simplex');
% 将前面已经确定的各个参数传入linprog()中
[x, fval] = linprog(f,A,b,Aeq,beq,lb,ub,options);
for d=1:Nfprintf('%12.2f\t%s\n',x(d),variables{d})
end

fprintf函数是将求解后每个变量的打印出来。

求解结果如下：

下面把完整的源代码贴上：

clc,clear,close all
%% 选择优化求解器，线性规划求解可由linprog实现%% 将所有变量合并为一个向量，共16个变量
variables = {'I1','I2','HE1','HE2','LE1','LE2','C','BF1','BF2','HPS','MPS','LPS','P1','P2','PP','EP'}
N = length(variables)
for v = 1:Neval([variables{v},'=',num2str(v),';'])
end%% 设置上下限约束(lb<=x<=ub)
% 设置下限约束，即lb<=x
lb = zeros(size(variables)); % 1x16的矩阵，每个数都是0
lb([P1,P2,MPS,LPS]) = [2500,3000,271536,100623];
% 设置上限约束，即x<=ub
ub = Inf(size(variables)); % 1想6的矩阵，每个数都是无穷大
ub([P1,P2,I1,I2,C,LE2])= [6250,9000,192000,244000,62000,142000];%% 创建线性不等式约束(A*x<=b)
A = zeros(3,16); % 3x16的矩阵，每个数均为0,为什么是3x16，因为约束条件有3个不等式
% 由不等式I1-HE1<=132000得到下面一行代码
A(1,I1)=1; A(1,HE1)=-1; b(1) = 132000;
% 由不等式-EP-PP<=12000得到下面一行代码
A(2,EP)=-1; A(2,PP)=-1; b(2) = -12000;
% 由不等式-P1-P2-PP<=-24550得到下面一行代码
A(3,[P1,P2,PP])=[-1,-1,-1];b(3)=-24550;%% 创建线性等式约束(Aeq*x=beq)
Aeq=zeros(8,16);beq=zeros(8,1) % 约束条件中共有8个等式
% 把等式I2=LE2+HE2转化为LE2+HE2-I2=0后，得到下面一行代码
Aeq(1,[LE2,HE2,I2])=[1,1,-1];
Aeq(2,[LE1,LE2,BF2,LPS])=[1,1,1,-1];
Aeq(3,[I1,I2,BF1,HPS])=[1,1,1,-1];
Aeq(4,[C,MPS,LPS,HPS])=[1,1,1,-1];
Aeq(5,[LE1,HE1,C,I1])=[1,1,1,-1];
Aeq(6,[HE1,HE2,BF1,BF2,MPS])=[1,1,1,-1,-1];
Aeq(7,[HE1,LE1,C,P1,I1])=[1267.8,1251.4,192,3413,-1359.8];
Aeq(8,[HE2,LE2,P2,I2])=[1267.8,1251.4,3413,-1359.8];%% 创建目标函数
f = zeros(size(variables));
% 由目标函数0.002614HPS+0.0239PP+0.009825EP
f([HPS,PP,EP]) = [0.002614,0.0239,0.009825];%% 由linprog实现线性规划问题求解
options = optimoptions('linprog','Algorithm','dual-simplex');
% 将前面已经确定的各个参数传入linprog()中
[x, fval] = linprog(f,A,b,Aeq,beq,lb,ub,options);
for d=1:Nfprintf('%12.2f\t%s\n',x(d),variables{d})
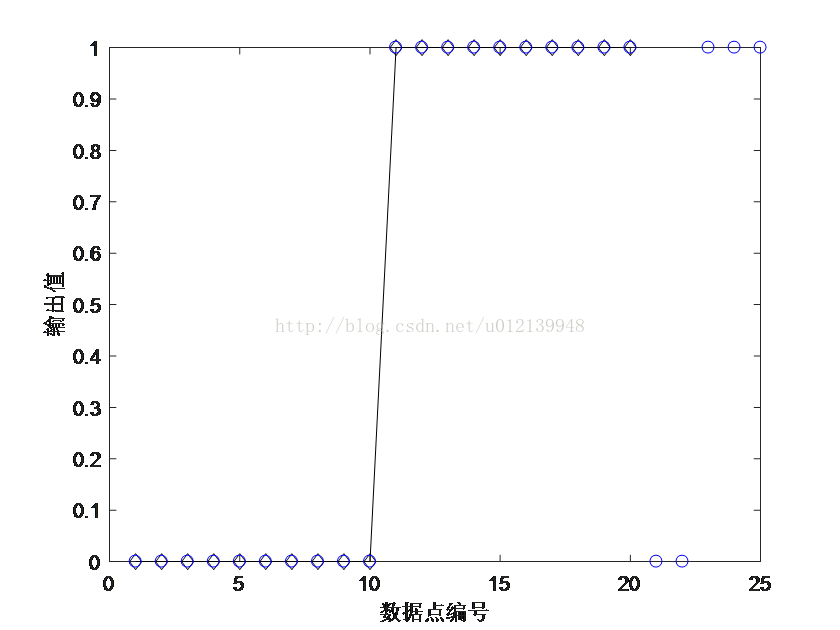
end

  3、下面是一个整数规划问题，已知目标函数和约束条件如下，求解目标函数的最大值。

                                      

     求解最大值问题和求解最小值问题本质上是一致的，求解最大值也可以转换为求解最小值。

例如：本题要求解z=3*x1-2*x2+5*x3的最大值，也就是要求解y=-3*x1+2*x2-5*x3的最小值。求解线性规划最小值问题我们在上面已经学过。本题还有一个比较特殊的问题是，约束条件中的三个变量均为整数，而且是0或1，这也是所谓的0-1规划问题。

求解整值问题要用到专门的求解器 intlinprog。

clc,clear,close all
% 求z=3*x1 - 2*x2 + 5*x3的最大值转化为求y=-3*x1 + 2*x2 - 5*x3的最小值。
f = [-3;2;-5]; % 创建目标函数
intcon=[1,2,3];
A=[1 2 -1; 1 4 1; 1 1 0; 0 4 1]; % 四个不等式中的变量系数
b=[2;4;3;6]; % 约束条件中不等式右边的常数
lb=[0,0,0]; % x1,x2,x3=0
ub=[1,1,1]; % x1,x2,x3=1
Aeq=[0,0,0];
beq=0;
x=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)

我想提一下intcon=[1,2,3]这句代码是怎么回事。

下面我举一个简单的例子来说明intcon的用法。

X=[x1,x2,x3,x4,x5,x6]，其中x2, x3, x6只能取整数
intcon = [2,3,6]
如果所有变量都只能取整数，则：intcon = [1,2,3,4,5,6]; 比较方便的写法是:intcon = 1:6
如果只有x4取整数，则：intcon = 4;就是约束整形变量

在本题中，除了x1,x2,x3=0或1外，没有其它的等式了。故Aeq=[0,0,0];beq=0;

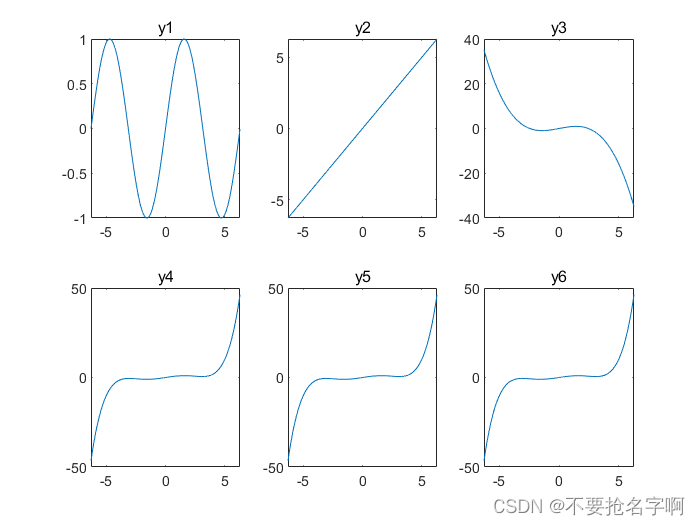
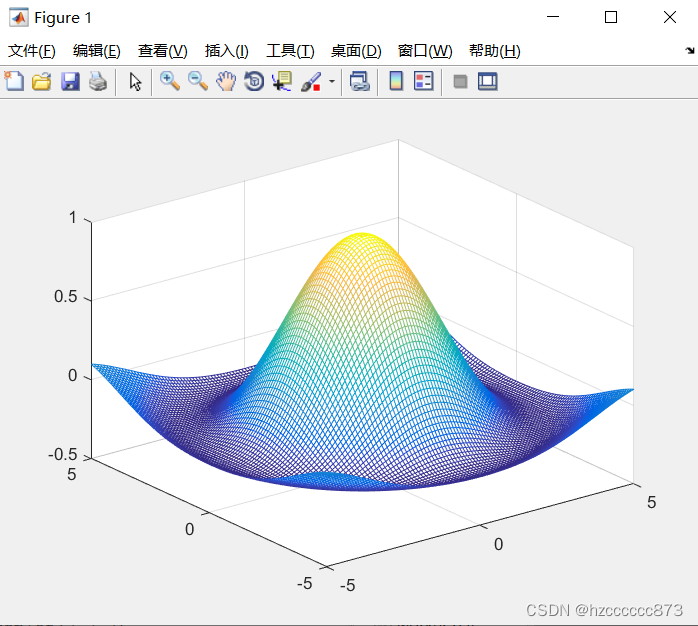
 4、图形化应用

在数学建模竞赛中，我们一般通过代码来进行求解问题，图形化应用可以用来检验结果是否正确。

MATLAB 在数据分析领域如此受欢迎，除了其提供丰富的内置算法集，还有各类友好的应用界面。在优化工具箱中，也有这么一个强大的工具—— Optimization App，可以在 MATLAB Apps 窗口或者运行 optmitool 命令打开。它是一个交互式的图形化应用工具，无需手写代码，直接在图形界面中设置各类求解器、配置目标函数、约束条件，即可运行优化算法并使中间结果和最终结果可视化。

在 Optimization App 中，只需点击菜单栏中的 File > Generate Code，即可将 App 中的各项设置自动生成 MATLAB 代码，用户可实现算法的复用和二次开发。