【数学建模】常用模型算法及MATLAB代码汇总

article/2025/9/16 16:02:16

大家好，我是程序员史迪仔。

这篇文章是在大学准备数学建模比赛时，整理的学习笔记，没想到阅读量、点赞量和收藏量还是可以的，很高兴我的文章能给大家带来帮助！

    • 一、蒙特卡洛算法
    • 二、数据拟合
    • 三、数据插值
    • 四、图论
      • 1、最短路问题
        • （1）Dijkstra算法
        • （2）Floyd算法



一、蒙特卡洛算法

1、定义

蒙特卡洛算法是以概率和统计的理论、方法为基础的一种数值计算方法，将所求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解，故又称随机抽样法或统计实验法。


2、适用范围

可以较好的解决多重积分计算、微分方程求解、积分方程求解、特征值计算和非线性方程组求解等高难度和复杂的数学计算问题。


3、特点

蒙特卡洛算法可以应用在很多场合，但求的是近似解，在模拟样本越大的情况下，越接近于真实值，单样本数增加会带来计算量的大幅上升。对于一些简单问题来说，蒙特卡洛是个笨办法，但对于许多问题来说，它往往是个有效，有时甚至是唯一可行的方法。


4、举例

y = x^2 ，y = 12 - x 与 X 轴在第一象限与 X 轴围成一个曲边三角形。设计一个随机试验，求该图形的近似值。


（1）作图
在这里插入图片描述
Code：

%作图
x = 0:0.25:12;
y1 = x.^2;
y2 = 12 - x;
plot(x, y1, x, y2)
xlabel('x');ylabel('y');
%产生图例
legend('y1=x^2', 'y2=12-x');
title('蒙特卡洛算法');
%图中x轴和y轴的范围，中括号前面是y轴范围，中括号后面是x轴范围
axis([0 15 0 15]);
text(3, 9, '交点');
%加上网格线
grid on

（2）设计的随机试验的思想：在矩形区域[0,12]*[0.9]上产生服从均与分布的10^7个随机点，统计随机点落在曲边三角形内的个数，则曲边三角形的面积近似于上述矩形的面积乘以频率。

Code：

%蒙特卡洛算法的具体实现
%产生一个1行10000000列的矩阵，矩阵中每个数是从0到12之间随机取
x = unifrnd(0, 12, [1, 10000000]);
y = unifrnd(0, 9, [1, 10000000]);
frequency = sum(y<x.^2&x<=3)+ sum(y<12-x&x>=3);
area = 12*9*frequency/10^7;
disp(area);

所求近似值：
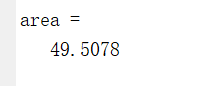
在这里插入图片描述


参考博客：https://blog.csdn.net/u013414501/article/details/50478898



二、数据拟合

1、定义

已知有限个数据点，求近似函数，可不过已知数据点，只要求在某种意义下它在这些点上的总偏差最小，从而能较好的反应数据的整体变化趋势。


2、常用方法

  • 一般采用最小二乘法。
  • 拟合的实现分为 MATLAB 和 excel 实现。MATLAB 的实现就是 polyfit 函数，主要是多项式拟合。

3、举例

(1) 数据如下：

   序号 	x         y       z1	426.6279	0.066	2.8978672	465.325	    0.123   1.6215693	504.0792	0.102	2.4292274	419.1864	0.057	3.505545	464.2019	0.103	1.1539216	383.0993	0.057	2.2971697	416.3144	0.049	3.0589178	464.2762	0.088	1.3698589	453.0949	0.09	3.02874110	376.9057	0.049	4.04724111	409.0494	0.045	4.83814312	449.4363	0.079	4.12097313	372.1432	0.041	3.60479514	389.0911	0.085	2.04892215	446.7059	0.057	3.37260316	347.5848	0.03	4.64301617	379.3764	0.041	4.7417118	453.6719	0.082	1.84144119	388.1694	0.051	2.29353220	444.9446	0.076	3.54180321	437.4085	0.056	3.98476522	408.9602	0.078	2.29196723	393.7606	0.059	2.91039124	443.1192	0.063	3.08052325	514.1963	0.153	1.31474926	377.8119	0.041	3.96758427	421.5248	0.063	3.00571828	421.5248	0.063	3.00571829	421.5248	0.063	3.00571830	421.5248	0.063	3.00571831	421.5248	0.063	3.00571832	421.5248	0.063	3.00571833	421.5248	0.063	3.00571834	421.5248	0.063	3.00571835	421.5248	0.063	3.00571836	421.5248	0.063	3.00571837	416.1229	0.111	1.28164638	369.019	    0.04	2.86120139	362.2008	0.036	3.06099540	417.1425	0.038	3.69532

(2) 方法一：使用MATLAB编写代码

%读取表格
A = xlsread('E:\表格\1.xls', 'Sheet1', 'A1:AN2');
B = A;
[I, J] = size(B);%数据拟合
%x为矩阵的第一行，y为矩阵的第二行
x = A(1,:);
y = A(2,:);
%polyfit为matlab中的拟合函数，第一个参数是数据的横坐标
%第二个参数是数据的纵坐标，第三个参数是多项式的最高阶数
%返回值p中包含n+1个多项式系数
p = polyfit(x, y, 2);
disp(p);
%下面是作图的代码
x1 = 300:10:600;
%polyval是matlab中的求值函数，求x1对应的函数值y1
y1 = polyval(p,x1);
plot(x,y,'*r',x1,y1,'-b');
%plot(x,'DisplayName','x','YDataSource','x');
%figure(gcf);

(3) 方法三：使用matlab的图形化拟合包（推荐）


  • 将数据导入工作区并通过cftool命令打开matlab的图形化拟合包
    在这里插入图片描述

  • 选择x、y变量
    在这里插入图片描述

  • 选择拟合方式和最高项次数
    在这里插入图片描述

  • 得到拟合结果
    在这里插入图片描述

使用图形化拟合工具不仅简单快捷，还可以使用多种拟合方式，寻找到最好的拟合曲线。



三、数据插值

1、定义

  • 在离散数据的基础上补插连续函数，使得这条连续曲线通过给定的全部离散数据点。即求过已知有限个数据点的近似函数。

  • 从定义上看，插值和拟合有一定的相似度，但插值要求近似函数通过给定的所有离散数据，而拟合并不要求这样，只要近似函数能较好的反映数据变化的趋势即可（近似含义不同），当测量值是准确的，没有误差时，一般用插值；当测量值与真实值有误差时，一般用数据拟合。


2、作用

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值情况，估算出函数在其他点处的近似值。


3、举例

%years、service和wage是原始数据
years = 1950:10:1990;
service = 10:10:30;
wage = [ 150.697  199.592  187.625  179.323  195.072; 250.287  203.212  179.092  322.767  226.505;153.706  426.730  249.633  120.281  598.243];
[X, Y] = meshgrid(years, service);
% % 三维曲线
% plot3(X, Y, wage)
% 三维曲面
figure
surf(X, Y, wage)
%interp2是matlab中的二维插值函数，前两个参数是已知位置，后两个是未知位置，w是未知位置的插值结果
w = interp2(service,years,wage,15,1975);

在这里插入图片描述

可参考：数学建模常用模型02 ：插值与拟合



四、图论

1、最短路问题

最短路问题就是选择一条距离最短的路线。

例如：一名货柜车司机奉命在最短的时间内将一车货物从甲地运往乙地。从甲地到乙地的公路网纵横交错，因此有多种行车路线，这名司机应选择哪条线路呢？假设货柜车的运行速度是恒定的，那么这一问题相当于需要找到一条从甲地到乙地的最短路。（Dijkstra算法）

具体介绍见这里：最短路径—Dijkstra算法和Floyd算法


（1）Dijkstra算法

先给出一个无向图
在这里插入图片描述

用Dijkstra算法找出以A为起点的单源最短路径步骤如下
在这里插入图片描述


代码模板：

#include<iostream>  
#include<cstdio>  
#include<cstdlib>  
#include<cmath>  
#include<cstring>  
#include<algorithm>  
#include<vector>  
#include<fstream>  
using namespace std;  const int maxnum = 100;  
const int maxint = 2147483647;  
int dist[maxnum];     // 表示当前点到源点的最短路径长度  
int prev[maxnum];     // 记录当前点的前一个结点  
int c[maxnum][maxnum];   // 记录图的两点间路径长度  
int n, line;             // n表示图的结点数，line表示路径个数  
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])  
{  bool s[maxnum];    // 判断是否已存入该点到S集合中  for(int i=1; i<=n; ++i)  {  dist[i] = c[v][i];  s[i] = 0;     // 初始都未用过该点  if(dist[i] == maxint)  prev[i] = 0;  else  prev[i] = v;  }  dist[v] = 0;  s[v] = 1;  // 依次将未放入S集合的结点中，取dist[]最小值的结点，放入结合S中  // 一旦S包含了所有V中顶点，dist就记录了从源点到所有其他顶点之间的最短路径长度  for(int i=2; i<=n; ++i)  {  int tmp = maxint;  int u = v;  // 找出当前未使用的点j的dist[j]最小值  for(int j=1; j<=n; ++j)  if((!s[j]) && dist[j]<tmp)  {  u = j;              // u保存当前邻接点中距离最小的点的号码  tmp = dist[j];  }  s[u] = 1;    // 表示u点已存入S集合中  // 更新dist  for(int j=1; j<=n; ++j)  if((!s[j]) && c[u][j]<maxint)  {  int newdist = dist[u] + c[u][j];  if(newdist < dist[j])  {  dist[j] = newdist;  prev[j] = u;  }  }  }  
}  
void searchPath(int *prev,int v, int u)  
{  int que[maxnum];  int tot = 1;  que[tot] = u;  tot++;  int tmp = prev[u];  while(tmp != v)  {  que[tot] = tmp;  tot++;  tmp = prev[tmp];  }  que[tot] = v;  for(int i=tot; i>=1; --i)  if(i != 1)  cout << que[i] << " -> ";  else  cout << que[i] << endl;  
}  int main()  
{  //freopen("input.txt", "r", stdin);  // 各数组都从下标1开始  // 输入结点数  cin >> n;  // 输入路径数  cin >> line;  int p, q, len;          // 输入p, q两点及其路径长度  // 初始化c[][]为maxint  for(int i=1; i<=n; ++i)  for(int j=1; j<=n; ++j)  c[i][j] = maxint;  for(int i=1; i<=line; ++i)  {  cin >> p >> q >> len;  if(len < c[p][q])       // 有重边  {  c[p][q] = len;      // p指向q  c[q][p] = len;      // q指向p，这样表示无向图  }  }  for(int i=1; i<=n; ++i)  dist[i] = maxint;  for(int i=1; i<=n; ++i)  {  for(int j=1; j<=n; ++j)  printf("%-16d", c[i][j]);  printf("\n");  }  Dijkstra(n, 1, dist, prev, c);   //仅调用函数求出了源点到其他点的距离 改法:Dijkstra(n, x, dist, prev, c);  其中x=1,2,3,4,...,n  //    for(int i=1; i<=n; ++i)   //dist存储了源点到其他点的距离情况  
//    {  
//        printf("%-16d", dist[i]);  
//    }  printf("\n");  // 最短路径长度  cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;  // 路径  cout << "源点到最后一个顶点的路径为: ";  searchPath(prev, 1, n);  return 0;  
}  /* 
输入数据: 5 7 1 2 10 1 4 30 1 5 100 2 3 50 3 5 10 4 3 20 4 5 60 输出数据: 999999 10 999999 30 100 10 999999 50 999999 999999 999999 50 999999 20 10 30 999999 20 999999 60 100 999999 10 60 999999 源点到最后一个顶点的最短路径长度: 60 源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5 
*/

（2）Floyd算法

#include<iostream>  
#include<cstdio>  
#include<cstdlib>  
#include<cmath>  
#include<cstring>  
#include<algorithm>  
#include<vector>  
#include<fstream>  
using namespace std;  //设点与点之间的距离均为double型  
double INFTY=2147483647;  
const int MAX=1000;  
double dis[MAX][MAX];  
double a[MAX][MAX];  
int path[MAX][MAX];  
int n,m; //结点个数  void Floyd()  
{  int i,j,k;  for(i=1;i<=n;i++)  {  for(j=1;j<=n;j++)  {  dis[i][j]=a[i][j];  if(i!=j&&a[i][j]<INFTY)  {  path[i][j]=i;  }  else  path[i][j]=-1;  }  }  for(k=1;k<=n;k++)  {  for(i=1;i<=n;i++)  {  for(j=1;j<=n;j++)  {  if(dis[i][k]+dis[k][j]<dis[i][j])  {  dis[i][j]=dis[i][k]+dis[k][j];  path[i][j]=path[k][j];  }  }  }  }  
}  int main()  
{  //freopen("datain.txt","r",stdin);  int beg,enda;  double dist;  scanf("%d%d",&n,&m);  for(int i=1;i<=n;i++)  {  for(int j=1;j<=n;j++)  {  if(i==j)  a[i][j]=0;  else  a[i][j]=INFTY;  }  }  for(int i=1;i<=m;i++)  {  scanf("%d%d%lf",&beg,&enda,&dist);  a[beg][enda]=a[enda][beg]=dist;  }  Floyd();  for(int i=1;i<=n;i++)  {  for(int j=1;j<=n;j++)  {  printf("%-12lf",dis[i][j]);  }  printf("\n");  }  return 0;  
}

我是史迪仔，原创不易，如果觉得文章还不错，希望 点赞 支持下，谢谢大家~

欢迎关注公众号【程序员史迪仔】，一起学习交流成长！


http://chatgpt.dhexx.cn/article/ZcSCm5vj.shtml

相关文章

2022数学建模国赛备赛阶段性记录（1-1）

2022数学建模国赛备赛阶段性记录（1-1）

数学建模国赛培训记录&#xff0c;主要使用软件为MATLAB&#xff0c;主要内容为在数学建模竞赛中常用的操作、数学与模型以及部分练习题的解析。 一、常规操作 1、基本运算 MATLAB内四则运算相当于计算机的加减乘除&#xff0c;对应输入数字、运算符&#xff0c;回车即可得出…
阅读更多...
Matlab与数学建模

Matlab与数学建模

一、学习目标。 （1）了解Matlab与数学建模竞赛的关系。 （2）掌握Matlab数学建模的第一个小实例—评估股票价值与风险。 （3）掌握Matlab数学建模的回归算法。 二、实例演练。 1、谈谈你对Matlab与数学建模竞赛的了解。 Matlab在数学建模中使用广泛：MATLAB 是公认的最优秀的数…
阅读更多...
MATLAB在数学建模中的应用

MATLAB在数学建模中的应用

MATLAB在数学建模中的应用 一.预备知识 1.1.关于MATLAB软件 由于科学技术及计算机的飞速发展,各类数学软件不断涌现&#xff0c;这使在解决各类复杂的问题变得非常简单。常用的数学软件有Mathematica、MATLAB、SAS等软件。MATLAB是“Matrix Laboratory"的缩写&#xff…
阅读更多...
数学建模——matlab基本使用

数学建模——matlab基本使用

一&#xff1a;命令窗口两个常用基本命令 清除工作区&#xff1a;clear。清屏&#xff1a;clc。 二&#xff1a;变量与基本运算 圆周率表示&#xff1a;pi。lnx代码化&#xff1a;log(x)。e^x代码化&#xff1a;exp(x) x代表次数。sin(x):sin(x);cos(x):cos(x);tan(x):tan(x…
阅读更多...
MATLAB数学建模-规划模型总结| MATLAB求解

MATLAB数学建模-规划模型总结| MATLAB求解

目录 1 线性规划问题&#xff08;LP&#xff09; 风格1 风格2 2 非线性规划 3 动态规划 A星算法 基于dijkstra的概率路线图 4 多目标规划 帕累托最优 支配&#xff08;Dominace&#xff09; 不可支配解集 帕累托最优解集 帕累托最优前沿面 线性加权法 约束转化法…
阅读更多...
MATLAB--数学建模作图大全及代码说明

MATLAB--数学建模作图大全及代码说明

目录 1、二维曲线 2、二维渐变图 3、二维散点图 4、条形图 5、填充图 6、多Y轴图 7、三维曲线图 8、三维散点图 9、三维伪彩图 10、裁剪伪彩图 11、等高线图 12、三维等高线图 13、等高线填充图 14、三维矢量场图 15、伪彩图投影图 16、热图 17、分子模型图 1…
阅读更多...
如何查询Opencv的版本

如何查询Opencv的版本

环境&#xff1a;Win10 方法&#xff1a; 参考文章上写的很详细&#xff0c;在这里重新编辑一下&#xff0c;保存下来&#xff1a; 1、找到OpenCV的安装主文件夹&#xff0c;在主文件夹中找到“build”文件夹。 2、进入build文件夹以后&#xff0c;在文件夹中找到名为“Ope…
阅读更多...
Linux查看opencv 版本

Linux查看opencv 版本

命令如下&#xff1a; [plain] view plain copy print ? pkg-config --modversion opencv 库文件一般放在&#xff1a; /usr/local/lib &#xff08;PS&#xff0c;系统装的OpenCV版本太多&#xff0c;查找也让人头疼&#xff09; 头文件一般在&#xff1a; /usr/local/inc…
阅读更多...
ubuntu系统下如何查看opencv版本

ubuntu系统下如何查看opencv版本

打开终端&#xff0c;在终端输入&#xff1a; pkg-config --modversion opencv 可以看出&#xff0c;我安装的是opencv 2.4.13版本的。
阅读更多...
在pycharm中查看opencv版本

在pycharm中查看opencv版本

import cv2 print(cv2.__version__)运行后如下图为自己各自安装的版本&#xff1a;
阅读更多...
linux下查看opencv版本

linux下查看opencv版本

直接使用命令 pkg-config --modversion opencv
阅读更多...
opencv查看版本路径

opencv查看版本路径

1、查看ubuntu下的OpenCV安装版本&#xff1a; pkg-config opencv --modversion 2、查看ubuntu的opencv安装路径&#xff1a; sudo find / -iname "*opencv*" 在全盘上不区分大小写&#xff0c;搜索带有关键字opencv的所有文件及文件夹都会输出到终端&#xff0c;如…
阅读更多...
Windows查看OpenCV版本

Windows查看OpenCV版本

打开命令提示符 winr 键打开运行窗口&#xff0c;输入cmd&#xff0c;即可看到弹出的命令提示符窗口输入指令 python import cv2 cv2.__version__得到结果
阅读更多...
http 请求 返回状态码 405 的问题

http 请求 返回状态码 405 的问题

状态码为405表示请求的方式不对&#xff0c; 请求的方式有get、post、head、put…… 常用的为post和get。 代码里面我刚刚开始的时候使用的是HttpPost发的请求&#xff0c;另外一边呢&#xff0c;刚刚开始的时候只有一个get请求在那等着呢。 等我看到405之后&#xff0c;哦&…
阅读更多...
HTTP状态 405 - 方法不允许

HTTP状态 405 - 方法不允许

错误描述&#xff1a; HTTP状态 405 - 方法不允许 类型 状态报告 消息 Request method ‘GET’ not supported 描述 请求行中接收的方法由源服务器知道&#xff0c;但目标资源不支持 此时的原因是请求类型错误&#xff0c;网页是get请求&#xff0c;但是实际上是post请求 解…
阅读更多...
HTTP 405 Method Not Allowed问题的解决

HTTP 405 Method Not Allowed问题的解决

项目中在提交表单时&#xff0c;提示“HTTP 405”错误——“Method Not Allowed” 这里显示的是&#xff0c;方法不被允许。也许经验丰富的开发人员一眼就明了当前的问题。 从字面上的意思理解&#xff0c;很显然是提交方法的类型错误&#xff0c;要么是以GET方式向POST接口提…
阅读更多...
http请求返回405 (Method Not Allowed)

http请求返回405 (Method Not Allowed)

一、问题描述 使用post请求json文件中的数据时&#xff0c;返回报错405(Method Not Allowed) 二、解决方法 由post请求改为get请求&#xff0c;请求静态资源时用get请求&#xff1b; 原因&#xff1a; 使用post请求并且发送的URL是一个具体的资源的时候例如JSON文件, 网站解…
阅读更多...
http 301、302、304、400、405、415状态码解释

http 301、302、304、400、405、415状态码解释

301 moved permanently、302 found、303 see other 301/302/303都表示重定向&#xff0c;所以放在一起讲解。 301表示永久重定向&#xff08;301 moved permanently&#xff09;&#xff0c;表示请求的资源分配了新url&#xff0c;以后应使用新url。 302表示临时性重定向&am…
阅读更多...
http 请求405 错误

http 请求405 错误

问题 postman模拟请求springboot项目&#xff0c;显示台报错 详细问题 解决 由于springboot接口要求以post方式发送请求 对于postman模拟请求应当以post方式发送 原因 405错误表示方法不允许&#xff0c; 多数情况下&#xff0c; 405错误是由于GET,POST,DELETE,PUT等方法…
阅读更多...
页面http 405错误排查

页面http 405错误排查

问题&#xff1a; 这两天pre环境前端发版后&#xff0c;pre就访问不到了&#xff0c;页面会报405错误 分析 HTTP 错误 405 405 不允许此方法 一般是方法是GET你用POST请求了 对于请求所标识的资源&#xff0c;不允许使用请求行中所指定的方法。请确保为所请求的资源设置了正确的…
阅读更多...
推荐文章

Copyright @ 2022~2023